2 ТЕОРЕМАЛАРДЫ ДӘЛЕЛДЕУ. 2.1 Қажетті шартжәне жеткілікті шарттар

2 ТЕОРЕМАЛАРДЫ ДӘ ЛЕЛДЕУ

2. 1 Қ ажетті шартжә не жеткілікті шарттар

Теорема ұ ғ ымы «қ ажетті шарт» жә не «жеткілікті шарт» ұ ғ ымдарымен, ал тура жә не кері теоремалар ұ ғ ымдары, «қ ажетті жә не жеткілікті шарттар» ұ ғ ымдарымен тығ ыз байланысты.

Мектеп математикасында «қ ажет шарттарды», «жеткілікті шарттарды» жә не «қ ажетті жә не жеткілікті шарттарды» қ амтитын теоремалар жиі кездеседі.

1. Егер натурал сан жұ п болса, онда ол 4 – ке бө лінеді.

2. Егер натурал сан 4 – ке бө лінсе, онда ол жұ п сан болады.

3. Егер натурал сан 9 – ғ а бө лінсе, онда ол санның цифрларының қ осындысы 9 – ғ а бө лінеді.

4. Егер натурал санның цифрларының қ осындысы 9 – ғ а бө лінсе, онда ол сан 9 – ғ а бө лінеді.

Осы сө йлемдердің ә рқ айсысы логика тілінде былай жазылады:

1) ;

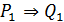2) ;

3) ;

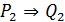4) .

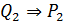Бұ л сө йлемдерді былай да тұ жырымдауғ а болады:

1. Натурал сан жұ п сан болуы ү шін, оның 4 – ке бө лінуі жеткілікті.

2. Натурал сан 4 – ке бө ліну ү шін, оның жұ п сан болуы қ ажетті.

3. Натурал сан 9 – ғ а бө лінуі ү шін, оның цифрларының қ осындысы 9 – ғ а бө лінуі ү шін, сол санның 9 – ғ а бө лінуі қ ажетті жә не жеткілікті.

4. Натурал сан цифрларының қ осындысы 9 – ғ а бө лінуі ү шін, оның сол санның 9 – ғ а бө лінуі қ ажетті жә не жеткілікті.

Осы сө йлемдердеР₁пікірінің ақ иқ ат болуы ү шін, 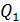пікірі қ ажетті шарт, ал 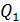пікірінің ақ иқ ат болуы ү шін, Р₁пікірі жеткілікті шарт. пікірінің ақ иқ ат болуы ү шін, Р₂пікірі қ ажетті жә не жеткілікті шарт, осы сияқ ты, Р₂пікірінің ақ иқ ат болуы ү шін, пікірі қ ажеттішарт жә не жеткілікті шарт болып болып табылады.

Жалпы жағ дайда егер 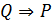ақ иқ ат болса, онда ү шін пікірі қ ажетті шарт деп аталады. Ал егер 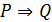ақ иқ ат болса, онда ү шін пікірі жеткілікті шарт деп аталады.

Алайда шарт жеткілікті болып, қ ажетті болмауы жә не керісінше, шарт қ ажетті болмауы жә не керісінше, шарт қ ажетті болып, жеткілікті болмауы да мү мкін. Мә селен,

1) Мысалда Р₁ – дің ақ иқ аттығ ынан 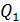– дің ақ иқ аттығ ы шығ ады, бірақ 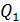– дің ақ иқ аттығ ы басқ а бір Р₃ шарттан да шығ уы мү мкін. Мысалы, натурал сан жұ п болу ү шін 4 – ке немесе 2 – ге, болмаса 6 – ғ а бө лінуі жеткіліксіз;

2) Мысалды Р₁ – дің ақ иқ аттығ ынан 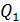– дің ақ иқ аттығ ы шығ ады жә не де 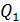ақ иқ ат болғ анымен, Р₁ жаллғ ан болуы да мү мкін. Мә селен, натурал сан 4 – ке бө ліну ү шін, оның ижұ п сан болуы қ ажетті, бірақ жеткіліксіз, ө йткені 10 – жұ п сан болғ анымен, 4 – ке бө лінбейді.

Оқ ушылардың материалды жете тү сінуіне қ иындық туғ ызатын ұ ғ ымдардың бірі–қ ажеттіжә нежеткіліктішарттар. Егер 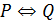эквиваленттік шарты ( 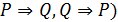орындалса, онда Р шарты ү шін қ ажетті жә не жеткілікті деп атайды. «Егер натурал санның цифрларының қ осындысы 9 – ғ а бө лінсе, ол сан 9 – ғ а бө лінеді деген сө йлем қ ажетті жә не жеткілікті шартты білдіреді.

Қ ажетті жә не жеткілікті шарттың ө зі, тура теорема мен оғ ан кері теореманың дұ рыстығ ын кө рсетеді. Сондай – ақ, керісінше, тура жә не кері теоремалардың дұ рыстығ ы қ ажетті жә не жеткілікті шарттарды тағ айындауғ а мү мкіндік береді.

Трапецияның ө зімізге белгілі аныұ тамасын қ арастырайық: «Трапеция деп қ арама – қ арсы екі қ абырғ асы параллель тө ртбұ рышты айтады».

Осы анық тамадан трапецияның қ асиетін кө рсететін мынадай тұ жырымдар жасауғ а болады:

1. Трапецияның тө рт тө бесі бар;

2. Трапецияның тө рт бұ рышы бар;

3. Трапецияның параллель екі қ абырғ асы бар.

Дегенмен, трапецияның алғ ашқ ы екі қ асиеті тө ртбұ рыштардың басқ а

тү рлеріне де тә н. Ал ү шінші қ асиеті тек трапецияны ғ ана сипаттайды.

Математикалық ұ ғ ымның мұ ндай қ асиеті оның сипаттық (характеристикалық ) қ асиеті деп атайды.

Трапецияны былай да анық тауғ а болады: «Екі қ абырғ асы ө зара параллель тө ртбұ рыш қ ана трапеция болады». Тек екі қ абырғ асының параллельдігі мен тө рт қ абырғ асы болу қ асиеті трапеция ұ ғ ымын толық сипаттауғ а қ ажетті, ал оның қ асиеттерінің жоғ арыда келтірілген тізімі жеткілікті шарттар.

Сонымен бірге, белгілі бір ұ ғ ымды толық сипаттайтын қ асиеттер берілген ұ ғ ымғ а тә н қ асиеттердің тізімінен ә р алуан тә сілдермен іріктеліп алынады. Егер ұ ғ ым қ асиеттерінің бір тобы оның анық тамасының негізін қ аласа, енді бір тобы оның анық тамысының негізін қ аласа, енді бір тобы теорема тү рінде кө рінеді. Ұ ғ ымның бар болуының жеткілікті шартын кө рсететін теоремалар осы ұ ғ ымның белгі – теоремаларыдеп аталады, ал ұ ғ ымның бар болуының қ ажетті шартын кө рсететін теоремалар осы ұ ғ ымның бар болуының қ ажетті шартын кө рсететін теоремалар осы ұ ғ ымның қ асиет – теоремалары деп аталады.

Қ орыта келгенде, А анық тамасымен ө рнектелген Ғ фигурасы (объектісі) 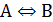орындалатындай, В қ асиетіне ие болса, онда Вқ асиеті Ғ фигурасының (объектісінің ) сипаттық қ асиеті болып табылады. Кез – келген математикалық математикалық объектінің сипаттық қ асиетін осы объектінің анық тамасы ретінде қ абылдауғ а болады.

Мысалы, «Тік бұ рышты ү шбұ рыштың екі сү йір бұ рышының қ осындысы тік бұ рышқ а тең » теоремасы тік бұ рышты ү шбұ рыштың қ айсыбір қ асиетін ғ ана кө рсетеді. Ал: « Егер ү шбұ рыштың екі ішкі бұ рышының қ осындысы ү шінші бұ рышына тең болса, онда ол ү шбұ рыш тік бұ рышты ү шбұ рыш болады » теоремасы – тік бұ рышты ү шбұ рышты толық анық тайтын қ асиетін, яғ ни ондай ү шбұ рыштың бар болуын кө рсететін белгі.

Қ ажетті жә не жеткілікті шарттар есеп шығ ару барысында да жиі кездеседі. Сондық тан бұ л ұ ғ ымдарды оқ ушылардың жете мейгеруіне мұ ғ алімнің баса назар аударғ аны жө н.

⇐ Предыдущая 1 2 345 6 Следующая ⇒