
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Решение
Решение
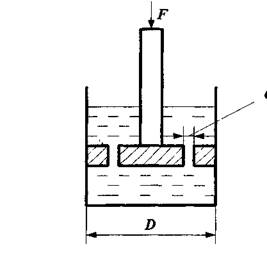 1-
1- 
Рабочую площадь поршня найдем по формуле:
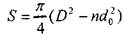
тогда давление поршня на жидкость в нижней полости будет равно:
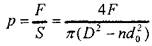
Если давление в жидкости на верхней плоскости поршня равно р0, то давление на нижней плоскости поршня будет равно р0 + ρ , т. е. перепад давлений по длине отверстия будет равен ρ . Тогда расход через одно отверстие можно найти по формуле:
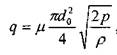
а суммарный расход через n отверстий

|
Пусть поршень двигается с постоянной скоростью υ. Тогда за интервал времени
τ объем жидкости под поршнем изменится на величину
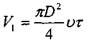
|
За это же время через отверстия перетечет объем жидкости равный V2 = Q τ . Из равенства
V1=V2 получим
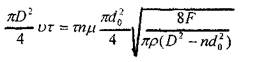
из этого равенства найдем скорость поршня
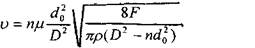
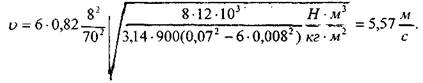
Ответ: V= 5, 57 
Задача 7
Центробежный насос (рис. 7. 1) откачивает воду из сборного колодца в резервуар с постоянным уровнем H по трубопроводам размерами l1, d1 и l2, d2.
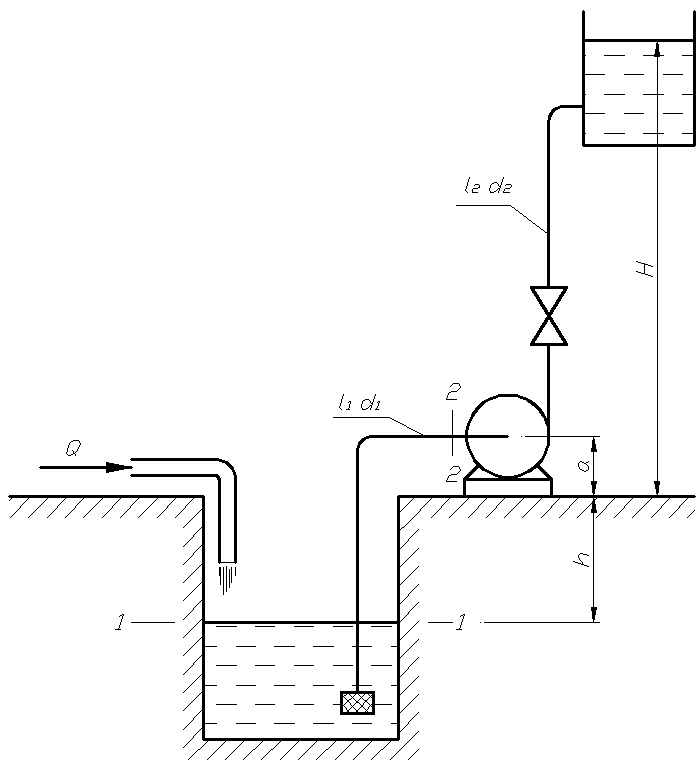
Рис. 7. 1
Эквивалентная шероховатость поверхности труб ∆, плотность воды ρ =1000 кг/м3, кинематический коэффициент вязкости ν = 0, 01 см2/с, расстояние a = 1 м.
Характеристики насоса представлены следующими параметрами:
| Q, л/с | |||||||||||
| Hн, м | 47, 5 | 48, 5 | 22, 5 | ||||||||
| Hвакдоп, м | - | - | 8, 2 | 7, 6 | 6, 6 | 5, 5 | 4, 75 |
При расчетах принять суммарные коэффициенты местных сопротивлений на всасывающей линии ζ 1=10, на напорной линии ζ 2=6.
Требуется определить:
1. На какой глубине h установится уровень воды в колодце, если приток в него Q?
2. Вакуумметрическую высоту всасывания при входе в насос Hвак, выраженную в метрах водяного столба (м в. ст. ).
3. Максимальную допустимую геометрическую высоту всасывания при заданном расходе.
| Исходные данные | Вариант№3 |
| H, м | |
| l1, м | |
| l2, м | |
| d1, мм | |
| d2, мм | |
| ∆, мм | 0, 5 |
| Q, л/с |
Решение.
1. При заданном расходе 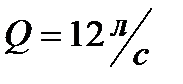 величины
величины 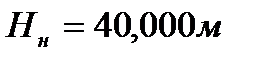 и
и 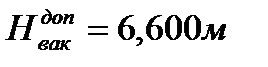 .
.
2. Напор, развиваемый насосом, расходуется на подъем воды на геометрическую высоту 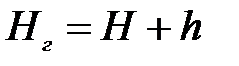 и преодоление потерь напора во всасывающей и нагнетательной линиях:
и преодоление потерь напора во всасывающей и нагнетательной линиях:
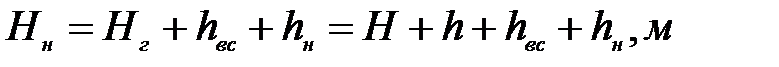 (7. 1)
(7. 1)
откуда искомая величина
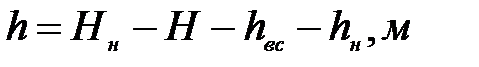 (7. 2)
(7. 2)
где 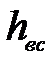 - потери напора во всасывающей линии,
- потери напора во всасывающей линии, 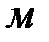 ;
;
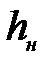 - потери напора в нагнетательной линии,
- потери напора в нагнетательной линии, 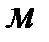 .
.
3. Потери напора во всасывающей линии определяются как сумма местных потерь напора и потерь напора по длине трубопровода:
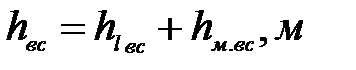 (7. 3)
(7. 3)
где 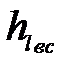 - потери напора по длине во всасывающей линии, определяются по формуле Вейсбаха - Дарси:
- потери напора по длине во всасывающей линии, определяются по формуле Вейсбаха - Дарси:
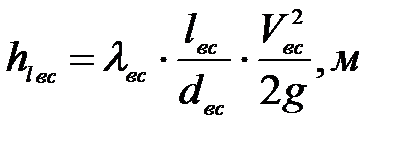 (7. 4)
(7. 4)
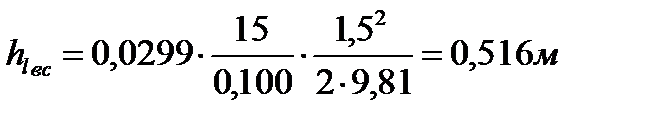
где 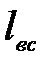 - длина всасывающей трубы,
- длина всасывающей трубы, 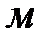 ;
;
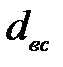 - диаметр всасывающей трубы,
- диаметр всасывающей трубы, 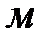 ;
;
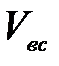 - средняя скорость движения воды во всасывающей трубе,
- средняя скорость движения воды во всасывающей трубе, 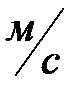 ;
;
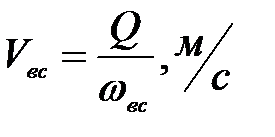 (7. 5)
(7. 5)
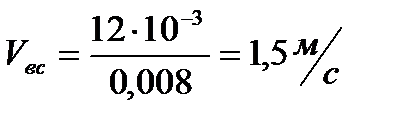
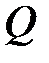 - расход воды во всасывающей линии,
- расход воды во всасывающей линии,  ;
;
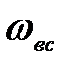 - площадь живого сечения всасывающей трубы,
- площадь живого сечения всасывающей трубы, 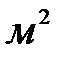 ;
;
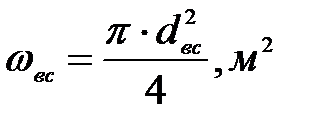 (7. 6)
(7. 6)
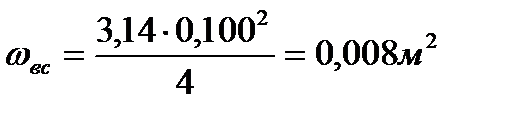
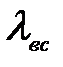 - гидравлический коэффициент трения во всасывающей линии, определяется по формуле Альтшуля:
- гидравлический коэффициент трения во всасывающей линии, определяется по формуле Альтшуля:
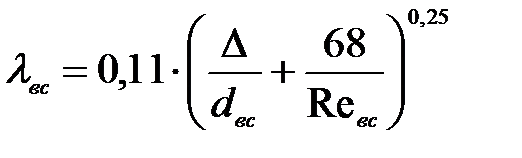 (7. 7)
(7. 7)
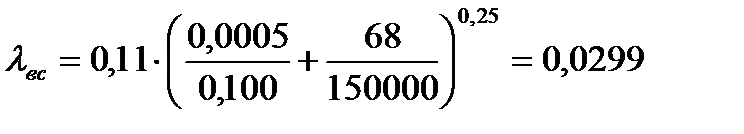
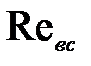 - число Рейнольдса на участке всасывающей трубы;
- число Рейнольдса на участке всасывающей трубы;
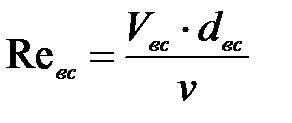 (7. 8)
(7. 8)
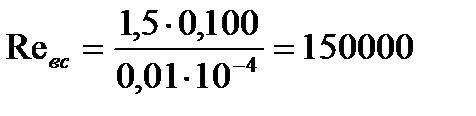
 - эквивалентная шероховатость поверхности труб,
- эквивалентная шероховатость поверхности труб, 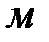 ;
;
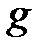 - ускорение свободного падения,
- ускорение свободного падения, 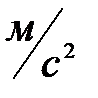 ;
;
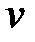 - кинематический коэффициент вязкости,
- кинематический коэффициент вязкости, 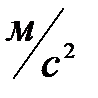 ;
;
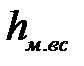 - потери напора в местных сопротивлениях,
- потери напора в местных сопротивлениях, 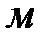 ;
;
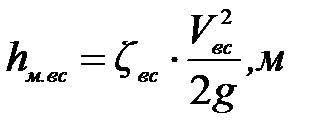 (7. 9)
(7. 9)
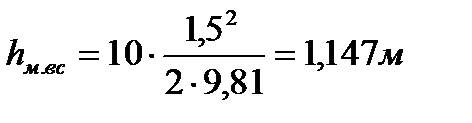
где 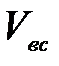 - средняя скорость движения воды во всасывающей трубе,
- средняя скорость движения воды во всасывающей трубе, 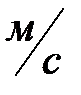 ;
;
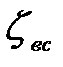 - суммарный коэффициент местных сопротивлений на всасывающей линии.
- суммарный коэффициент местных сопротивлений на всасывающей линии.
Подставляя полученные значения в формулу (7. 3) определяем потери напора во всасывающей линии
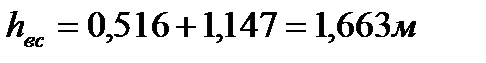
4. Потери напора в нагнетательной (напорной) линии определяются как сумма местных потерь напора и потерь напора по длине трубопровода:
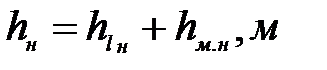 (7. 10)
(7. 10)
где 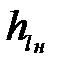 - потери напора по длине в нагнетательной линии, определяются по формуле Вейсбаха - Дарси:
- потери напора по длине в нагнетательной линии, определяются по формуле Вейсбаха - Дарси:
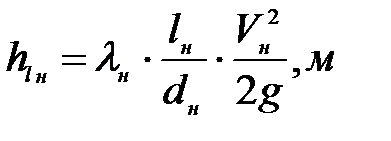 (7. 11)
(7. 11)
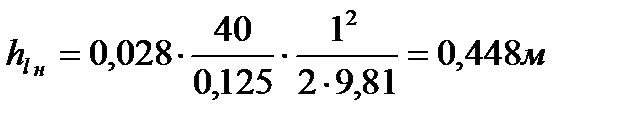
где 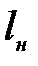 - длина нагнетательной трубы,
- длина нагнетательной трубы, 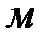 ;
;
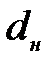 - диаметр нагнетательной трубы,
- диаметр нагнетательной трубы, 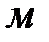 ;
;
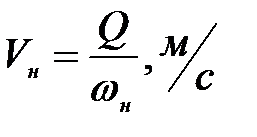 (7. 12)
(7. 12)
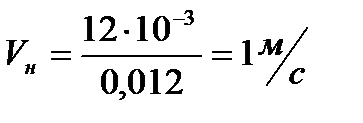
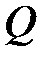 - расход воды в нагнетательной линии,
- расход воды в нагнетательной линии, 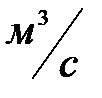 ;
;
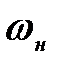 -площадь живого сечения нагнетательной линии,
-площадь живого сечения нагнетательной линии,  ;
;
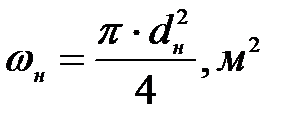 (7. 13)
(7. 13)
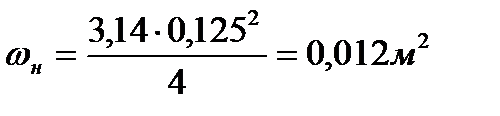
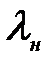 - гидравлический коэффициент трения в нагнетательной линии, определяется по формуле Альтшуля:
- гидравлический коэффициент трения в нагнетательной линии, определяется по формуле Альтшуля:
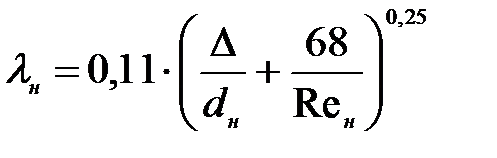 (7. 14)
(7. 14)
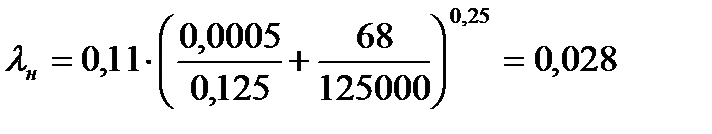
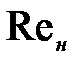 - число Рейнольдса на участке нагнетательной линии;
- число Рейнольдса на участке нагнетательной линии;
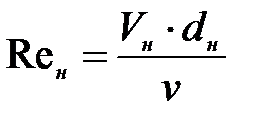 (7. 15)
(7. 15)
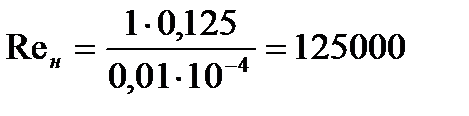
 - эквивалентная шероховатость поверхности труб,
- эквивалентная шероховатость поверхности труб, 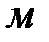 ;
;
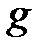 - ускорение свободного падения,
- ускорение свободного падения, 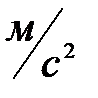 ;
;
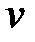 - кинематический коэффициент вязкости,
- кинематический коэффициент вязкости, 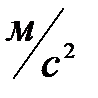 ;
;
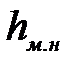 - потери напора в местных сопротивлениях в нагнетательной линии,
- потери напора в местных сопротивлениях в нагнетательной линии, 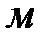 ;
;
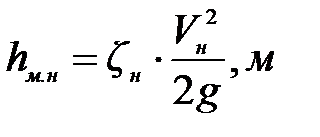 (7. 16)
(7. 16)
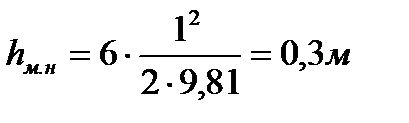
где 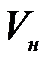 - средняя скорость движения воды в нагнетательной линии,
- средняя скорость движения воды в нагнетательной линии, 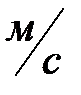 ;
;
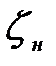 - суммарный коэффициент местных сопротивлений в нагнетательной линии.
- суммарный коэффициент местных сопротивлений в нагнетательной линии.
Подставляя полученные значения в формулу (7. 10) определяем потери напора в нагнетательной (напорной) линии
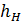 =0, 448 + 0, 3 = 0, 748 м
=0, 448 + 0, 3 = 0, 748 м
Подставляя полученные значения в формулу (7. 2) определяем какой глубине 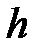 установится уровень воды в колодце
установится уровень воды в колодце
h= 40-33-1, 663-0, 748=4, 589 м
5. Вакуумметрическую высоту всасывания при входе в насос определяем из уравнения Бернулли, составленного для сечений 1-1 и 2-2, приняв за горизонтальную плоскость сравнения сечение 1-1:
 (7. 17)
(7. 17)
где 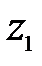 - геометрическая высота сечения 1-1 над плоскостью сравнения,
- геометрическая высота сечения 1-1 над плоскостью сравнения, 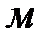 . Так как плоскость сравнения проведена по сечению 1-1, то
. Так как плоскость сравнения проведена по сечению 1-1, то 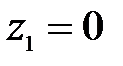 ;
;
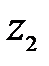 - геометрическая высота сечения 2-2 над плоскостью сравнения,
- геометрическая высота сечения 2-2 над плоскостью сравнения, 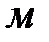 . Так как плоскость сравнения проведена по сечению 1-1, то
. Так как плоскость сравнения проведена по сечению 1-1, то 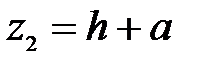 ;
;
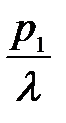 - пьезометрическая высота в сечении 1-1, так как на свободную поверхность воды в резервуаре действует атмосферное давление, то
- пьезометрическая высота в сечении 1-1, так как на свободную поверхность воды в резервуаре действует атмосферное давление, то 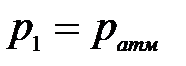 , то есть
, то есть 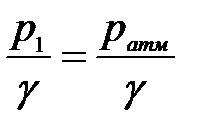 ;
;
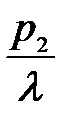 - пьезометрическая высота в сечении 2-2, так как давление перед насосом составляет
- пьезометрическая высота в сечении 2-2, так как давление перед насосом составляет 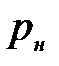 ,
, 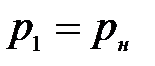 , то есть
, то есть 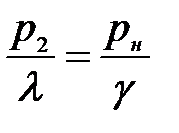 ;
;
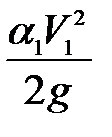 - скоростная высота в сечении 1-1, так как скорость на поверхности резервуара считается равной 0, то
- скоростная высота в сечении 1-1, так как скорость на поверхности резервуара считается равной 0, то 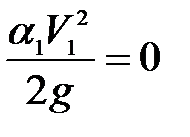 ;
;
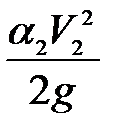 - скоростная высота в сечении 2-2, так как скорость перед насосом составляет
- скоростная высота в сечении 2-2, так как скорость перед насосом составляет 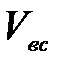 , а коэффициент Кориолиса
, а коэффициент Кориолиса 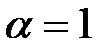 , то
, то  ,
, 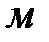 ;
;
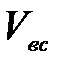 - средняя скорость движения воды во всасывающей линии,
- средняя скорость движения воды во всасывающей линии, 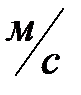 ;
;
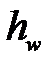 - потери напора во всасывающей линии,
- потери напора во всасывающей линии, 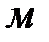 ,
, 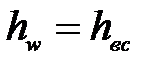 .
.
Подставляя найденные члены уравнения Д. Бернулли, получаем:
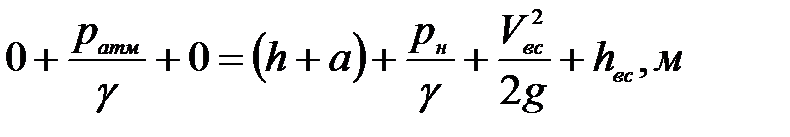 (7. 18)
(7. 18)
Как известно, вакуум - это недостаток абсолютного давления до атмосферного, то есть 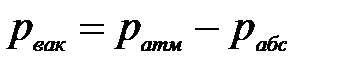 , тогда величина вакуума перед насосом будет равна:
, тогда величина вакуума перед насосом будет равна:
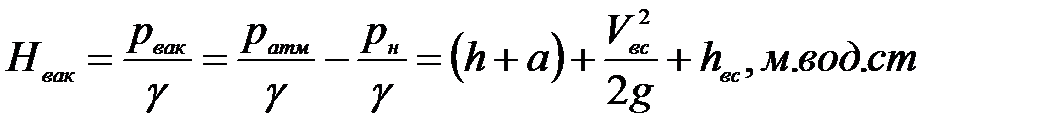 (7. 19)
(7. 19)
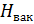 =(4, 589+1)+
=(4, 589+1)+ 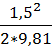 +1, 663=7, 362 м. вод. ст
+1, 663=7, 362 м. вод. ст
или в Паскалях:
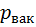 =
= 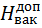 *
* 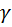 , Па (7. 20)
, Па (7. 20)
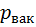 =6, 6*9810 = 64746 Па
=6, 6*9810 = 64746 Па
где 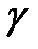 - вес единицы объема жидкости,
- вес единицы объема жидкости, 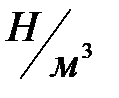 ;
;
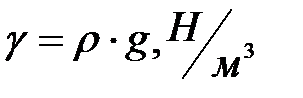 (7. 21)
(7. 21)
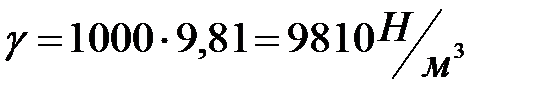
6. Максимальная допустимая геометрическая высота всасывания при заданном расходе определяется по формуле:
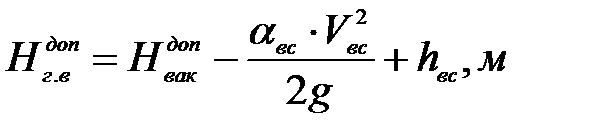 (7. 22)
(7. 22)
где 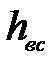 - потеря напора во всасывающей линии,
- потеря напора во всасывающей линии, 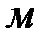 ;
;
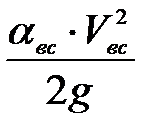 - скоростной напор во всасывающей линии при заданном расходе,
- скоростной напор во всасывающей линии при заданном расходе, 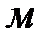 ;
;
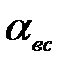 - коэффициент кинетической энергии потока (принимаем
- коэффициент кинетической энергии потока (принимаем 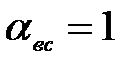 );
);
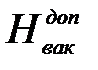 - допустимая вакуумметрическая высота всасывания, определяем по графику,
- допустимая вакуумметрическая высота всасывания, определяем по графику,  ;
;
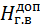 = 6, 6 -
= 6, 6 - 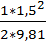 + 1, 663 = 8, 153 м.
+ 1, 663 = 8, 153 м.
Ответ: h=4, 589 м, 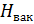 =7, 362 м. вод. ст,
=7, 362 м. вод. ст, 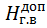 =8, 153 м.
=8, 153 м.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|