
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Задача 5
Задача 5
К системе, состоящей из двух параллельно соединённых трубопроводов, имеющих длины соответственно l1 и l2 и диаметры d1 и d2 (коэффициент шероховатости n = 0, 012), подводится к точке A вода, расход которой Q
(рис. 5. 1).
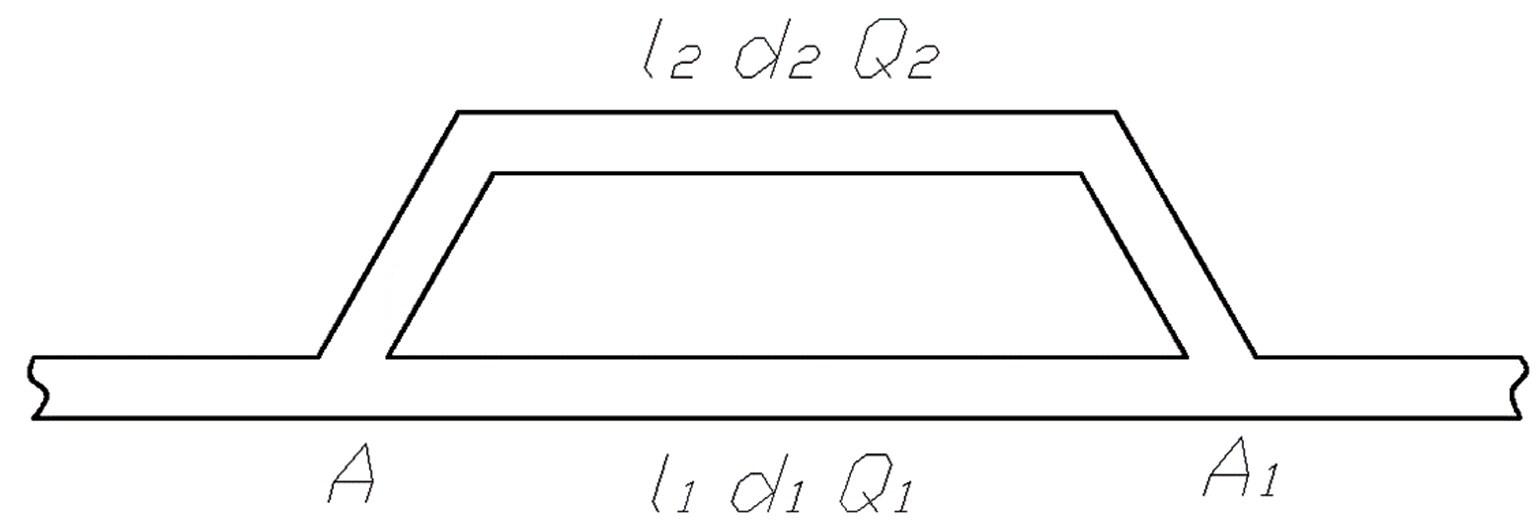
Рис. 5. 1
Требуется определить потерю напора на участке AA1 и величины расходов воды на каждом участке.
| Исходные данные | Вариант № 3 | |
|
| ||
| Q, л/с | ||
| l1, м | ||
| d1, мм | ||
| l2, м | ||
| d2, мм | ||
Решение
Потери напора на каждом из двух параллельно соединённых трубопроводов одинаковы:
hl1 = hl2 = hl (5. 1)
где hl1 и hl2 – потери напора по длине соответственно на первом и втором
трубопроводах.
Порядок расчета:
1. По формуле (5. 2) определить модули расхода для первого и второго трубопровода
K =ω ⋅ C ⋅ 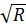 (5. 2)
(5. 2)
где ω – площадь живого сечения;
С – коэффициент Шези;
R =ω / 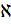 –гидравлический радиус;
–гидравлический радиус; 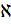 -смоченный периметр.
-смоченный периметр.
В случае напорного трубопровода χ = π d. Коэффициент Шези вычислить по формуле Маннинга
C= 
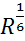 (5. 3)
(5. 3)
где n – коэффициент шероховатости.
Для первого трубопровода:
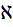 =
= 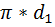 = 3, 14*0, 25= 0, 79 м
= 3, 14*0, 25= 0, 79 м
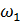 =
= 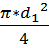 =
= 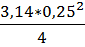 =0, 05
=0, 05 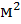
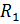 =
= 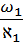 =
= 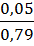 =0, 06 м
=0, 06 м
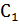 =
=  *
* 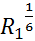 =
= 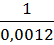 *
* 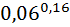 =53, 33
=53, 33
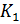 =
= 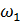 *
* 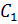 *
* 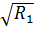 = 0, 05*53, 33*0, 24=0, 64
= 0, 05*53, 33*0, 24=0, 64 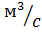
Для второго трубопровода:
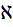 =
= 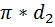 = 3, 14*0, 3= 0, 94 м
= 3, 14*0, 3= 0, 94 м
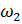 =
= 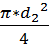 =
= 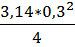 =0, 07
=0, 07 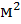
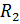 =
= 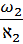 =
= 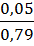 =0, 07 м
=0, 07 м
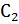 =
=  *
* 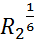 =
= 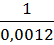 *
* 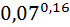 =54, 16
=54, 16
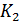 =
= 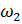 *
* 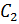 *
* 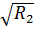 = 0, 07*54, 16*0, 26=0, 7
= 0, 07*54, 16*0, 26=0, 7 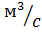
2. Используя зависимость (5. 4) вычислить потерю напора на участке AA1
hl= 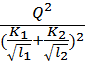 = (5. 4)
= (5. 4)
= 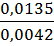 = 3, 21 м
= 3, 21 м
3. Определить расходы в каждом из трубопроводов
Q1 = 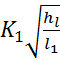 =0, 64*
=0, 64* 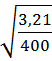 = 0, 06
= 0, 06 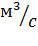 (5. 5)
(5. 5)
Q2 = Q – Q1 = 0, 116-0, 06=0, 056 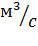 (5. 6)
(5. 6)
4. Вычислим потери напора на каждом из параллельных участков А 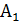 :
:
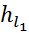 =
= 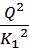 *
* 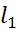 =
= 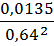 *400
*400 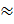 13 м
13 м
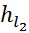 =
= 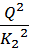 *
* 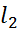 =
= 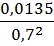 *450
*450 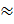 13 м
13 м
Ответ: 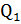 =0, 06
=0, 06 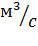 ;
; 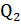 =0, 056
=0, 056 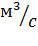 ;
; 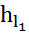 =
= 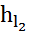 =13 м
=13 м
Задача № 6
Поршень диаметром D имеет n отверстий диаметром d0каждое (рис. 6. 1). Отверстия рассматривать как внешние цилиндрические насадки с коэффициентом расхода µ = 0, 82; плотность жидкости ρ = 900 кг/м3.
Требуется определить скорость v перемещения поршня вниз, если к его штоку приложена сила F.
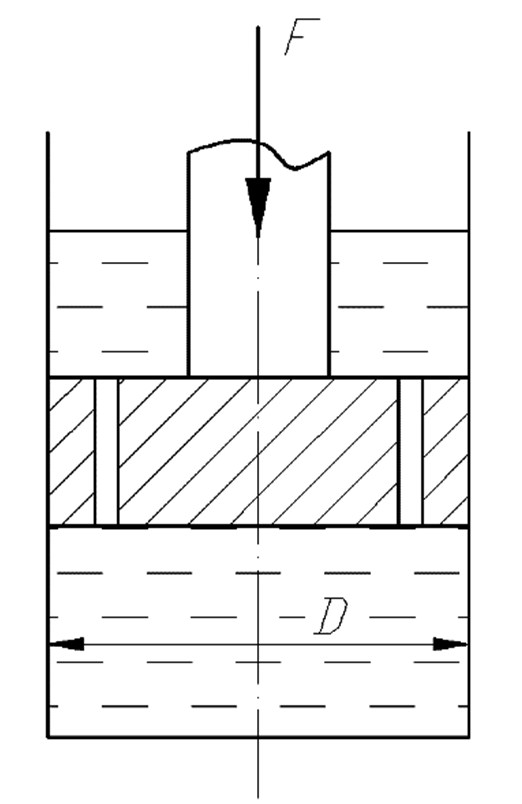
Рис. 6. 1
| Исходные данные. | D, мм | 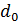 , мм , мм
| n | F, кН |
| Вариант№ 3 |
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|