
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Задача 2
Задача 2
В вертикальном цилиндрическом резервуаре, имеющем диаметр D, хранится нефть, вес её G, плотность ρ = 850 кг/м3, коэффициент температурного расширения β t = 0, 00072 1/°С. Расширение стенок резервуара не учитывается.
Требуется определить:
1. Объём нефти в резервуаре при температуре 0 °С.
2. Изменение уровня нефти в резервуаре, если температура повысится на Т, °С
| Исходные данные | Вариант №3 |
| D, м | |
| G, кН | 2000 |
| Т, °С |
Решение.
1. Объём нефти в резервуаре при температуре 0 °С:
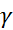 =
= 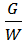 , удельный вес жидкости в единице объёма
, удельный вес жидкости в единице объёма
Плотность и удельный вес связаны между собой известным соотношением:
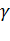 =
= 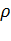 *g, где g - ускорение свободного падения и равно 9, 81 м/
*g, где g - ускорение свободного падения и равно 9, 81 м/ 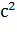 , значит
, значит
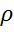 *g =
*g = 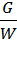 , отсюда
, отсюда
W= 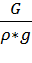 =
= 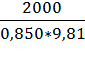 = 240, 09
= 240, 09 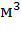
2. Изменение уровня нефти в резервуаре, если температура повысится на 40°С:
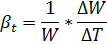
Значит:
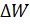 =
= 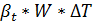 =0, 00072*240, 09*40=6, 91
=0, 00072*240, 09*40=6, 91 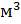
Ответ: W=240, 09 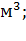
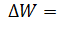 6, 91
6, 91 
Задача 3
Круглый горизонтальный резервуар (рис. 3. 1), имеющий диаметр D и длину L, заполнен жидкостью, плотность которой ρ. Манометр, установленный на уровне верхней образующей, показывает избыточное давление p.
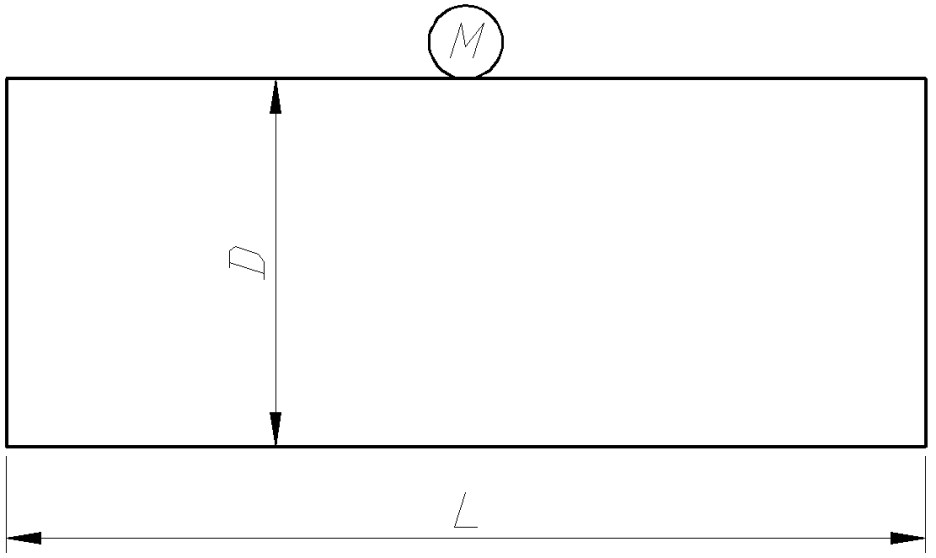
Рис. 3. 1
Требуется определить:
1. Горизонтальную силу гидростатического давления Px, действующую на круглый торец резервуара.
2. Расстояние e, на которое отстоит линия действия горизонтальной силы от оси резервуара.
3. Вертикальную силу Pz, действующую на верхнюю половину резервуара.
| Исходные данные | Вариант№ 3 |
| D, м | 2, 5 |
| p, МПа | 0, 04 |
| ρ, кг/м3 | 850 |
| L, м | 6 |
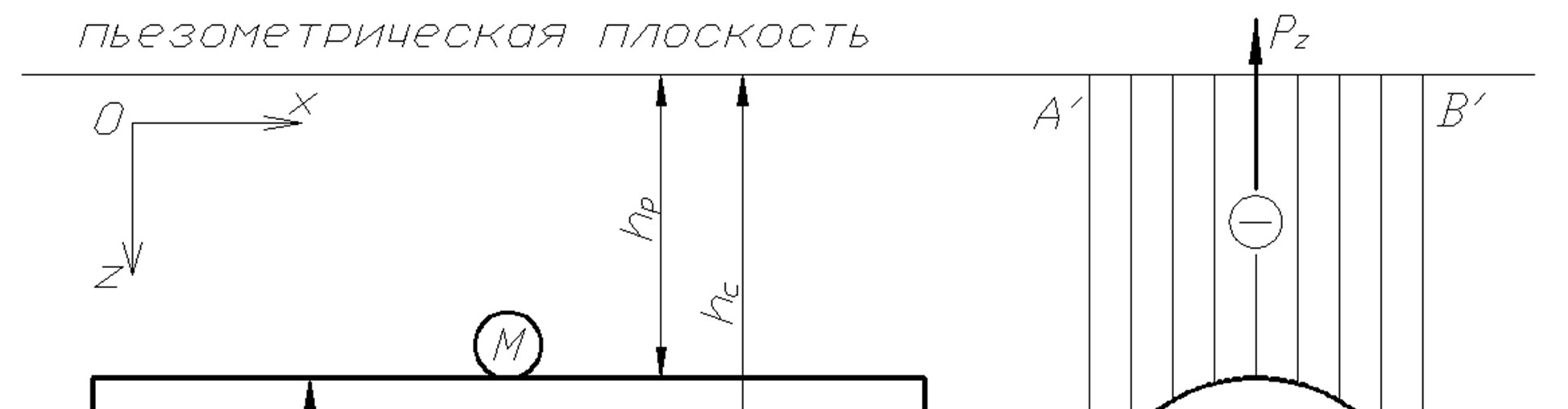
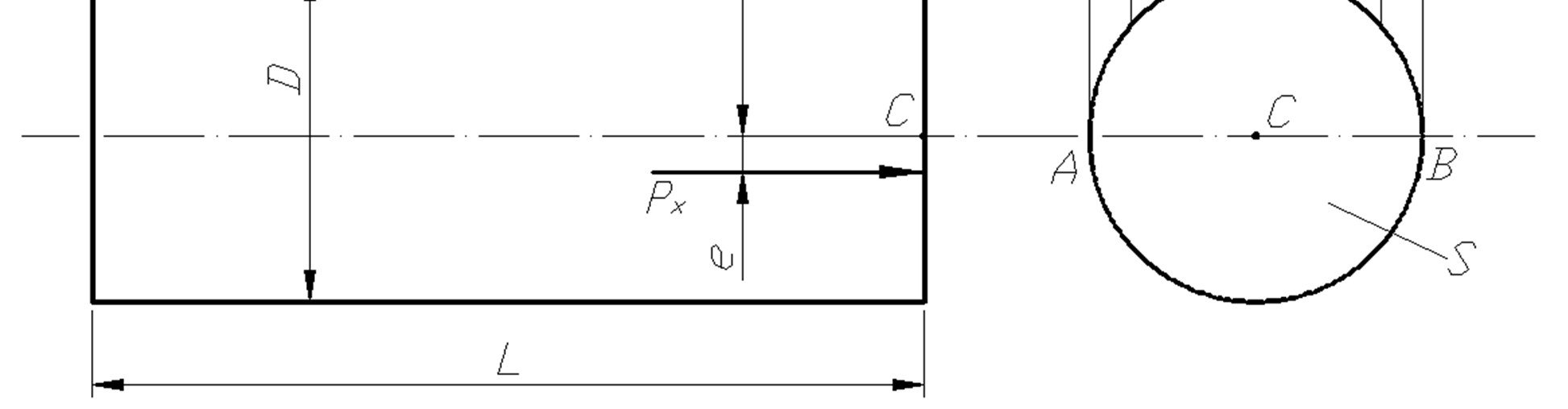
Рис. 3. 2
Решение:
1. Поскольку избыточное давление равно p, Па, то пьезометрическая поверхность будет находится выше места присоединения манометра на величину:
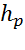 =
= 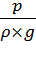 =
= 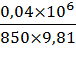 = 4, 79
= 4, 79 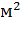 ,
,
где g-ускорение свободного падения= 9, 81 м/ 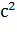
2. Определяем горизонтальную силу гидростатического давления 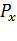 действующую на круглый торец резервуара:
действующую на круглый торец резервуара:
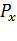 = P =
= P = 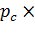 S=
S= 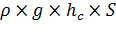 , МПа
, МПа
где 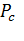 избыточное гидростатическое давление в центре тяжести торцевой стенки резервуара площадью S:
избыточное гидростатическое давление в центре тяжести торцевой стенки резервуара площадью S:
S- площадь круглого торца резервуара, 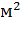
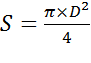 =
= 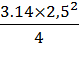 = 4, 9
= 4, 9 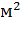
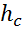 - глубина погружения центра тяжести рассматриваемой плоской фигуры под пьезометрической поверхностью. (расстояния от центра тяжести плоской фигуры до ПП).
- глубина погружения центра тяжести рассматриваемой плоской фигуры под пьезометрической поверхностью. (расстояния от центра тяжести плоской фигуры до ПП).
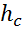 =
= 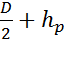 = 1, 25 + 4. 79= 6. 04 м.
= 1, 25 + 4. 79= 6. 04 м.
Значит 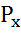 = 850*9, 81*6, 04*4, 9=246786, 24 =247, 8 кН
= 850*9, 81*6, 04*4, 9=246786, 24 =247, 8 кН
3. Линии действия силы 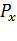 находится ниже центра тяжести плоской фигуры на величину е (эксцентрисистет):
находится ниже центра тяжести плоской фигуры на величину е (эксцентрисистет):
е = 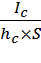 , м
, м
где 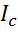 – центральный момент инерции фигуры S относительно горизонтальной оси. Для круга диаметром D=2, 5 м:
– центральный момент инерции фигуры S относительно горизонтальной оси. Для круга диаметром D=2, 5 м:
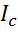 =
= 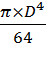 =
= 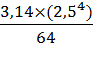 = 1, 92
= 1, 92
Значит е= 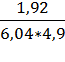 =0, 07 м
=0, 07 м
4. Вертикальная сила, действующая на верхнюю половину резервуара рассчитывается по формуле:
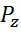 =
= 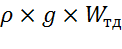 , Н
, Н
где 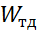 – объём тела давления.
– объём тела давления.
Телом давления называют объём, ограниченный сверху пьезометрической поверхностью, снизу- криволинейной цилиндрической поверхностью, с боков вертикальными линиями, проведенными из краев криволинейной поверхности до ПП.
Чтобы получить объём тела давления 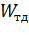 нужно площадь поперечного сечения тела давления
нужно площадь поперечного сечения тела давления 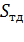 (на рис. 3. 2 заштрихован) умножить на длину резервуара. Площадь поперечного сечения тела давления считается по формуле:
(на рис. 3. 2 заштрихован) умножить на длину резервуара. Площадь поперечного сечения тела давления считается по формуле:
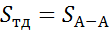 -
- 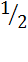 S,
S,
где 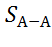 =D
=D 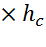 =2, 5*6, 04= 15, 1м
=2, 5*6, 04= 15, 1м
S= 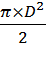 =
= 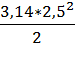 =9, 8
=9, 8 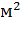
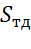 =15, 1 -
=15, 1 - 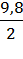 = 10, 2
= 10, 2 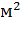
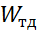 =
= 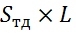 = 10, 2*6 = 61, 2
= 10, 2*6 = 61, 2 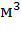
Значит 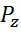 =850*9, 81*61, 2= 510316, 2=510, 3 кН
=850*9, 81*61, 2= 510316, 2=510, 3 кН
Так как жидкость и тело давления расположены по разные стороны от криволинейной поверхности, то вертикальная сила 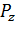 направленна вверх.
направленна вверх.
Ответ : 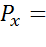 247, 8 кН
247, 8 кН 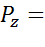 510, 3 кН e =0, 07 м
510, 3 кН e =0, 07 м
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|