Хелпикс

Главная

Контакты

Случайная статья



Варіант 21

⇐ ПредыдущаяСтр 22 из 31Следующая ⇒


 

1. Знайдіть і зобразіть область визначення функції

а) ;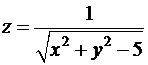

б) .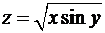

2. Обчисліть значення частинних похідних функції 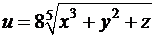 у точці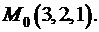  

3. Знайдіть повний диференціал функції

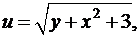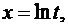
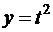4. Обчисліть значення похідної складеної функції  де  при .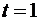

5. Знайдіть 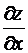 та 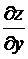, якщо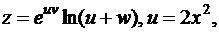

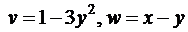
6. Для функції 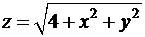, точки  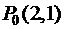та вектора  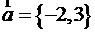знайдіть  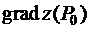і .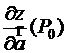

7. Обчисліть наближено .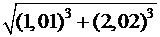

8. Доведіть, що функція 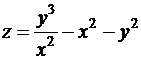 задовольняє рівняння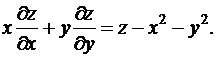

9.  Дослідіть на екстремум функцію .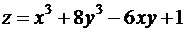

10. Знайдіть умовний екстремум функції 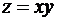   при .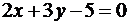

11. Знайдіть найбільше і найменше значення функції 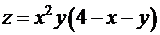 в заданій області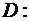

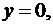
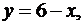
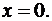
Знайдіть загальний розв’язок (загальний інтеграл) диференціального рівняння.

12. .

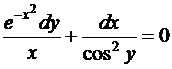13. .

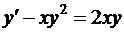14. .

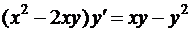15.  Знайдіть частинний розв’язок (частинний інтеграл) диференціального рівняння

 , .

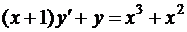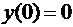16. Знайдіть загальний розв’язок диференціального рівняння .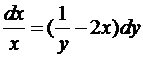

Знайдіть загальний розв’язок диференціального рівняння

17. a) ;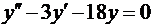      

б) ;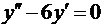

в) .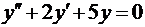

18. .

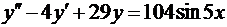19. .

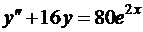20.  Знайдіть частинний розв’язок диференціального рівняння, що задовольняє початкові умови.

, .

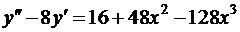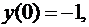
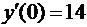21. Дослiдіть збіжність ряду 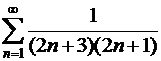  і знайдіть його суму.

Дослідіть на збіжність ряди з додатними членами

22. .  

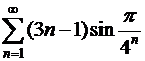23. .

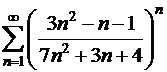24.. .

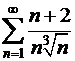25. Дослідіть на збіжність і абсолютну збіжність знакопочерговий ряд .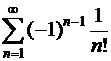

26. Знайдіть область збіжності функціональних рядів

а) ;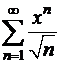       

б) .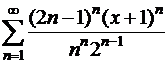

27.  Запишіть ряд Маклорена функції 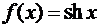. Вкажіть область збіжності отриманого ряду до цієї функції.

28. Користуючись розкладом у степеневий ряд відповідно підібраної функції, обчисліть 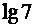  із заданою точністю .

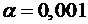29. Розвиньте у ряд Фур’є періодичну з періодом 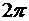 функцію 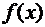, задану на інтервалі .

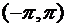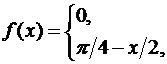
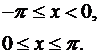
30. Розвиньте у ряд Фур’є періодичну з періодом 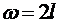 функцію

, .

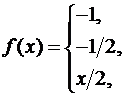
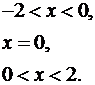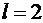31. Розвиньте у ряд Фур’є за косинусами функцію 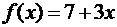, задану на відрізку .


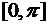⇐ Предыдущая17181920212223242526Следующая ⇒
  

© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.