Задача 1.7

Задача 1.7

Трубопровод тепловой магистрали диаметром 20 см защищен изоляцией толщиной 10 см. Величина коэффициента теплопроводности изоляции k=0,00017, температура трубы 160 ºС. Температура внешнего покрова изоляции 30 ºС. Найти распределение температуры внутри изоляции, а также количество тепла, отдаваемого 1 пог. м трубы. Расчетная схема изображена на рисунке 1.4.

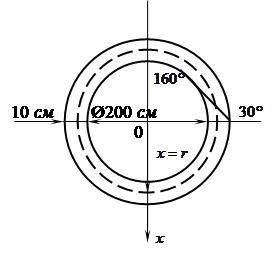
Рисунок 1.4 — Схема расчета распределения температуры внутри изоляции

трубопровода к задаче 1.7

Если тело находится в стационарном тепловом состоянии и температура Т в каждой его точке есть функция только одной координаты х, то согласно закону теплопроводности Фурье количество теплоты, испускаемое в секунду, описывается дифференцированным уравнением

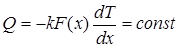, (1.48)

где 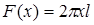— площадь теплообмена;

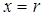— радиус трубопровода;

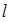— длина трубы.

Подставив F(x) в (1.48), получим , и, разделяя переменные, находим

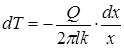. (1.49)

Интегрируя обе части (1.49) 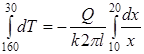или 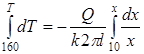, получаем систему уравнений

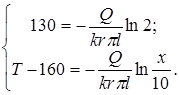(1.50)

Разделив почленно второе уравнение системы (1.50) на первое, получим 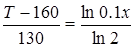, откуда, после некоторых преобразований находим закон распределения температуры в изоляции трубопровода (на рисунке кривая 160 ºC — 30 ºC)

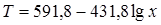. (1.51)

Преобразования: ;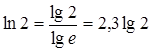

;

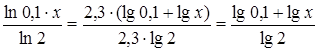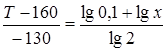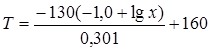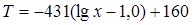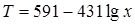(с округлениями).

⇐ Предыдущая 1 2 345 Следующая ⇒