ПЗ: Методология исследовательской деятельности в машиностроении

ПЗ: Методология исследовательской деятельности в машиностроении

Для гр. КТПм-19-о на 25.03.2020г.

(дистанционное обучение)

Задачипо разделу «Физическое моделирование» – по оценке величины. Задачи по разделу «Физическое моделирование» – по определению физических зависимостей.

1. МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ

Приведено решение задач с привлечением дифференциальных и интегральных уравнений, как наиболее универсальных методов. Применены однородные дифференциальные уравнения первого порядка, которые имеют наиболее широкую область применения.

В приведенных задачах использованы уравнения трех видов:

¾ дифференциальные уравнения в дифференциалах;

¾ дифференциальные уравнения в производных;

¾ простейшие интегральные уравнения с преобразованием в дифференциальные уравнения.

Основой решения задач по математическому моделированию является раздел 2, часть первая, данного учебного пособия и литературные источники [22, 24].

Задача 1.1

Источник света помещен в точке 0.

Найти форму зеркала, чтобы отраженные лучи были параллельны оси OХ.

С учетом физических законов изобразим на рисунке 1.1 схему формирования отраженного луча света.

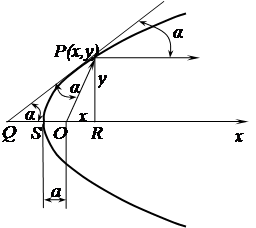
Рисунок 1.1 — Схема к решению задачи 1.1

Угол падения луча 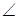OPQ равен углу отражения 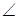OQP. Так как 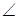OQP равен α, то треугольник OPQ — равнобедренный треугольник, а поэтому —│OQ│=│OP│= 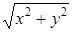. Считая, что y>0 можно записать, что

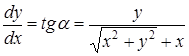Освобождаясь от иррациональности в знаменателе, умножим числитель и знаменатель дроби на 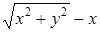, тогда получаем

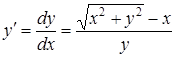. (1.1)

Из (1.1) имеем

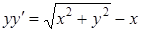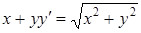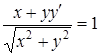; ; . (1.2)

Выражение (1.2) есть дифференциальное уравнение

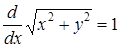. (1.3)

Об этом нужно догадаться. Проверим, что это так. В (1.3) разделим переменные 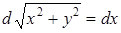и продифференцируем, в результате чего получим

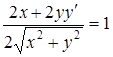или 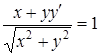. (1.4)

Как видим (1.3) и (1.4) совпадают. Значит, наша догадка правильна.

Проинтегрировав 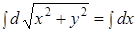, имеем

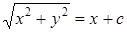. (1.5)

где с — постоянная интегрирования.

Возведя левую и правую части уравнения (1.5) в квадрат, получим

или

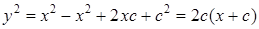. (1.6)

По условию задачи¸ кривая должна быть симметрична относительно оси OX, поэтому квадратное уравнение будет действительно при y<0. Значит уравнение (1.6) есть уравнение симметричной параболы с осью OX.

Расстояние от источника света О до центра зеркала S есть │OС│= a. Тогда начальное условие будет 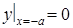. Подставляя 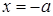в (1.6), получаем уравнение

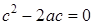. (1.7)

Имеем неполное квадратное уравнение (1.7). Решая его по формуле

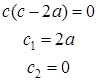Полученное значение 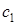подставляем в (1.6) и получаем уравнение параболы

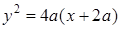или .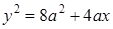

Для этой параболы положение точки P(x,y) на зеркальной поверхности относительно оси OX находится на расстоянии P=2a. Следовательно, фокусное расстояние P/2=a, и поэтому источник света должен находиться в точке О, т. е. в фокусе, чтобы обеспечить параллельную направленность лучей отраженных от зеркальной поверхности рефлектора.

12 3 4 5 Следующая ⇒