Хелпикс

Главная

Контакты

Случайная статья



Задача 1.6

⇐ ПредыдущаяСтр 3 из 5Следующая ⇒


Задача 1.6

Стальная шаровая оболочка с внутренним радиусом 6 см и внешним радиусом 10 см находится в стационарном тепловом состоянии. Температура на внутренней ее поверхности равна 200 ºС. Найти температуру на расстоянии r от центра и количество теплоты, которое в 1 с шар отдает наружу при теплопроводности k=0,14.

На основании симметрии шара можно считать, что теплота в шаре распространяется радиально. На расстоянии r от центра площадь передачи тепла равна площади поверхности сферы, т. е. .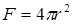

Поскольку между сферическими плоскостями количество тепла остается неизменным, так как через две любые поверхности протекает одно и тоже количество теплоты, то скорость, с которой теплота распределяется через площадь F описывается выражением законом Фурье (рисунок 1.3).

 

                                                 ,                                       (1.39)

 

где T — температура тела;

 k — коэффициент теплопроводности.

С учетом выражения для F уравнение (1.39) принимает вид

 

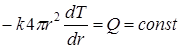                                         .                               (1.40)

 

Разделяя переменные (1.40), имеем

 

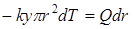                                             .                                    (1.41)

 

Интегрируя (1.41) 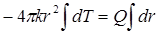, получим

 

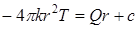                                или 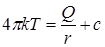                      (1.42)

 

(знак «–» опущен, так как он показывает потерю тепла).

 

 

Рисунок 1.3 — Схема теплопроводности в сферической оболочке к решению задачи 1.6

Для отыскания частного решения уравнения (1.42) подставим в него начальные условия: , 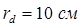; 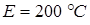,  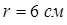и получим систему алгебраических уравнений

 

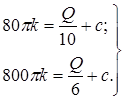                                                                                  (1.43)

 

Решим данную систему уравнений и найдем с и Q. Из 1-го уравнения системы находим постоянную интегрирования (1.43)

 

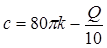                                                .                                       (1.44)

 

Подставив (1.44) во 2-ое уравнение системы (1.43), получим:

 

                                         ;

                                         ;

                                             ;

                                                ;

 

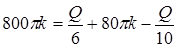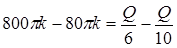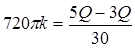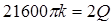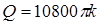                                                 .                                       (1.45)

 

Подставив (1.45) в 1-е уравнение (1.43), получим:

 

                                           ;

                                   ;

 

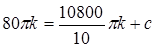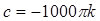                                                 .                                       (1.46)

 

Подставляя (1.45) и (1.46) в (1.42), находим решение задачи

 

                                       ,

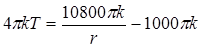отсюда

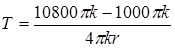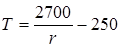                            ; ;                   (1.47)

 

                               .

 


⇐ Предыдущая12345Следующая ⇒
  

© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.