
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Сочетания
Сочетания
Сочетанием из 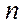 элементов по
элементов по 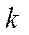 называется любое множество, составленное из
называется любое множество, составленное из  элементов, выбранных из данных
элементов, выбранных из данных 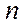 элементов.
элементов.
В отличие от размещений, сочетания различаются только элементами, и не имеет значения, в каком порядке заданы элементы.
Например, 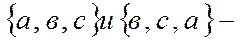 одно и то же сочетание.
одно и то же сочетание.
Число сочетаний из 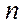 элементов по
элементов по 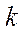 обозначается
обозначается 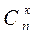 .
.
Число сочетаний, составленных из 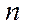 элементов по
элементов по 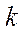 , вычисляется по формуле
, вычисляется по формуле 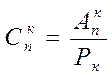 , т.е.
, т.е. 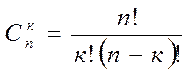
Задача 10.В вазе стоят 10 красных и 5 белых роз.
А)Сколькими способами можно составить букет из 3 роз?
Б) Сколькими способами можно составить букет из 1 красной и 2 белых роз?
Решение.
А) Так как порядок выбора роз не имеет значения, то выбрать 3 розы из15 можно 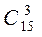 способами:
способами: 
Б). Одну красную розу можно выбрать 10 способами, а 2 белые из имеющихся 5 можно выбрать 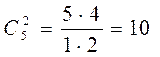 способами. Поэтому букет из 1 красной и 2 белых роз можно составить по правилу умножения,
способами. Поэтому букет из 1 красной и 2 белых роз можно составить по правилу умножения, 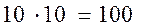 способами
способами
Задача 11. Из 9мальчиков и 11 девочек спортивного класса для участия в соревнованиях надо составить команду, в которую должны входить 3 мальчика и 3 девочки. Сколькитми способами это можно сделать?

Задача 12.На витрине магазина выставлено 6 сортов сыра и 5 видов йогурта. Покупателю требуется 2 куска сыра разных сортов и 3 йогурта разного вида. Сколькими способами покупатель может составить свою покупку?
Решение. Выбрать 2 сорта сыра из 6 имеющихся можно 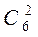 способами. Выбрать3 йогурта из 5 предлагаемых видов можно
способами. Выбрать3 йогурта из 5 предлагаемых видов можно  способами. По правилу умножения имеем
способами. По правилу умножения имеем 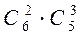 вариантов составления покупки.
вариантов составления покупки.
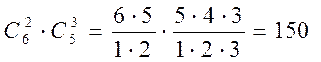 .
.
Задача 13.Сколько существует четырёхзначных чисел, у которых каждая следующая цифра меньше предыдущей?
Решение. Из 10 цифр (0;1;2;3;4;5;6;7;8;9) можно выбрать 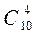 подмножеств, состоящих из 4 цифр. Расположив в каждой выбранной группе цифры в порядке убывания, получаем искомые четырёхзначные числа. При этом цифра 0 всегда будет стоять лишь последней, так как является наименьшей среди цифр.
подмножеств, состоящих из 4 цифр. Расположив в каждой выбранной группе цифры в порядке убывания, получаем искомые четырёхзначные числа. При этом цифра 0 всегда будет стоять лишь последней, так как является наименьшей среди цифр.

Задача 14. Сколько существует четырёхзначных чисел, у которых каждая следующая цифра больше предыдущей?
Решение. Искомые числа составляем из 9 цифр, исключив 0 (целое число не может начинаться с нуля). Количество искомых чисел равно 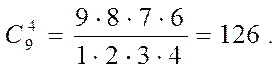
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|