Правило сложения.

Правило сложения.

Если элементов 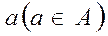может быть выбран m способами, а элемент может быть выбран n способами, то число способов, которыми можно выбрать один элемент из множества А или множества В, равно сумме m+ n.

Пример 4. В одной группе 25 студентов, в другой – 27 студентов. Сколькими способами можно выбрать одного ученика из двух групп?

Решение. 25+27=52

Правило умножения(основное правило комбинаторики).

Если элементов может быть выбран m способами, а элемент 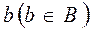после каждого выбора элемента а может быть выбран n способами, то число способов, которыми можно выбрать пару элементов и 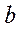в указанном порядке по одному из каждого множества, равно произведению .

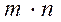Пример 5. В одной группе 25 студентов, в другой – 27 студентов. Сколькими способами можно выбрать двух студентов по одному из каждой группы?

Решение. Одного студента первой группы можно выбрать 25 способами, а из второй -27 способами. Двух студентов по одному из каждой группы (по правилу умножения) можно выбрать способами;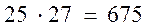

Пример 6. На книжной полке стоит 6 исторических романов и 4 приключенческих. Сколькими способами можно взять с полки 2 книги разных жанров?

Решение. По правилу умножения существует 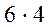способов взять с полки 2 книги разных жанров?

Пример 7. Собрание из 30 человек должно выбрать председателя и секретаря. Сколькими способами это можно сделать?

Решение. Председателем собрания можно выбрать 30 способами, после чего секретаря – 29 способами (из29 оставшихся членов собрания). По правилу умножения существует 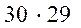способов выбора председателя и секретаря.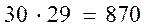

Пример 8. Сколькими способами можно рассадить 5 гостей за праздничным столом, если приготовлено 8 мест?

Решение. Для первого гостя имеется 8 возможностей выбрать место. После выбора места первым, для второго гостя остаётся 7 возможностей, аналогично для третьего гостя-6 возможностей (из 6 свободных мест), для четвёртого -5 вариантов, для пятого-4. По правилу умножения получаем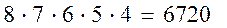

Пример 9. Из 10 членов шахматного кружка требуется составить команду из 3 человек для участия в соревнованиях. Сколькими способами это можно сделать?

Решение. Первого члена команды (на первую доску) можно выбрать 10 способами, после чего второго (на вторую доску0 – 9 способами, а третьего (на третью доску)- 8 способами.

Всего получаем вариантов выбора трёх шахматистов из десяти.

⇐ Предыдущая 123 4 5 Следующая ⇒