
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Перестановки
Перестановки
Перестановкой называется конечное множество, в котором установлен порядок его элементов.
Например, в множестве из одного элемента существует одна перестановка, в множестве из двух элементов – две.
Например, 
а;в;с а;с;в с;а;в с;в;а в;с;а в;а;с
Число перестановок из элементов обозначим через Рп.
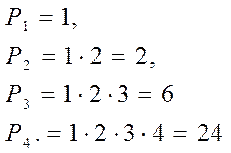
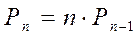
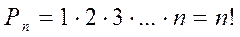
Для произведения первых 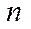 натуральных чисел принято специальное обозначение
натуральных чисел принято специальное обозначение 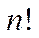 (эн - факториал)
(эн - факториал)
Например. 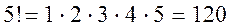
Число перестановок из п элементов равно произведению всех натуральных чисел от1 до п; 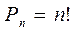
Задача 1. Если на завод приняли 6 токарей и их нужно закрепить за имеющимися 6 токарными станками, то возможностей будет 
У первого токаря имеется 6 возможностей выбрать станок,
у второго – уже только 5 возможностей,
у третьего – 4 возможности,
у четвёртого -3,
у пятого – две и, наконец,
у шестого – только одна возможность.
Задача 2. Сколькими способами семья из 5 человек может занять пять спальных мест в пятиместном гостиничном номере?
Решение. 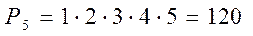
Задача 3. Каким числом способов 8 человек могут находится в очереди?
Решение. 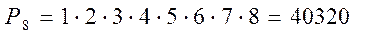
Задача 4. Сколько различных четырёхзначных чисел можно составить из цифр 9,7,5,0 если в каждом числе все цифры должны быть разными?
Решение. Если бы среди данных цифр не было нуля, то количество составленных из них четырёхзначных чисел (без повтора цифр в каждом числе) было бы равно количеству перестановок из4 элементов: 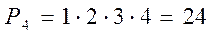 , но целое число не может начинаться цифрой 0. Среди найденных 24 чисел с цифрой 0 будет начинаться столько чисел, сколько существует перестановок из 3 элементов (цифр 9,7,5):
, но целое число не может начинаться цифрой 0. Среди найденных 24 чисел с цифрой 0 будет начинаться столько чисел, сколько существует перестановок из 3 элементов (цифр 9,7,5):  .
.
Значит, четырёхзначных чисел, составленных из данных цифр, будет 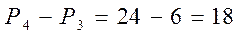
Задача 5. 9 студентов купили 9 билетов в театр. Сколькими способами они могут занять 9 кресел в театральном ряду, если Настя, Яна и Вика обязательно хотят сидеть рядом ( в любом порядке).
Решение. Будем считать трёх подруг (Настю, Яну и Вику) как один элемент общей компании, а три занятых ими кресла - как одно место. Тогда можем считать, что размещаем 7 человек в 7 креслах. Это можно сделать столькими способами, каково число перестановок из 7 элементов:  .
.
В то же время три подруги (Настя, Яна и Вика) в своих трёх креслах могут распределиться 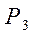 способами
способами  .
.
Таким образом, каждой перестановке из 7 элементов соответствует любая перестановка из трёх элементов. Всего перестановок по правилу умножения будет 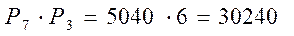
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|