
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Основные понятия комбинаторики
Основные понятия комбинаторики
Комбинаторика - раздел математики, в котором изучаются задачи выбора элементов из заданного множества и расположения их в группы по заданным правилам, в частности задачи о подсчете числа комбинаций (выборок), получаемых из элементов заданного конечного множества.
Множества и операции над ними.
Пересечением множеств 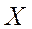 и
и 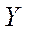 называется множество
называется множество 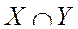 , состоящие из элементов, которые принадлежат как
, состоящие из элементов, которые принадлежат как 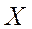 , так и
, так и 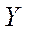 .
.
Пример 1. 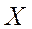 - множество чётных чисел меньших 10,
- множество чётных чисел меньших 10, 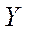 - множество делителей числа 24, тогда множество
- множество делителей числа 24, тогда множество 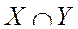 состоит из чисел принадлежащих и первому множеству и второму.
состоит из чисел принадлежащих и первому множеству и второму.
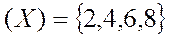
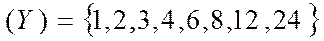
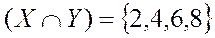
Пример 2. 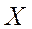 - множество прямоугольников,
- множество прямоугольников, 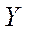 - множество ромбов, тогда множество
- множество ромбов, тогда множество 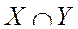 - квадратов.
- квадратов.
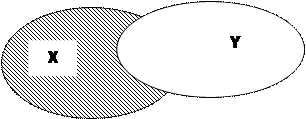
Объединением множеств 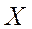 и
и 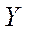 называется множество
называется множество 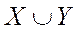 , состоящие из элементов, которые принадлежат хотя бы одному из множеств
, состоящие из элементов, которые принадлежат хотя бы одному из множеств 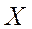 ,
, 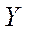 .
.
Пример 3.
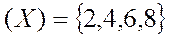
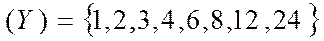
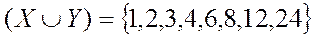
Пример 4. 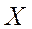 - множество прямоугольных треугольников,
- множество прямоугольных треугольников, 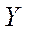 - множество равнобедренных треугольников, тогда множество
- множество равнобедренных треугольников, тогда множество 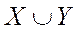 -……...
-……...
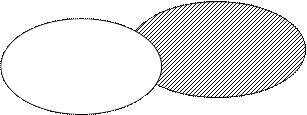
Разностью множеств 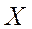 и
и 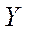 называется множество
называется множество 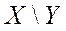 , состоящие из всех элементов множества
, состоящие из всех элементов множества 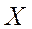 , не принадлежащих множеству
, не принадлежащих множеству 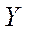 .
.
Пример 5.
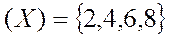
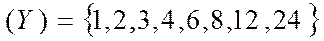
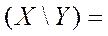 Ø
Ø
Диаграммы Эйлера – Венна
1. 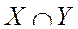
 |
2. 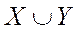
 |
3. 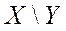
 |
 4.
4. 
| ||||
| ||||
Если каждый элемент множества 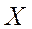 является в то же время элементом множества
является в то же время элементом множества 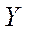 , то говорят, что
, то говорят, что 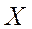 - часть, или, иначе, подмножество множества
- часть, или, иначе, подмножество множества 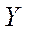 .
.
В этом случае пишут: 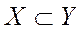
Например, множество квадратов является подмножеством ромбов, а множество ромбов - подмножеством множества параллелепипедов.
Множество натуральных чисел, делящихся на 10, является подмножеством множества чётных натуральных чисел.
Простейшие комбинаторные задачи можно решать методом перебора возможных вариантов.
Пример 1. Четыре студента группы изучают математику- Яна, Настя, Наташа, Андрей. На математическую олимпиаду требуется послать двух студентов. Сколькими способами это можно сделать?
| Яна | Настя | Наташа |
| Настя Наташа Андрей | Наташа Андрей | Андрей |
Пример 2. В меню столовой три первых блюда А1,А2,А3, два вторых В1,В2, и три сока С1,С2,С3. Сколько вариантов комплексного обеда можно составить из этих блюд?
Решение. Составляем схему возможных вариантов.
| А1 | А2 | А3 | |||
| В1 | В2 | В1 | В2 | В1 | В2 |
| С1,С2,С3 | С1,С2,С3 | С1,С2,С3 | С1,С2,С3 | С1,С2,С3 | С1,С2,С3 |
Если множество содержит конечное число элементов, и они расположены в установленном порядке, то такое множество называется упорядоченное множество.
Например, упорядоченное множество образуют 33 буквы русского алфавита; множество студентов группы, если за порядок принять список журнала,…
Пример 3. В посёлке имеется 5 светофоров. Каждый может находиться в одном из трёх состояний (гореть красным, зелёным или жёлтым светом). Сколькими способами можно зажечь все светофоры?
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|