
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Гомоморфизм и изоморфизм групп.
Примеры.
1) (Z, +) − циклическая группа с образующим элементом 1.
2) Группа корней n-ой степени из 1 − циклическая мультипликативная группа с образующим элементом, получаем по формуле (11) из § 1 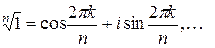 при
при 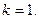
6°.Гомоморфизм и изоморфизм групп.
Определение 18. Пусть 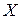 и
и 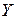 − множества,
− множества,  и
и  − бинарные операции (на
− бинарные операции (на 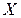 и
и 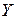 соответственно). Гомоморфизмом из
соответственно). Гомоморфизмом из 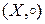 в
в 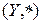 называется отображение
называется отображение 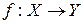 такое, что
такое, что 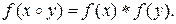
Пример. Отображение 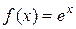 является гомоморфизмом из (R, +) в (R,
является гомоморфизмом из (R, +) в (R, 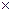 ). Это следует из справедливости равенства
). Это следует из справедливости равенства 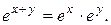
Замечания.
1. Аналогично определяется понятие гомоморфизма, если на множествах 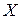 и
и 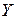 определены несколько операций.
определены несколько операций.
2. Так как полугруппа, группа, кольцо и так далее являются множествами с операциями, то очевидно, как определяются понятия гомоморфизма полугрупп, групп и так далее.
Определение 19.Изоморфизм − это биективный гомоморфизм.
Определение 20. Говорят, что пара 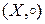 изоморфна паре
изоморфна паре 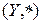 , если
, если 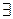 изоморфизм из
изоморфизм из 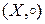 в
в 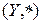 .
.
Обозначение. 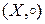
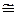
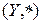 означает, что
означает, что 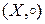 изоморфно
изоморфно 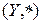 . Иногда пишут
. Иногда пишут 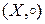
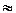
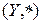 .
.
Примеры.
1) Отображение 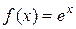 является изоморфизмом из (R; +) в (R>0;
является изоморфизмом из (R; +) в (R>0; 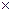 ). Действительно, это отображение является гомоморфизмом (см. предыдущий пример) и биективным отображением (в силу свойств экспоненциальной функции).
). Действительно, это отображение является гомоморфизмом (см. предыдущий пример) и биективным отображением (в силу свойств экспоненциальной функции).
2) В начале §1 комплексные числа определялись как пары действительных чисел. Множество пар вида 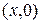 отождествлялись с множеством действительных чисел R. Это возможно в силу изоморфизма этих двух множеств.
отождествлялись с множеством действительных чисел R. Это возможно в силу изоморфизма этих двух множеств.
Отображение 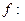 C
C 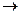 C такое, что
C такое, что 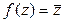 , является изоморфизмом.
, является изоморфизмом.
3) Отображение 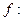 R
R 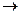 R такое, что
R такое, что 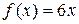 , является изоморфизмом аддитивной группы и не является гомоморфизмом мультипликативной группы. Действительно,
, является изоморфизмом аддитивной группы и не является гомоморфизмом мультипликативной группы. Действительно, 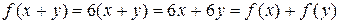 , но
, но 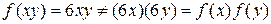 .
.
Теорема 7. Пусть 
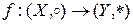 − изоморфизм. Тогда
− изоморфизм. Тогда
1) если 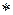 − коммутативна, то
− коммутативна, то 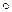 − также коммутативна;
− также коммутативна;
2) аналогично для ассоциативности;
3) если 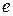 − нейтральный элемент в
− нейтральный элемент в 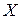 относительно
относительно 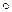 , то
, то 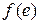 − нейтральный элемент в
− нейтральный элемент в 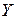 относительно
относительно 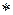 ;
;
4) если 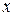 и
и 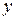 − взаимно обратные элементы из
− взаимно обратные элементы из 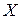 , то
, то 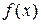 и
и 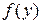 − взаимно обратные из
− взаимно обратные из 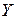 .
.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|