
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Свойства группы.. Кольцо, свойства кольца.. Примеры колец.
Свойства группы.
1) В группе G 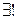 нейтральный элемент и
нейтральный элемент и 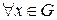
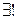 симметричный элемент.
симметричный элемент.
Доказательство следует из теорем 1 и 2.
2) Для  уравнения
уравнения 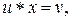
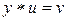 имеют единственное решение:
имеют единственное решение:
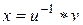 ,
, 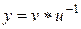 .
.
Доказательство. Покажем, что 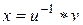 – решение уравнения
– решение уравнения 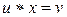 . Имеем:
. Имеем: 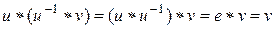 , то есть
, то есть 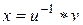 − решение.
− решение.
Если 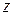 – другое решение, то
– другое решение, то 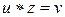
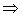 после умножения слева на
после умножения слева на 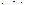
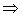
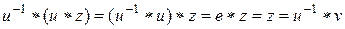
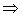

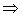
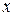 – единственное решение. Аналогично для другого уравнения.
– единственное решение. Аналогично для другого уравнения.
3) Закон сокращения в группе. Если 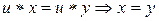 .
.
Доказательство следует из свойства 2).
3°. Кольцо, свойства кольца.
В алгебре изучаются множества и с несколькими, например, с двумя, алгебраическими операциями.
Определение 9. Непустое множество K называется кольцом и обозначается (K 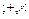 ), если выполняются условия:
), если выполняются условия:
1) (K, +) – абелева группа;
2) умножение ассоциативно, то есть 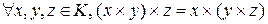 ;
;
3) умножение дистрибутивно относительно сложения, то есть
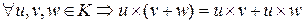 ,
, 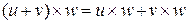 .
.
Кольцо называется коммутативным (понятия абелева кольца нет!), если умножение коммутативно. Если относительно умножения существует нейтральный элемент, то кольцо называется кольцом с единицей.
Примеры колец.
1. (Z; +, 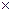 ), (Q; +,
), (Q; +, 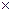 ), (R; +,
), (R; +, 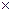 ) образуют коммутативные кольца с единицей относительно обычных операций сложения и умножения.
) образуют коммутативные кольца с единицей относительно обычных операций сложения и умножения.
2. Множество {0}, содержащее лишь одно число 0, образует кольцо, называемое нулевым кольцом.
3. Множество 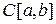 непрерывных на отрезке
непрерывных на отрезке 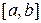 функций с операциями + и
функций с операциями + и 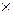 , определенными следующим образом:
, определенными следующим образом:
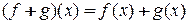 ,
, 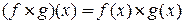 ,
,
образует коммутативное кольцо с единицей.
4. Множество V3 всех векторов пространства относительно операций сложения векторов и векторного произведения векторов не образует кольцо.
5. Рассмотрим пространство битовых строк (последовательностей длины 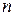 , состоящих из нулей и единиц), относительно операций
, состоящих из нулей и единиц), относительно операций 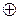 (исключающее «или») и
(исключающее «или») и 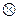 (логическое умножение), которые задаются таблицами:
(логическое умножение), которые задаются таблицами:
| ||
| ||
| 0 | ||
Например, (1010) 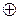 (0110)=(1100); (1010)
(0110)=(1100); (1010) 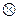 (0110)=(0010).
(0110)=(0010).
Операции 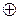 и
и 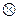 − алгебраические, нейтральный элемент – нулевая битовая строка (0…0). Для каждой битовой строки противоположным элементом является эта же битовая строка. Доказательство коммутативности, ассоциативности операций
− алгебраические, нейтральный элемент – нулевая битовая строка (0…0). Для каждой битовой строки противоположным элементом является эта же битовая строка. Доказательство коммутативности, ассоциативности операций 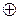 и
и 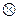 и дистрибутивность логического умножения
и дистрибутивность логического умножения 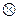 относительно операции
относительно операции 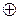 сводятся к доказательству этих свойств для битовых строк длиной 1, которое проводится прямыми вычислениями. Таким образом, пространство битовых строк с операциями
сводятся к доказательству этих свойств для битовых строк длиной 1, которое проводится прямыми вычислениями. Таким образом, пространство битовых строк с операциями 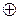 ,
, 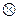 является кольцом, которое обозначается
является кольцом, которое обозначается 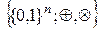 . Это кольцо является коммутативным кольцом с единицей.
. Это кольцо является коммутативным кольцом с единицей.
Так как ( 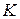 ;+) абелева группа, то
;+) абелева группа, то 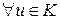
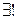 противоположный элемент
противоположный элемент 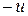 . Поэтому в К можно ввести операцию вычитания:
. Поэтому в К можно ввести операцию вычитания: 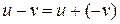 .В силу свойства группы
.В силу свойства группы 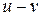 единственное решение уравнения
единственное решение уравнения 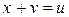 .
.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|