Хелпикс

Главная

Контакты

Случайная статья



Примеры.. Группа, свойства группы.

⇐ ПредыдущаяСтр 2 из 7Следующая ⇒


Примеры.

1. В (R, +) операция  сложения коммутативна и ассоциативна.

2. В (R, -) операция вычитания не коммутативна и не ассоциативна. Например, , .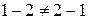

3. (R, 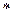), где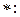 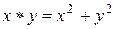, такая операция  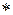коммутативна, но не ассоциативна. Действительно: .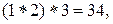

4. Умножение матриц является ассоциативной, но не коммутативной операцией.

Теорема 1(обобщённая ассоциативность). Если  операция ассоциативна, то в выражении 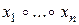 скобки можно расставлять в любых местах.

Доказательство. Проводится методом математической индукции. Для 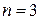 утверждение повторяет определение ассоциативности. Пусть 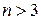. Рассмотрим выражения

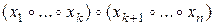и ,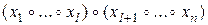

в которых выписаны лишь внешние скобки. Пусть 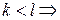 в силу предположения индукции эти выражения можно переписать в виде

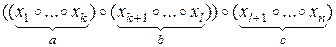
и

,

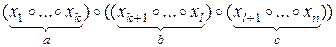ил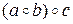и

 и

которые равны в силу определения ассоциативности. ■

Определение 4. Элемент  называется нейтральным относительно алгебраической операции , если

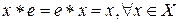. (1)

Теорема 2. Нейтральный элемент единственен.

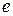Доказательство.  (от противного). Пусть  и ­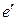− два нейтральных элемента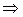

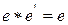(по условию нейтральност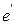и )    и

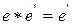 (по условию нейтральности )

.■

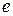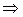
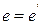Определение 5.Множество 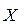с заданной на нем бинарной ассоциативной операцией называется полугруппой. Полугруппа с нейтральным элементом называется моноидом или полугруппой с единицей.

Определение 6. Элемент 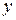 моноида  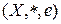называется симметричным к элементу 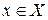, если

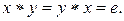
(2)

Теорема 3. Если в моноиде для 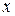есть симметричный элемент, то такой элемент единственен.

Доказательство. Пусть для данного 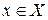 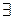два симметричных элемента  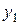и  Тогда в силу (1) и (2) имеем:       

                                .■

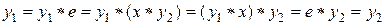Обычно умножение называют мультипликативной операцией, сложение – аддитивной. В случае мультипликативной операции результат операции 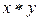называют произведением, нейтральный элемент – единицей (обозначают 1), симметричный элемент к  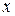– обратным (пишут 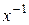). В случае аддитивной операции результат операции  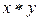называют суммой ( 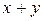), нейтральный – нулём (обозначают 0), симметричный – противоположным  (обозначают ).

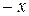Теорема 4. Если в моноиде 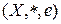для элементов  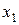и  есть симметричные элементы 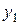 и  соответственно, то для элемента 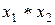также существует симметричный элемент, равный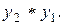

Доказательство.Для  доказательства теоремы необходимо проверить условия (2):  Проверим первое из этих равенств. Имеем:

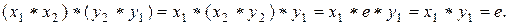
Аналогично проверяется второе условие из (2).■                             

2°. Группа, свойства группы.

Определение 7.Непустое множество G с заданной алгебраической операцией 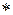 называется группой, если

1) 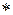 – ассоциативная операция;

2) в G 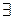 нейтральный элемент ;

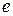3)  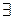симметричный элемент из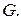

Если 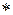 – коммутативная операция, то группа называется коммутативной или абелевой.

Операция, относительно которой G − группа, называется групповой операцией. Если групповая операция 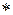 − умножение, то группа называется мультипликативной, если  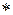– сложение, то G – аддитивная группа.

Примеры.

1. (N,+) ­– коммутативная полугруппа без нейтрального элемента.

2. (N, ) ­– коммутативная полугруппа с нейтральным элементом.

3. (Z, +) –  аддитивная абелева группа.

4. (Q, +) –  аддитивная абелева группа.

5. (R, +) –  аддитивная абелева группа.

6. (R, 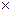) –  абелева полугруппа с нейтральным элементом.

7. (R ) –  мультипликативная абелева группа.

8. – абелева группа: .

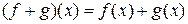9. Множество векторов на плоскости или в пространстве относительно операции сложения образуют абелеву группу.


⇐ Предыдущая1234567Следующая ⇒
  

© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.