Хелпикс

Главная

Контакты

Случайная статья



Теорема об обратной функции.. Теорема о непрерывности элементарных функций.. Тригонометрические функции и обратные к ним. Графики.. Теорема Вейерштрасса (без доказательства).. Определение равномерной непрерывности.. Теорема Кантора.. Примеры равномерно не

⇐ ПредыдущаяСтр 4 из 5Следующая ⇒


33. Теорема об обратной функции.

Теорема:

Пусть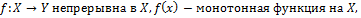

Доказательство:

.

 

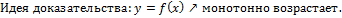
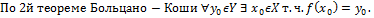
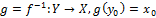34. Теорема о непрерывности элементарных функций.

Теорема:

Элементарные функции непрерывны в своей области определения.

 

35. Тригонометрические функции и обратные к ним. Графики.

1)

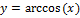
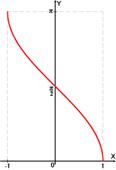
2)

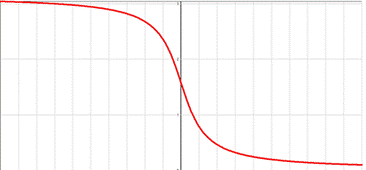
3)

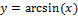
4)

 

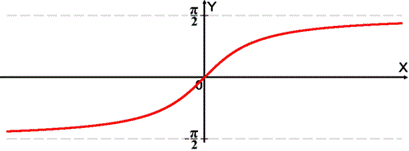
36. Теорема Вейерштрасса (без доказательства).

Теорема:

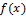 непрерывна на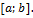

Если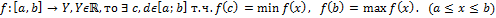

 

37. Определение равномерной непрерывности.

 

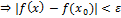
38. Теорема Кантора.

Теорема:

 

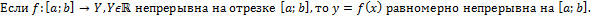
39. Примеры равномерно непрерывных функций.

1)

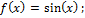
2)

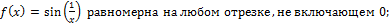
3)  

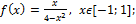
4)

 

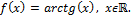
40. Задача о скорости движущейся точки.

Рассмотрим свободное падение материальной точки.






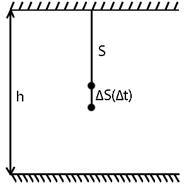
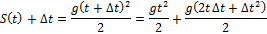
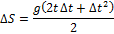
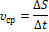
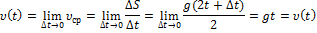
41. Определение производной.

Пусть . Если существует конечный 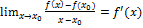, то он называется производной функции  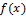в точке .

 

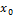42. Вывод табличных производных.

 

43. Теорема о производной обратной функции.

Теорема:

Пусть .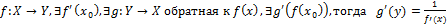

Доказательство:

 

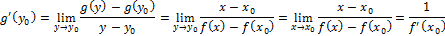
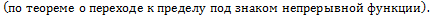
44. Геометрический смысл производной.

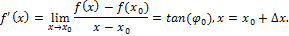
Рассмотрим график функции 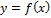. Точки M и N имеют следующие координаты M 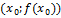, N 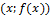. Угол между секущей MN и осью  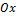обозначим .

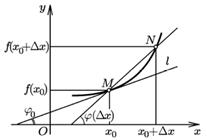
Если 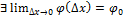, то  наклона касательной, проходящей через точку M 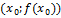, к положительному направлению оси  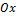является производной функции  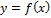в точке .

 

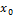45. Доказать, что функция 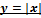 не имеет производной в нуле. Привести другой пример непрерывной функции, не имеющей производной в некоторой точке.

В нуле функция имеет излом (угол). Производные слева и справа не равны друг другу.

 


⇐ Предыдущая12345Следующая ⇒
  

© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.