
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Неопределенности. Примеры.. Монотонно возрастающие и монотонно убывающие последовательности.. Теорема о монотонно возрастающей ограниченной последовательности.. Предел функции (по Коши).. Предел функции (по Гейне).
10. Неопределенности. Примеры.
1)  Пример:
Пример: 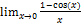
2)  Пример:
Пример: 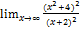
3) 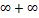 Пример:
Пример: 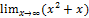
4) 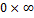 Пример:
Пример: 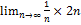
5) 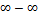 Пример:
Пример: 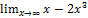
11. Монотонно возрастающие и монотонно убывающие последовательности.
Последовательность 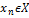 называется:
называется:
1) Неубывающей 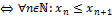
2) Невозрастающей 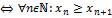
3) Возрастающей 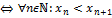
4) Убывающей 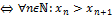
12. Теорема о монотонно возрастающей ограниченной последовательности.
Определение:
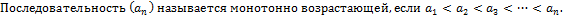 Определение:
Определение:
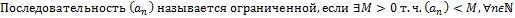 Теорема:
Теорема:
Монотонная ограниченная последовательность сходится.
Доказательство для монотонно возрастающей ограниченной последовательности:
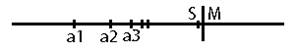
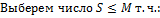
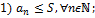
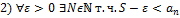
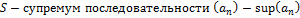
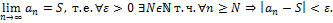
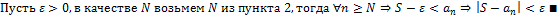
13. Число e.
Замечание:
Бином Ньютона:
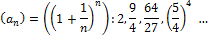
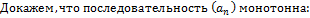
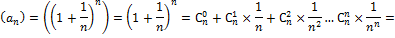
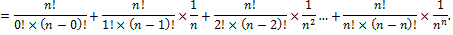
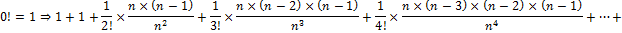
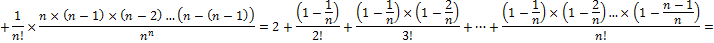
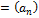
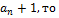
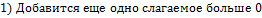
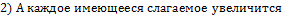
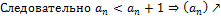
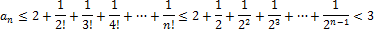
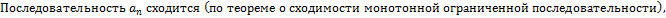
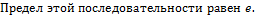
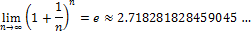
14. Предел функции (по Коши).
Число А называется пределом функции 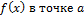 , если эта функция определена в некоторой окрестности точки
, если эта функция определена в некоторой окрестности точки 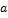 , за исключением, быть может, самой точки
, за исключением, быть может, самой точки 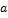 , и
, и 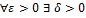 т.ч.
т.ч. 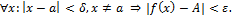
15. Предел функции (по Гейне).
Число А называется пределом функции 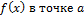 , если эта функция определена в некоторой окрестности точки
, если эта функция определена в некоторой окрестности точки 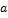 , за исключением, быть может, самой точки
, за исключением, быть может, самой точки 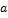 , и
, и 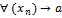 , соответствующая последовательность
, соответствующая последовательность 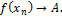
16. Доказать, что 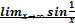 не существует.
не существует.
17. Односторонние пределы.
1) Число А называется пределом 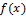 слева в точке
слева в точке 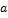 , если
, если 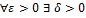 такое, что
такое, что 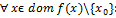
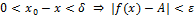 .
.
2) Число А называется пределом 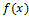 справа в точке
справа в точке 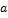 , если
, если 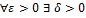 такое, что
такое, что 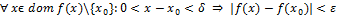 .
.
18. Свойства предела функции.
а) Если 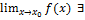 , то он единственный.
, то он единственный.
б) Если 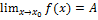 ,
, 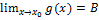 , то
, то
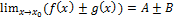
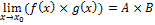
Если 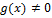 в окрестности
в окрестности 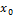 , а
, а 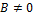 , то
, то 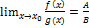
в) Если 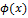 ограниченна в
ограниченна в 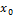 , а
, а 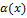 – бесконечно малая функция, то
– бесконечно малая функция, то 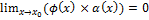
г) Первый замечательный предел 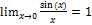
Доказательство:
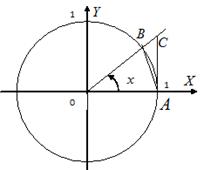
Рассмотрим площади трех фигур:
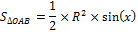
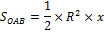
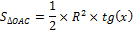
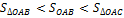
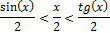
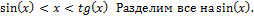
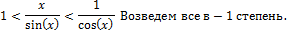

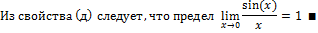
д) Пусть 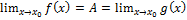
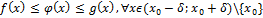
тогда 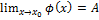
е) Второй замечательный предел 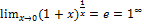
ж) Если 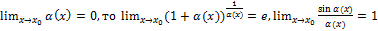
Если 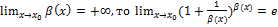
19. Доказать, что 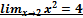 .
.
20. Вывести формулу для суммы геометрической прогрессии.
21. Критерий Коши для числовых последовательностей. Пример.
Теорема:
Предел числовой последовательности 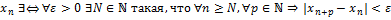
Доказательство:
Необходимость ( 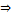 )
)
Пусть 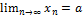 . Надо доказать, что
. Надо доказать, что 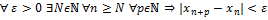
Пусть 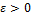
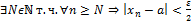
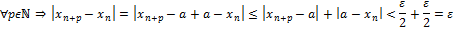
22. Критерий Коши для функций.
Предел функции 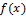 при
при 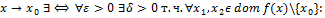
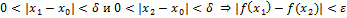
23. Определение бесконечно малой величины и понятие о – символики. Примеры.
Функция 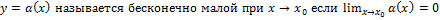
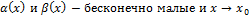
1) Если 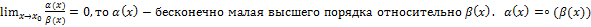 .
.
2) Если 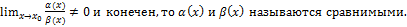
3) Если 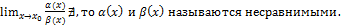
Пусть 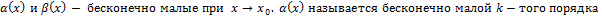
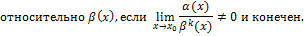
24. Теорема об эквивалентности бесконечно малых величин.
Определение:
Бесконечно малые величины 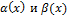 называются эквивалентными при
называются эквивалентными при 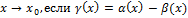 является бесконечно малой высшего порядка относительно
является бесконечно малой высшего порядка относительно 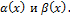
Теорема:
Пусть 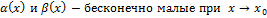 . Пусть
. Пусть 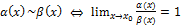 .
.
Доказательство:
Необходимость 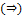 :
:
Пусть 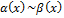 , т.е. по определению:
, т.е. по определению: 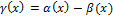 бесконечно малая высшего порядка, чем
бесконечно малая высшего порядка, чем 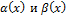 .
.
Тогда 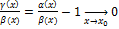 ,
,
т.к. 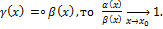
Достаточность 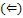 :
:
Пусть 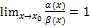 ,
,
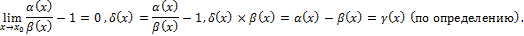
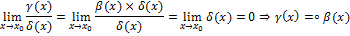
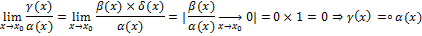
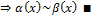
25. Определение непрерывной функции в точке и в области. Примеры.
1) Функция 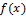 непрерывна в
непрерывна в 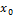
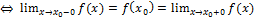 .
.
2) Функция 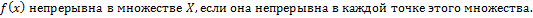
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|