
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Вопросы к экзамену по курсу «Математический анализ»
Вопросы к экзамену по курсу «Математический анализ»
(для студентов ФСУ группы: 422-1, 422-2, 422-3)
1. Понятие функции. Примеры.
Функцией 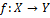 называется закон или правило, по которому каждому x из X ставится в соответствие единственное y из Y.
называется закон или правило, по которому каждому x из X ставится в соответствие единственное y из Y.
Примеры: 1)  ;
;
2) x+2y+1=0, y=-0.5*(x-1);
2. Композиция.
3. Определение предела числовой последовательности.
Функция 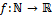 называется числовой последовательностью.
называется числовой последовательностью.
Число 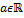 называется пределом числовой последовательности
называется пределом числовой последовательности 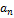 , если
, если 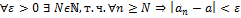 .
.
4. Доказать по определению, что 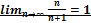 .
.
Пусть 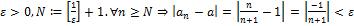
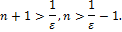
5. Дайте определение того, что 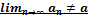 .
.
Если 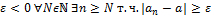
6. Теорема о единственности предела числовой последовательности.
Теорема:
Если предел числовой последовательности существует, то он единственный.
Доказательство:
Пусть 
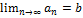 ,
, 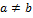
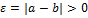 ,
, 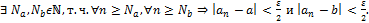
Тогда 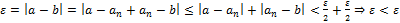
7. Теорема об арифметических свойствах предела числовой последовательности.
Пусть 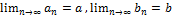 , тогда:
, тогда:
1) 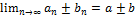
Доказательство:
Пусть 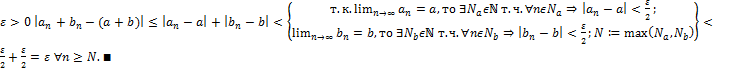
2) 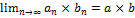
Доказательство:
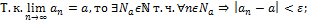
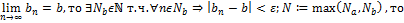

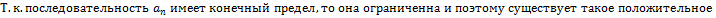
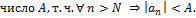
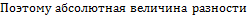

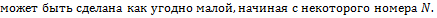
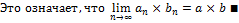
3) Если  ,
, 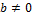 , то
, то 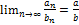
Доказательство:
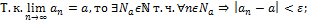

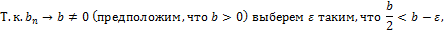
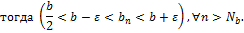
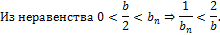

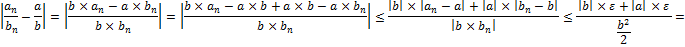
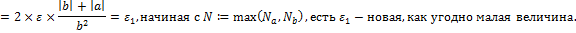
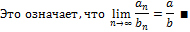
8. Определение:  ,
, 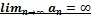 .
.
1) 
Определение: 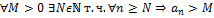
2) 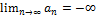
Определение: 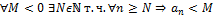
3) 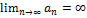
Определение: 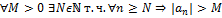
9. Бесконечно малые и бесконечно большие последовательности и их свойства. Примеры.
Бесконечно малая последовательность — это последовательность, предел которой равен нулю.
Бесконечно большая последовательность — это последовательность, предел которой равен бесконечности.
Свойства бесконечно малых последовательностей:
Ø Сумма двух бесконечно малых последовательностей сама также является бесконечно малой последовательностью.
Ø Разность двух бесконечно малых последовательностей сама также является бесконечно малой последовательностью.
Ø Алгебраическая сумма любого конечного числа бесконечно малых последовательностей сама также является бесконечно малой последовательностью.
Ø Произведение ограниченной последовательности на бесконечно малую последовательность есть бесконечно малая последовательность.
Ø Произведение любого конечного числа бесконечно малых последовательностей есть бесконечно малая последовательность.
Ø Любая бесконечно малая последовательность ограничена.
Ø Если стационарная последовательность является бесконечно малой, то все её элементы, начиная с некоторого, равны нулю.
Ø Если вся бесконечно малая последовательность состоит из одинаковых элементов, то эти элементы — нули.
Ø Если  — бесконечно большая последовательность, не содержащая нулевых членов, то существует последовательность
— бесконечно большая последовательность, не содержащая нулевых членов, то существует последовательность 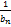 , которая является бесконечно малой. Если же
, которая является бесконечно малой. Если же  всё же содержит нулевые элементы, то последовательность
всё же содержит нулевые элементы, то последовательность 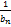 всё равно может быть определена, начиная с некоторого номера
всё равно может быть определена, начиная с некоторого номера 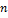 , и всё равно будет бесконечно малой.
, и всё равно будет бесконечно малой.
Доказательство: 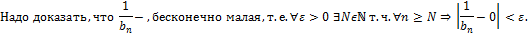
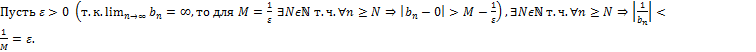
Ø Если  — бесконечно малая последовательность, не содержащая нулевых членов, то существует последовательность
— бесконечно малая последовательность, не содержащая нулевых членов, то существует последовательность  , которая является бесконечно большой. Если же всё же
, которая является бесконечно большой. Если же всё же  содержит нулевые элементы, то последовательность
содержит нулевые элементы, то последовательность  всё равно может быть определена, начиная с некоторого номера
всё равно может быть определена, начиная с некоторого номера 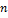 , и всё равно будет бесконечно большой.
, и всё равно будет бесконечно большой.
Доказательство:
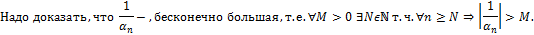
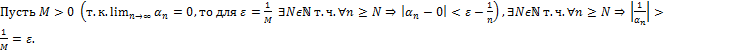
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|