
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Если в условии задачи требуется, чтобы два объекта были расположены рядом, необходимо
Если в условии задачи требуется, чтобы два объекта были расположены рядом, необходимо
2.9. Вычислите (в обычной тетради): а) 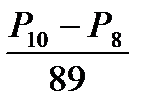 ; б)
; б)  ; в)
; в) 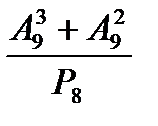 .
.
2. 3. СОЧЕТАНИЯ
Пример. В соревнованиях по футболу участвуют 4 команды: Шинник, ЦСКА, Динамо, Зенит. Сколько матчей будет сыграно, если турнир, организован по круговой системе (каждый участник встречается с каждым 1 раз)?
Решение:
Перебор возможных вариантов:
Перевод задачи на язык комбинаторики:
Исходное множество:
Выборки по
Порядок элементов в выборке:
Ответ: ________ матчей будет сыграно
Сочетанием из п элементов по т называют
Число сочетаний из п элементов по т находят по формуле:
Важно: элементы в каждом наборе (выборке) _______________________ повторяться
2.10. В бригаде из 10 человек троих нужно выделить для работы на новом участке. Сколькими способами это можно сделать?
Решение:
Исходное множество:
Выборки по
Порядок элементов в выборке:
Ответ:
2.11. На 6 сотрудников выделены 3 одинаковые путевки в санаторий. Сколькими способами их можно распределить?
Решение:
Исходное множество:
Выборки по
Порядок элементов в выборке:
Ответ:
2.12. На погранзаставе 40 рядовых и 15 офицеров. Сколькими способами из них можно составить наряд по охране границы, если он состоит из 2 офицеров и 4 рядовых?
Решение:
| Исходное множество: | ||
| Выборки по | ||
| Порядок элементов в выборке: |
Ответ:
2.13. Из 12 красных и 8 белых роз надо составить букет так, чтобы в нем были 3 красные и 2 белые розы. Сколькими способами это можно сделать?
Решение:
| Исходное множество: | ||
| Выборки по | ||
| Порядок элементов в выборке: |
Ответ:
2.14. В группе 15 студентов. Сколькими способами их можно разбить на 3 подгруппы численностью 3, 7 и 5 человек?
Решение:
| Исходное множество: | |||
| Выборки по | |||
| Порядок элементов в выборке: |
Ответ:
2.15.Вычислите: а) 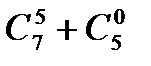 ; б)
; б) 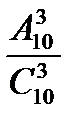 ; в)
; в) 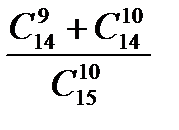 ; г)
; г) 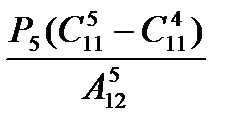 ; д)
; д) 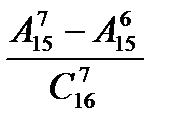 .
.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|