М2И ч.1 стр. 33,34

М2И ч.1 стр. 33,34

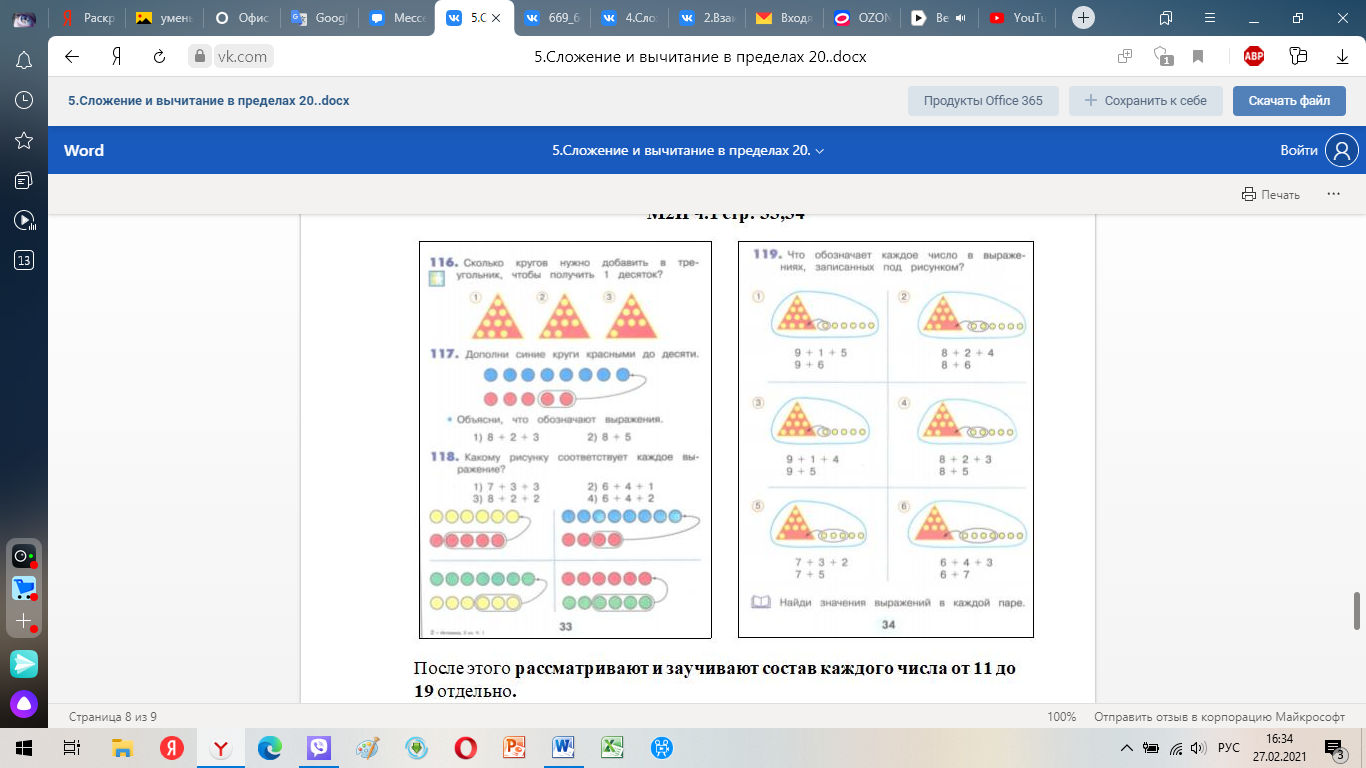
После этого рассматривают и заучивают состав каждого числа от 11 до 19 отдельно.

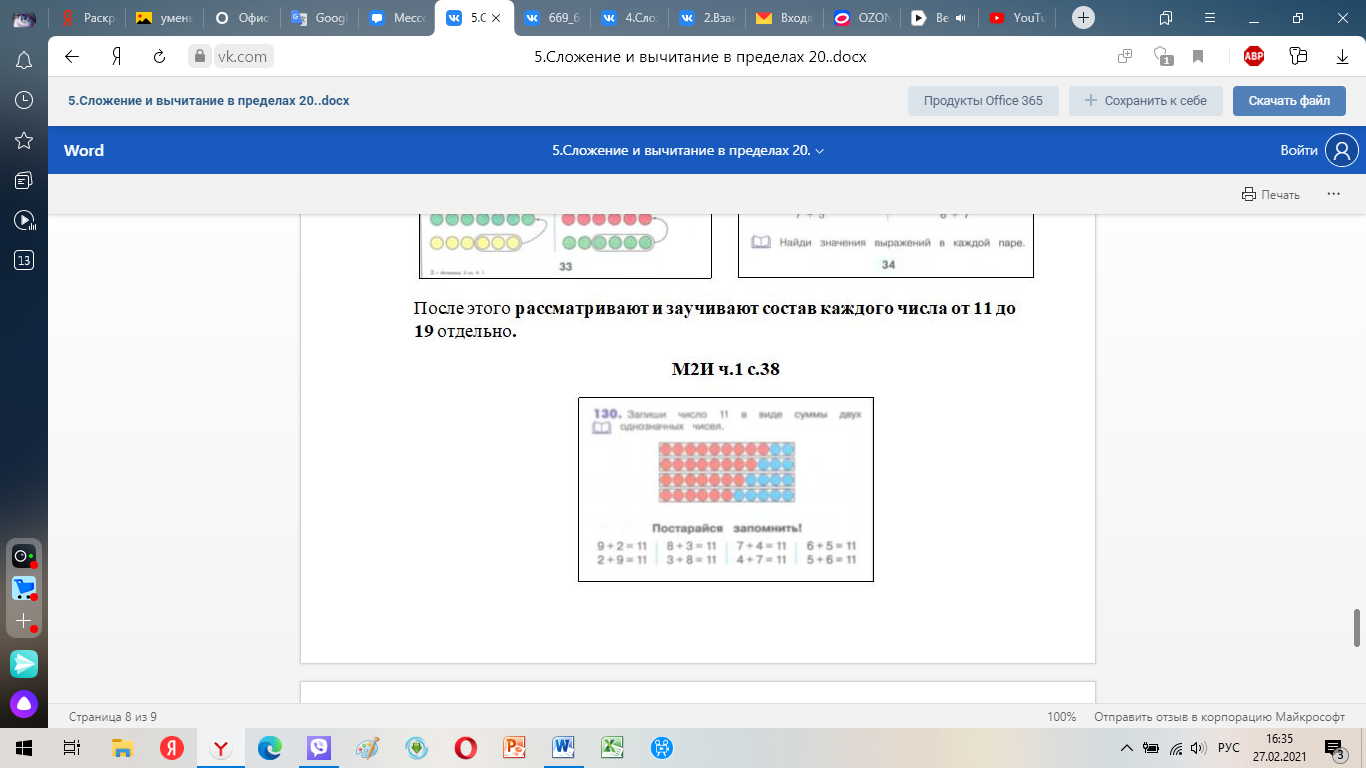
М2И ч.1 с.38

М2И ч.1 с.45

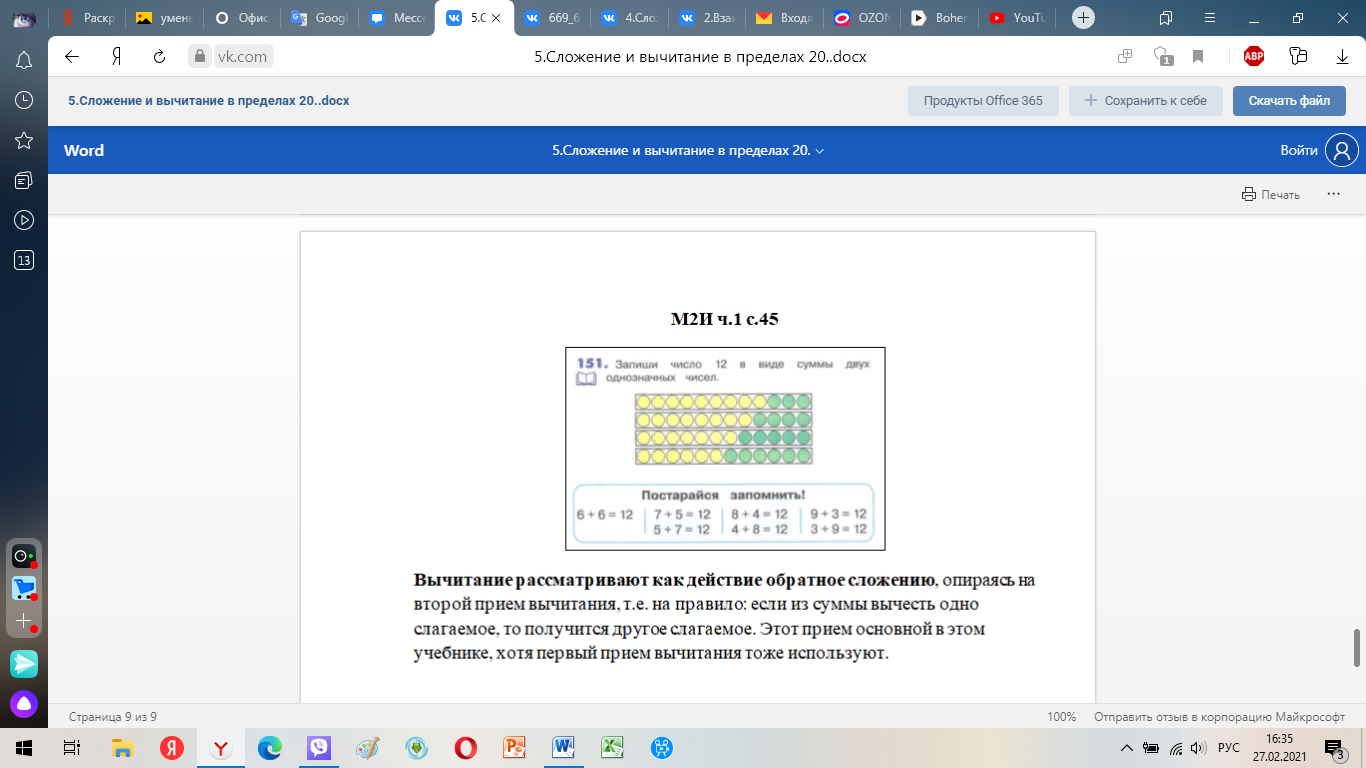
Вычитание рассматривают как действие обратное сложению, опираясь на второй прием вычитания, т.е. на правило: если из суммы вычесть одно слагаемое, то получится другое слагаемое. Этот прием основной в этом учебнике, хотя первый прием вычитания тоже используют.

16. Раскройте суть приема сложения однозначных чисел с переходом через десяток (7+5, 6+6 и т.д.). Какое наглядное пособие целесообразно использовать при знакомстве с вычислительным приемом сложения однозначных чисел вида (8+3, 7+5 и т.д.). Разработайте фрагмент урока, на котором дети знакомятся с этим приемом: М1М, ч. 2, стр. 64.

Данный прием заключается в решении примеров, где в ответе получается число больше 10.

Рассмотрим пример: 6+8

Обозначим числа цветными фигурами – кругами и квадратами (можно использовать наглядные пособия – кружки и квадраты).

Сколько будет кругов? (6). Выкладываем в ряд 6 кругов.

А сколько будет квадратов? (8). Выкладываем в ряд 8 квадратов.

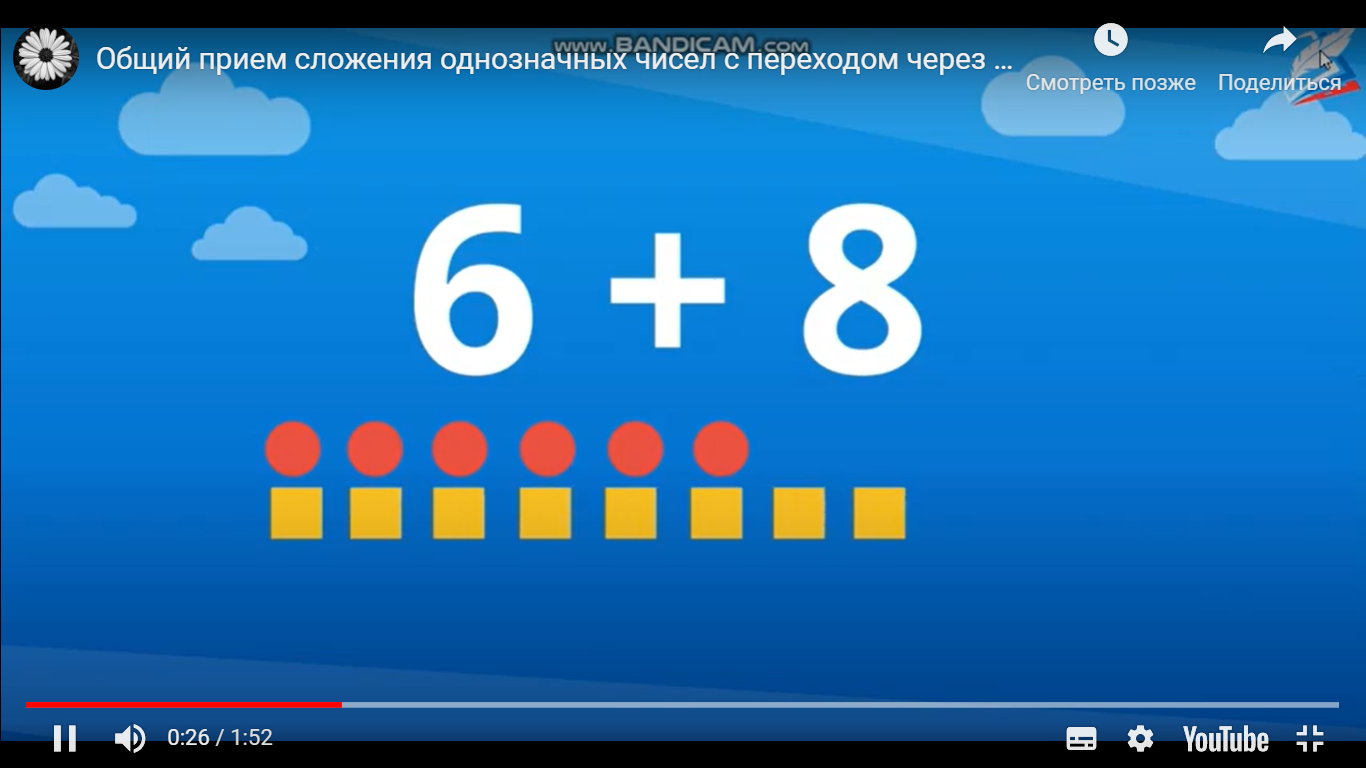
Как узнать, сколько всего фигур? (сложить все фигуры).

Какое число самое удобное для сложения? (число 10)

Сколько надо добавить фигур к 6, чтобы получить 10? (4). Переставляем фигуры таким образом:

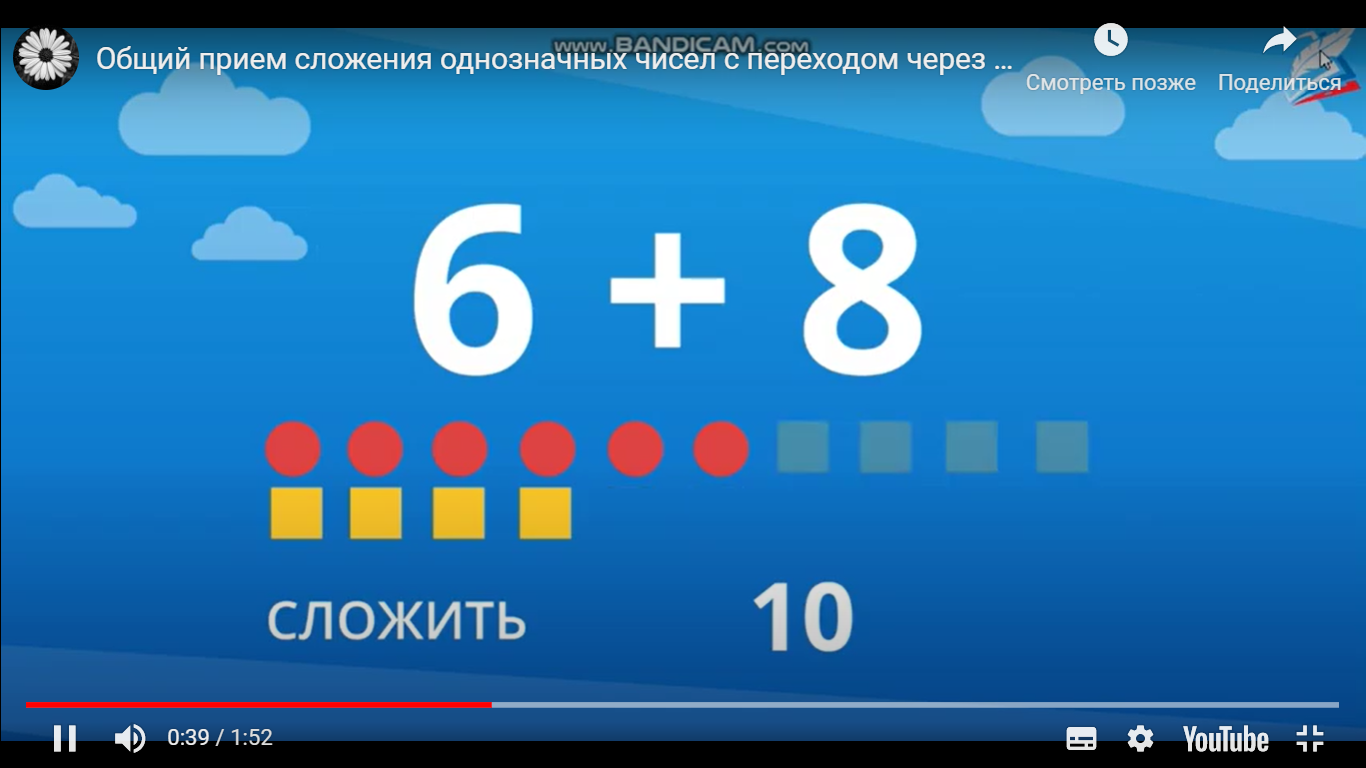
Сколько всего надо прибавить? (8). Снова переставляем фигуры.

Сколько уже прибавили? (4)

Сколько еще осталось прибавить? (4)

Сколько всего фигур получилось? (14)

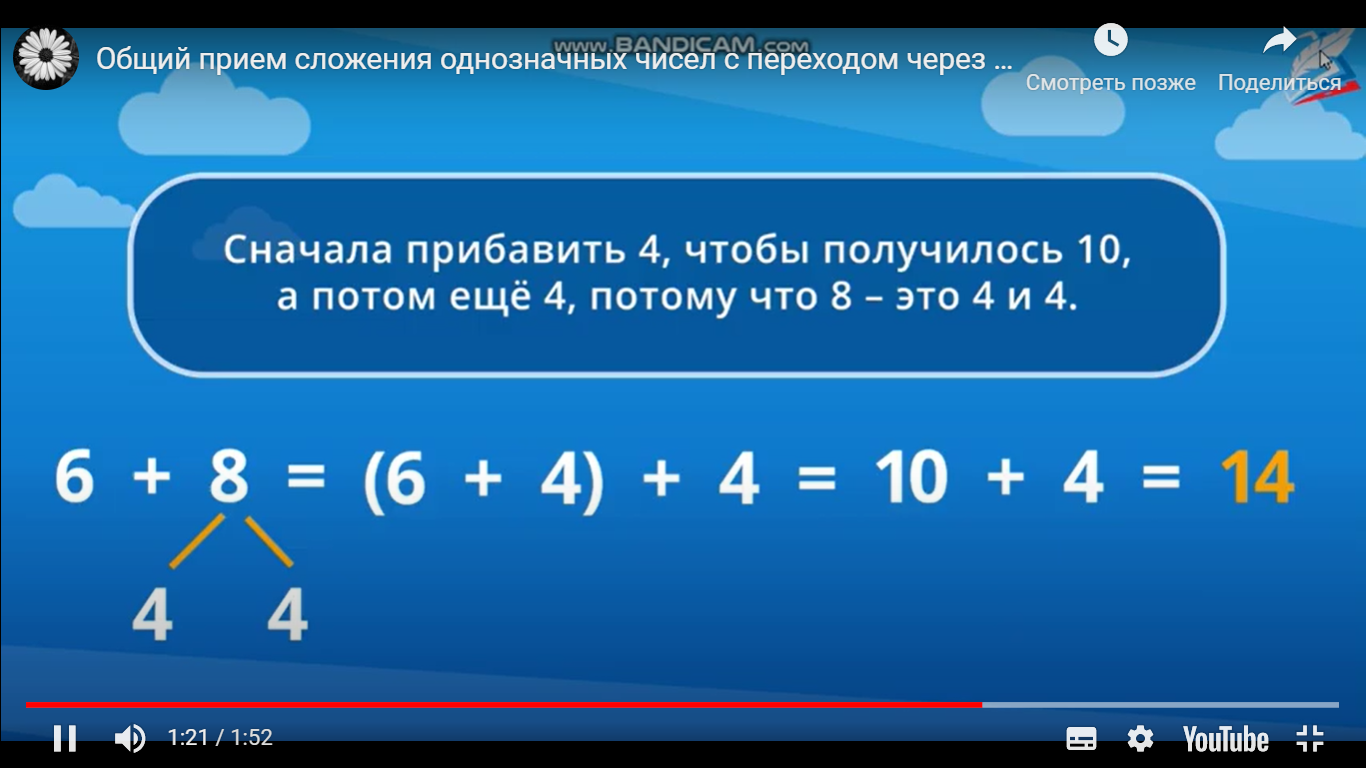
Как же к 6 прибавить 8?

Сначала к шести прибавить 4, чтобы получилось 10, а потом еще 4, потому что 8 – это 4 и 4.Значит, чтобы к 6 прибавить 8, надо число 8 разложить на удобные слагаемые так, чтобы было удобно добавить до 10, а потом прибавить то, что осталось.

При решении примеров на сложение с переходом через десяток нужен алгоритм действий:

1. Разложить слагаемое на удобные слагаемые так, чтобы добавить одно из слагаемых до 10.

2. Прибавить к 10 второе удобное слагаемое.

3. Вычислить результат.

⇐ Предыдущая 1 2 345 Следующая ⇒