г) интегральной теоремы Муавра-Лапласа.

+г) интегральной теоремы Муавра-Лапласа.

37.Формула Пуассона для вычисления вероятности того, что в n независимых испытаниях событие А произойдет m раз, имеет вид

a m e-a

а) P(m) ;

38.Если при вычислении вероятности того, что в серии из n независимых испытаний событие А произойдет m раз, известно, что вероятность p события А в каждом испытании мала, и число испытаний n велико, то лучше использовать формулу

а) Бернулли;

б) сложения вероятностей;

в) Пуассона;

+г) Муавра-Лапласа.

39.Монета брошена 2N раз (N велико). Вероятность того, что ―герб выпадет N раз, предпочтительнее вычислять по

+а) локальной теореме Муавра-Лапласа;

б) формуле Бернулли;

в) формуле Пуассона;

г) формуле сложения вероятностей.

40.Следующая функция называется функцией Лапласа

+а)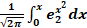

41.Вероятность выигрыша по одному лотерейному билету равна 1/7. Тогда вероятность того, что лицо, имеющее шесть билетов, не выиграет по двум билетам, равна

+г)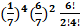

42.В партии очень большого объема имеется 95% небракованных изделий. В этом случае вероятность того, что среди взятых на испытание пяти изделий окажется более двух бракованных, равна

2! 3!

в) 1-((0,95)⁵+0,05·(0,95)⁴·5+

5! (0,05)2·(0,95)3);

43.В урне 20 белых и 10 черных шара, причем каждый вынутый шар возвращают в урну перед извлечением следующего. Вероятность того, что из четырех вынутых шаров окажется два белых, можно представить в виде

+a)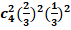

44.Десять осветительных лампочек елки включены последовательно. Вероятность перегореть для лампочки равна 0,1. Вероятность разрыва цепи равна

а)

10 0,1 10 ;

б) 1- C10

в) C0

+г) 1- C0

0,1 10 ;

0,9 10 ;

0,9 10 .

45. Вероятность того, что покупателю потребуется обувь 40-го размера, равна 0,4. Вошли трое покупателей. X — число покупателей, которым потребовалась обувь 40-го размера. Тогда P(X≥2) равна

а) 1– C0

0,4 0

0,6 3 ;

+б) C0

⇐ Предыдущая 1 2 3 4 567 Следующая ⇒