а) это число является наибольшим среди всех остальных;

⇐ ПредыдущаяСтр 5 из 7Следующая ⇒

+а) это число является наибольшим среди всех остальных;

б) оно совпадает с числом испытаний n;

в) оно соответствует наибольшей вероятности в данной серии испытаний;

г) событие, соответствующее этому числу, достоверно.

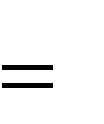
a m e-a

30.Формула Пуассона P(m)

а) при значениях p, близких к 1;

+б) при значениях p, близких к 0;

в) если p близко к 0,5;

г) при любом значении p.

, где a=np, дает наиболее точное значение вероятности

31.Наивероятнейшее число m₀ появления события в независимых испытаниях лежит в пределах

+в) np+p-1≤m0≤np+p;

32.Точную вероятность появления события m раз в серии из n испытаний дает формула

+а) Бернулли P_n(m)= C m

p m q n-m ;

33. Вероятность рождения мальчика равна 0,51. Тогда вероятность того, что среди 100 новорожденных окажется 50 мальчиков, вычисляется по формуле

+а) P=(1–0,51)50·0,51;

34. Монету бросают 5 раз. Вероятность того, что ―герб выпадет менее двух раз, равна (здесь P_n(m) — вероятность того, что в n испытаниях событие наступит m раз)

+г)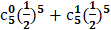

35.Локальная теорема Муавра-Лапласа вычисляет вероятность наступления события m раз в n испытаниях с большей точностью, если

а) n близка к нулю;

+б) 0≤n≤100;

в) mp+p-1≤n≤mp+p;

г) n достаточно велико.

36.Вероятность того, что в n независимых событие А наступит не менее m₁ и не более m₂ раз, можно вычислить

а) формулы полной вероятности;

б) теоремы произведения вероятностей;

в) потока событий;

⇐ Предыдущая 1 2 3 456 7 Следующая ⇒