г) формулу Байеса.. в) P(B/A)=∑P(Hi/A)P(B/HiA);. а) вероятность того или иного исхода каждого опыта не зависит от того, какие исходы имели другие опыты;

+б) 1/4;

в) 1/36;

г) 1/16.

23.Формула P(A)=P(H₁/A)+P(H₂/A)+…+P(H_n/A), где события H₁, H₂,…, H_n образуют полную группу событий, а событие А может произойти только с одним из них, представляет собой

а) формулу полной вероятности;

б) правило сложения вероятностей;

в) закон больших чисел;

+г) формулу Байеса.

24.Формула Байеса вычисления условной вероятности имеет вид

а) P(A/B)=P(A/B)/P(B)

б) P(Hi/A)=∑P(H_i)P(A/H_i);

+в) P(B/A)=∑P(Hi/A)P(B/HiA);

г) P(A/B)=P(A).

25. Имеются три одинаковых урны. В первой 2 белых и 3 черных шара, во второй — 4 белых и 1 черный шар, в третьей — 3 белых шара. Экспериментатор подходит к одной из урн и вынимает шар. Вероятность того, что это белых шар, равна

а)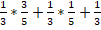

б)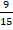

в)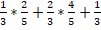

+г)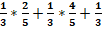

26.Опыты называются независимыми, если

+а) вероятность того или иного исхода каждого опыта не зависит от того, какие исходы имели другие опыты;

б) условия опыта не зависят от внешних факторов;

в) они проводятся в одинаковых условиях;

г) они имеют одинаковую вероятность.

27. В серии из n испытаний вероятность того, что событие А произойдет ровно m раз, если p — вероятность появления события А в одном испытании, можно вычислить по формуле

+а) (1–p)m-1·pn;)

28. Формула Бернулли для вычисления вероятности того, что событие А в серии из n испытаний появится m раз, имеет вид

+б) P_n(m)= C ^m p ^m q ^n-m ;

29.Число m₀ наступления события в серии из n испытаний называется наивероятнейшим числом, если

⇐ Предыдущая 1 2 345 6 7 Следующая ⇒