IV четверть (88 +2 часов)

IV четверть (88 +2 часов)

11.4A Исчисление II (20 часов)

Цели обучения

11.5.1.31 знать необходимые и достаточные условия вогнутости (выпуклости) графика функции на интервале; 11.5.1.32 определять интервалы выпуклости и вогнутости графика функции; 11.5.1.33 знать определение и уметь находить точки перегиба графика функции;

11.5.1.34 понимать связи между графиками функции и ее производных; 11.5.1.35 исследовать функцию с помощью производной и строить эскиз графика;

11.5.1.36 понимать связь между производными взаимно обратных функций; 11.5.1.37 находить производные обратных тригонометрических функций;

11.5.1.38 находить производную функции, заданной параметрически; 11.5.1.39 находить производную функции, заданной неявно;

11.5.1.40 находить производные n-го порядка;

11.5.1.41 знать и применять правило Лопиталя;

11.4B Вероятность и статистика (32 часа)

Тема урока

11.4.1.1 понимать целесообразность применения формул числа перестановок, сочетаний, размещений с повторениями; 11.4.1.2 выводить формулы для вычисления числа перестановок, сочетаний, размещений с повторениями; 11.4.1.3 решать комбинаторные задачи с использованием перестановок, сочетаний, размещений без повторений и с повторениями;

11.4.2.1 знать и применять правило умножения вероятностей; 11.4.2.2 знать формулу нахождения условной вероятности и применять её при решении задач;

11.4.2.3 знать формулу нахождения полной вероятности и применять её при решении задач; 11.4.2.4 знать условия использования формулы Байеса и уметь применять её при решении задач;

11.4.2.5 знать условия для реализации схемы Бернулли; 11.4.2.6 знать формулу Бернулли; 11.4.2.7 использовать формулу Бернулли при решении задач;

11.4.2.8 понимать, что такое дискретная случайная величина и знать её свойства; 11.4.2.9 создавать вероятностные модели реальных ситуаций и процессов; 11.4.2.10 знать понятия закона распределения и функции распределения дискретной случайной величины; 11.4.2.11 находить закон распределения дискретной случайной величины; 11.4.2.12 находить математическое ожидание, дисперсию и стандартное отклонение дискретной случайной величины; 11.4.2.13 применять свойства математического ожидания и дисперсии при вычислении;

11.4.3.1 определять, какая мера центральной тенденции (мода, медиана, среднее арифметическое) подходит для использования в заданной ситуации; 11.5.3.3 решать прикладные задачи с использованием мер центральной тенденции и мер рассеяния; 11.4.3.2 находить и интерпретировать значения показателей вариации (размах, межквартильный размах, дисперсия, стандартное отклонение); 11.4.3.3 определять, какой из показателей вариации подходит для использования в заданной ситуации;

11.4.3.4 строить и интерпретировать диаграмму «стебель-листья» из статистических данных; 11.4.3.5 строить и интерпретировать диаграмму «ящик с усами» из статистических данных, представленных в виде дискретных и интервальных вариационных рядов; 11.4.3.6 представлять и интерпретировать статистические данные в графическом виде, в том числе с помощью программного обеспечения;

11.4C Исчисление III (26 часов)

Цели обучения

11.5.1.42 выводить свойства первообразной, опираясь на правила дифференцирования; 11.5.1.43 находить неопределенный интеграл непосредственным интегрированием; 11.5.1.44 применять методы интегрирования по частям и подстановки для нахождения неопределенного интеграла; 11.5.1.45 интегрировать рациональные функции в том числе, с помощью разложения на простейшие дроби;

11.5.1.49 знать определение криволинейной трапеции; 11.5.1.46 знать определение определенного интеграла; 11.5.1.47 знать и применять формулу Ньютона-Лейбница; 11.5.1.48 применять методы интегрирования по частям и подстановки для нахождения определенного интеграла; 11.5.3.4 применять определенный интеграл для нахождения площади плоской фигуры;

11.5.3.5 знать и использовать формулу длины дуги кривой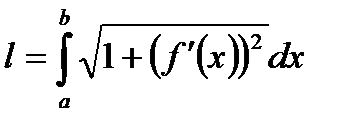

11.5.3.6 выводить и применять формулу для вычисления объема тела вращения с помощью определенного интеграла;

11.5.1.50 применять правило трапеции для приближенного вычисления определенного интеграла; 11.5.1.51 использовать эскиз, чтобы оценить, является ли приближенное значение интеграла, вычисленное с использованием правила трапеции, завышенным или заниженным;

11.5.1.52 иметь представление о несобственных интегралах; 11.5.1.53 вычислять несобственные интегралы в простых случаях;

11.5.1.31 - 11.5.1.41

11.4.1.1 – 11.4.1.3, 11.4.2.1 – 11.4.2.13, 11.4.3.1 – 11.4.3.6, 11.5.3.3

11.5.1.42 - 11.5.1.53, 11.5.3.4 – 11.5.3.6

⇐ Предыдущая 1 2 3 45