
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
III четверть (98+2 часа)
III четверть (98+2 часа)
11.3A Тригонометрия (30 часов)
| Цели обучения |
11.2.3.1 знать определения: αrcsinα, αrccosα, αrctgα  ;
11.2.3.2 выводить свойства αrcsinα, αrccosα, αrctgα ;
11.2.3.2 выводить свойства αrcsinα, αrccosα, αrctgα  ;
11.2.3.3 вычислять значения αrcsinα, αrccosα, αrctgα, ;
11.2.3.3 вычислять значения αrcsinα, αrccosα, αrctgα, 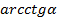 ;
11.2.3.4 знать и применять определения и свойства обратных тригонометрических функций;
11.2.3.5 строить графики обратных тригонометрических функций; ;
11.2.3.4 знать и применять определения и свойства обратных тригонометрических функций;
11.2.3.5 строить графики обратных тригонометрических функций;
|
| 11.2.3.6 решать простейшие уравнения и неравенства, содержащие обратные тригонометрические функции; |
| 11.2.3.7 обосновывать решения простейших тригонометрических уравнений; 11.2.3.8 решать тригонометрические уравнения (применением тригонометрических формул, сведением к квадратному уравнению, методами решения однородных уравнений первой или второй степени, разложением на множители, методом вспомогательного аргумента); 11.2.3.9 решать тригонометрические уравнения с помощью универсальной тригонометрической подстановки; 11.2.3.10 решать тригонометрические неравенства (применяя тригонометрические формулы, методом интервалов, методом замены переменной); 11.2.3.11 решать системы тригонометрических уравнений |
11.3B: Матрицы и определители (18 часов)
| Цели обучения |
| 11.2.4.1 знать виды матриц: квадратная, диагональная, единичная, нулевая; 11.2.4.2 выполнять действия над матрицами: сложение, умножение матрицы на число, умножение матриц, возведение в степень; |
| 11.2.4.3 знать понятие определителя матрицы и его свойства; 11.2.4.4 вычислять определители; 11.2.4.5 знать определение обратной матрицы и алгоритм вычисления обратной матрицы; 11.2.4.6 вычислять обратную матрицу, в том числе с помощью графического калькулятора; |
| 11.2.2.8 решать системы линейных уравнений методом Гаусса, методом Крамера, с помощью обратной матрицы; |
11.3C Векторы и координаты (40 часов)
| Цели обучения |
11.3.1.4 определять координаты точки и изображать точки в декартовой системе координат в пространстве;
11.3.3.4 решать простейшие задачи в координатах в пространстве: вычисление расстояния между двумя точками, определение середины отрезка, деление отрезка в данном отношении;
11.3.4.1 определять координаты вектора в пространстве;
11.5.2.2 понимать смысл терминов орт, радиус-вектор;
11.5.2.3 знать различные обозначения для векторов 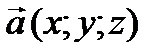 , , 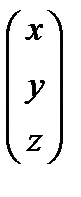 , а = xi+ yj + zk, , а = xi+ yj + zk, 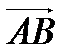 , a и другие;
11.3.4.2 вычислять длину вектора в пространстве; , a и другие;
11.3.4.2 вычислять длину вектора в пространстве;
|
| 11.3.4.3 выполнять действия над векторами в пространстве геометрически (сложение, вычитание, умножение вектора на число); 11.3.4.4 выполнять действия над векторами в пространстве в координатах; 11.3.4.5 знать и применять условие коллинеарности векторов в пространстве при решении задач; 11.3.4.6 знать определение компланарных векторов; 11.3.4.7 раскладывать вектор по трем некомпланарным векторам; |
| 11.3.4.8 знать определение и свойства скалярного произведения векторов в пространстве; 11.3.4.9 применять скалярное произведение векторов при решении задач; 11.3.4.10 знать определение и свойства векторного произведения векторов; 11.3.4.11 применять векторное произведение векторов при решении задач; 11.3.4.12 знать определение и свойства смешанного произведения векторов; 11.3.4.13 применять смешанное произведение векторов при решении задач; |
| 11.5.3.2 решать прикладные задачи, используя векторы; |
11.3.4.14 знать различные уравнения прямой и плоскости;
11.5.2.4 понимать значение всех символов, используемых в уравнениях прямой (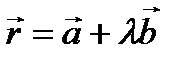 или или 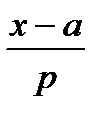 = = 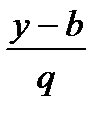 = = 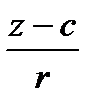 ) и плоскости (ax + by + cz + d = 0 или ) и плоскости (ax + by + cz + d = 0 или 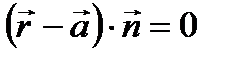 );
11.3.2.17 определять взаимное расположение двух прямых, прямой и плоскости, двух плоскостей, заданных уравнениями;
11.3.2.18 находить точку пересечения прямой и плоскости, заданных уравнениями;
11.3.3.5 находить расстояние между двумя прямыми, прямой и плоскостью, заданными уравнениями;
11.3.3.6 находить угол между прямой и плоскостью, угол между плоскостями, заданными уравнениями; );
11.3.2.17 определять взаимное расположение двух прямых, прямой и плоскости, двух плоскостей, заданных уравнениями;
11.3.2.18 находить точку пересечения прямой и плоскости, заданных уравнениями;
11.3.3.5 находить расстояние между двумя прямыми, прямой и плоскостью, заданными уравнениями;
11.3.3.6 находить угол между прямой и плоскостью, угол между плоскостями, заданными уравнениями;
|
| 11.3.4.15 выводить уравнение сферы; 11.3.4.16 составлять уравнение сферы; |
| 11.2.3.1 - 11.2.3.11 |
| 11.2.4.1 - 11.2.4.6, 11.2.2.8 |
| 11.3.1.4, 11.3.3.4-6, 11.5.2.2-3, 11.5.3.2 11.3.4.1 – 11.3.4.16 |
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|