гдеRa- сопротивление прибора; Rp - регулировочный резистор. 4 страница

В зависимости от объекта измерений, требуемой точности результата, диапазона рабочих частот и других условий для измерения параметров двухполюсников применяют различные методы и средства измерений. Наиболее распространёнными являются следующие методы измерения: вольтметра-амперметра, непосредственной оценки, мостовой, резонансный и дискретного счёта.

2.2.2. Метод вольтметра-амперметра

Измерение методом вольтметра-амперметра сводится к измерению тока и напряжения в цепи с измеряемым двухполюсником и последующему расчёту его параметров по закону Ома. Метод может быть использован для измерения активного и полного сопротивления, индуктивности и ёмкости.

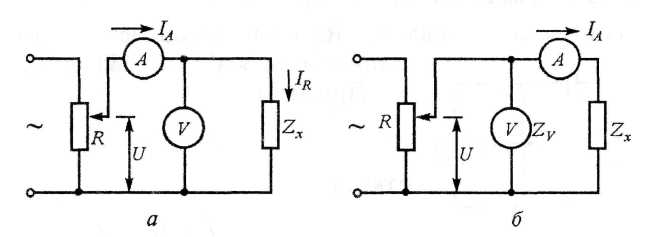
Измерение активных сопротивлений производится на постоянном токе, при этом включение резистора R_x в измерительную цепь возможно по схемам, представленным на рис. 2.1, а и б. Обе схемы включения приводят к методическим погрешностям DR, зависящим от величины

сопротивления приборов.

Рис. 2.1. Измерение активных сопротивлений методом вольтметра-амперметра

Очевидно, что в схеме на рис. 2.1, а методическая погрешность тем меньше, чем меньше сопротивление амперметра (при R_A= 0, DR = 0), а в схеме на рис. 2.1, б эта погрешность тем меньше, чем больше сопротивление вольтметра (при R_V= ¥ , DR = 0). Таким образом, схемой, приведённой на рис. 2.1, а, следует пользоваться для измерения больших сопротивлений, а схемой, приведённой на рис. 2.1, б - для измерения малых сопротивлений.

Измерение полного сопротивления Z_x выполняется на переменном токе частотой f (рис. 2.2). По показаниям вольтметра и амперметра определяют модуль полного сопротивления:

\Zx\ = U_v /1_A ,

где U_v, I_a - показания вольтметра и амперметра.

Выполнив анализ методической погрешности, придём к выводу, что схему, представленную на рис. 2.2, а, целесообразно применять при Z_x << Z_V , а на рис. 2.2, б - при Z_x >> Z_V .

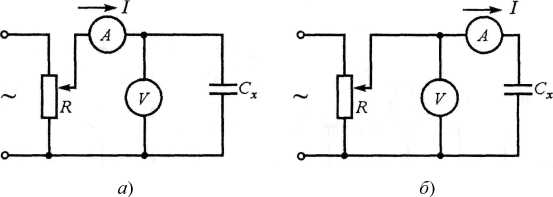
Измерение ёмкости методом вольтметра-амперметра может быть выполнено по схемам, представленным на рис. 2.3.

Емкостное сопротивление конденсатора

Х_с = 1/wC_x = U_c /I,

откуда

C_x = I/ wU_C,

где w= 2pf, f - частота тока в цепи; U_c - напряжение, измеряемое вольтметром.

Следовательно, при измерении ёмкости этим методом необходимо знать частоту источника питания f Для измерения больших ёмкостей рекомендуется схема, приведённая на рис. 2.3, а; а малых ёмкостей - на рис. 2.3, б.

Рис. 2.2. Измерение полного сопротивления двухполюсника

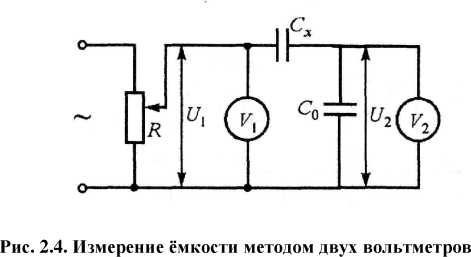
Для измерения очень малых ёмкостей применяют вариант метода вольтметра-амперметра (метод двух вольтметров), схема которого приведена на рис. 2.4.

Питающее напряжение U₁ измеряется вольтметром V_h Вольтметр V₂ измеряет напряжение на конденсаторе С₀, ёмкость которого известна:

U ₂ = I / wC₀.

Ток I определяется выражением

I = U₁ /(1/wC_x +1/wC₀),

откуда

Cx = CoU2/(U₁ -U₂).

Для уменьшения погрешности измерения необходимо выполнить условие С₀ >> С_х, тогда можно упростить выражение для С_х:

Cx = CoU 2/ Ui.

Метод двух вольтметров позволяет измерять ёмкости от долей пикофарад.

Рис. 2.3. Измерение ёмкости методом вольтметра-амперметра

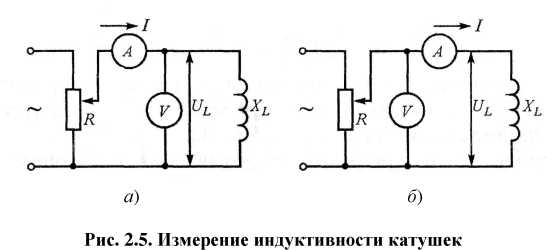
Измерение индуктивности катушки методом вольтметра- амперметра возможно, если её сопротивление R_L значительно меньше реактивного сопротивления X_L (рис. 2.5, а, б). При этом

I = U_L / wL,

откуда

L = U_L / wI.

Если требуется получить более точный результат, то

Необходимо учесть сопротивление катушки. Так как

L=1/w(V^кв⁽U_L/I)²-R²_L

Z =U_l/IV^квr²_L +w² L²,

Погрешности измерения параметров элементов цепей методом вольтметра-амперметра на низких частотах составляют 0,5 ... 10% и определяются погрешностью используемых приборов, а также наличием паразитных параметров. Погрешности измерения возрастают с увеличением частоты.

Метод непосредственной оценки. Метод непосредственной оценки реализуется в приборах для измерения сопротивления постоянному току - электромеханических и электронных омметрах. Электромеханические омметры строятся на основе приборов магнитоэлектрической системы и в зависимости от величины измеряемого сопротивления могут быть выполнены по схеме с последовательным (рис. 2.6, а) либо параллельным (рис. 2.6, б) включением измеряемого сопротивления.

Рис. 2.6. Электромеханический омметр

Источником питания омметра обычно служит гальванический элемент. Т ок, протекающий через магнитоэлектрический прибор в омметре с последовательным включением при разомкнутом ключе Кл, определяется по формуле

I =

U /^Rx+^RA+ ^R р,

гдеRa- сопротивление прибора; Rp - регулировочный резистор.

При постоянных значениях R_A, R_p и U отклонение стрелки прибора а определяется измеряемым сопротивлением R_x, т.е. шкала прибора может быть проградуирована в единицах сопротивления. Как следует из вышеприведённой формулы, шкала омметра неравномерна (рис. 2.6).

Перед проведением измерения сопротивления необходимо установить «размах» шкалы, т.е. отрегулировать омметр так, чтобы при R_x = ¥ и R_x = 0 стрелка прибора устанавливалась бы на начальную и конечную отметки шкалы. При незамкнутых входных зажимах омметра и разомкнутом ключе Кл (что соответствует R_x= ¥) стрелка прибора находится в крайнем левом положении. Следовательно, эта отметка шкалы будет соответствовать R_x = ¥. Далее, замкнув ключ Кл, т.е. моделируя R_x = 0, наблюдают отклонение стрелки прибора и в том случае, если стрелка не доходит до конечной отметки шкалы или переходит за нее, регулируют резистором R_p ток через прибор до достижения стрелкой конечной отметки. После этого, разомкнув ключ, можно выполнить измерение сопротивления R_x. Характер шкалы подсказывает, что омметр такого типа предпочтительно использовать для измерения сравнительно больших сопротивлений (до не

скольких килоом), так как при малых значениях R_x этот омметр имеет малую чувствительность.

Для измерения небольших сопротивлений применяются омметры, выполненные по схеме с параллельным включением измеряемого сопротивления, уравнение шкалы для которых имеет вид

I = U /[Rр + R_ARx /(R_A+ Rx)]. (2.1)

Как и в схеме с последовательным включением, здесь отклонение стрелки прибора зависит только от R_x при условии, что остальные члены уравнения (2.1) постоянны. Перед проведением измерения также необходимо установить размах шкалы, моделируя ситуацию R_x = 0 и R_р = ¥ и регулируя ток I сопротивлением резистора R_p. Для омметра с параллельным включением нулевое положение указателя совпадает с нулевым значением измеряемого сопротивления, а крайнее правое положение стрелки соответствует R_x = ¥. Шкала такого омметра изображена на рис. 2.6, б.

Омметры, выполненные по схемам на рис. 2.5, а, б, выпускаются как отдельные приборы, а также входят в состав комбинированных приборов (тестеров, авометров). Класс точности омметров не ниже 2,5.

Электронные омметры

При построении электронных омметров используются два метода измерения: метод стабилизированного тока в цепи делителя и метод преобразования измеряемого сопротивления в пропорциональное ему напряжение.

Схема измерения сопротивления по методу стабилизированного тока приведена на рис. 2.7, а.

Делитель напряжения, составленный из известного образцового R,_обр и измеряемого R_x сопротивлений, питается от источника опорного напряжения и_оп. Падение напряжения на образцовом резисторе усиливается усилителем У с большим входным сопротивлением. Выходное напряжение усилителя и_вых зависит от значения сопротивления R_x. В качестве индикатора обычно применяется микроамперметр магнитоэлектрической системы, шкала которого градуируется в единицах сопротивления. Если усилитель имеет коэффициент усиления K и входное сопротивление R^ >> R^, то измеряемое сопротивление определяется выражением

^Rx = (KUоп /Uвых -1)Rобр

Этот вариант схемы омметра применяется для измерения достаточно больших сопротивлений, когда R_x > Rобр.

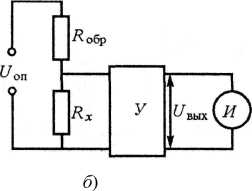
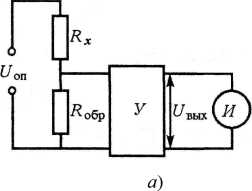
Рис. 2.7. Измерение сопротивления по методу стабилизированного тока

Для измерения малых сопротивлений (R_x < R_o6p) используется схема, представленная на рис. 2.7, б. Измеряемое сопротивление здесь определяется выражением

Rx =Rобр / (KUоп / U вых - 1).

Эта схема реализована в ряде выпускаемых промышленностью миллиомметров, обеспечивающих измерение активных сопротивлений в диапазоне 10^-4 ... 10² Ом с погрешностью 1,5 ... 2,0%.

Измерение средних и больших (до 10¹⁸ Ом) сопротивлений осуществляется с использованием преобразования измеряемого сопротивления в пропорциональное ему напряжение. В основу метода положен принцип работы операционного усилителя ОУ постоянного тока с отрицательной обратной связью (рис. 2.8).

Для схемы, представленной на рис. 2.8, а, измеряемое сопротивление R_x определяется выражением

R x=_ Rобр U оп/ Uвых,

где U_вых - выходное напряжение усилителя; Rобр- образцовый резистор

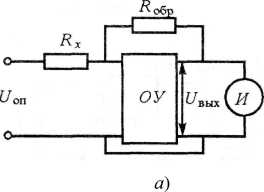
Рис. 2.8. Схемы омметров на основе операционных усилителей

(2.2)

При постоянных значениях U_on и Я_обр напряжение и_вых будет зависеть только от R_x и, следовательно, шкала микроамперметра может быть отградуирована в единицах сопротивления. Указанная схема применяется в основном для измерения больших сопротивлений в приборах, называемых тераомметрами.

Поменяв местами R_x и R^, получим схему (рис. 2.8, б), пригодную для измерения малых сопротивлений (от единиц ом). Измеряемое сопротивление в такой схеме определяется выражением

R x=_ Rобр U вых/ Uоп

Применение в одном приборе обоих вариантов схем позволяет создать измерители сопротивления с диапазоном измерения от единиц ом до нескольких десятков мегаом с погрешностью не более 10%.

ЛЕКЦИЯ №5

2.2.1. Измерительные мосты постоянного тока

Важным классом средств измерения, предназначенных для измерения параметров элементов электрических цепей методом сравнения, являются мосты. Сравнение измеряемой величины (сопротивления, ёмкости, индуктивности) с образцовой мерой при помощи моста в процессе измерения может осуществляться вручную или автоматически, на постоянном или на переменном токе. Мостовые схемы обладают большой точностью, высокой чувствительностью, широким диапазоном измеряемых значений параметров. На основе мостовых методов измерения строятся средства измерения, предназначенные как для измерения какой-либо одной величины, так и универсальные аналоговые и цифровые приборы.

Одинарный мост постоянного тока. Такой мост (рис. 2.9) содержит четыре резистора, соединённых в кольцевой замкнутый контур. Резисторы R₁, R₂, R₃ и R₄ этого контура называются плечами моста, а

Рис. 2.9. Схема одинарного моста постоянного тока

точки соединения соседних плеч - вершинами моста. Цепи, соединяющие противоположные вершины, называют диагоналями. Диагональ ab содержит источник питания и называется диагональю питания. Диагональ cd, в которую включен индикатор Г, называется измерительной диагональю. В мостах постоянного тока в качестве индикатора обычно используется гальванометр. Мосты постоянного тока предназначены для измерения активного сопротивления.

В общем случае зависимость протекающего через гальванометр тока I_г от сопротивлений плеч, сопротивления гальванометра R_T и напряжения питания U имеет вид

I _г =

U(R₁R₃-R₂R₄) (2.2)

[Rг(R₁+R₂)(R₃+R₄)+R₁R₂(R₃+R₄)+R₃R₄(R₁+R₂)]

Измерение сопротивления может производиться в одном из двух режимов работы моста: уравновешенном либо неуравновешенном. Мост называется уравновешенным, если разность потенциалов между вершинами с и d равна нулю, а, следовательно, и ток через гальванометр равен нулю.

Из (2.2) следует, что I_г = 0 при

(2.3)

R₁R₃ — R₂ R₄₌ 0.

Это условие равновесия одинарного моста постоянного тока (2.3) можно сформулировать следующим образом: для того, чтобы мост был уравновешен, произведения сопротивлений противолежащих плеч моста должны быть равны. Если сопротивление одного из плеч моста (например, R₄) неизвестно, то уравновесив мост путём подбора сопротивлений плеч R₁, R₂ и R₃_, находим из условия равновесия

R₄ =R₁R₃/R₂

В реальных мостах постоянного тока для уравновешивания моста регулируются отношение R₁/R₂ и сопротивление плеча R₃, которые, соответственно, называют плечами отношения и плечом сравнения.

В состоянии равновесия моста ток через гальванометр равен нулю и, следовательно, колебания напряжения питания и сопротивления гальванометра влияния на результат измерения не оказывают (важно лишь, чтобы чувствительность гальванометра была достаточной для надёжной фиксации состояния равновесия). Поэтому основная погрешность уравновешенного моста определяется чувствительностью гальванометра, чувствительностью схемы, погрешностью сопротивлений плеч, а также сопротивлениями монтажных проводов и контактов. При измерении малых сопротивлений существенным источником погрешности может явиться сопротивление проводов, с помощью которых измеряемый резистор подключается к входным зажимам моста, так как оно полностью входит в результат измерения. Поэтому нижний предел измерения одинарного моста постоянного тока ограничен значениями сопротивления порядка 1 Ом. Верхний же предел измерения 10⁶... 10⁸ Ом ограничивается чувствительностью гальванометра. При больших значениях измеряемого сопротивления токи в плечах моста очень малы и чувствительности гальванометра недостаточно для чёткой фиксации равновесия.

В режиме неуравновешенного моста измерение сопротивления производится по показаниям гальванометра, предварительно в комплекте с мостовой схемой отградуированного в единицах сопротивления. Неуравновешенные мосты часто применяются в устройствах для разбраковки изделий по сопротивлению (резисторов, обмоток реле и т.п.). Так, если при изготовлении резисторов необходимо отобрать из партии резисторы с сопротивлением R = ^_ном ± DR, то, уравновесив предварительно мост с помощью образцового магазина сопротивления при R_x = R^, изменяют сопротивление магазина на ± DR и фиксируют соответствующие отклонения стрелки гальванометра ±а (гальванометр с нулём посредине шкалы). Затем вместо магазина сопротивления к входу моста подключаются контролируемые резисторы, и если стрелка гальванометра выходит за допустимые пределы, резистор бракуется.

Неуравновешенные мосты по точности значительно уступают уравновешенным, так как на результат измерения кроме факторов, указанных для уравновешенных мостов, оказывают влияние колебания напряжения питания и сопротивления гальванометра.

2.2.1. Измерительные мосты переменного тока

Для измерения ёмкости, индуктивности, взаимной индуктивности и тангенса угла потерь конденсаторов применяются мосты переменного тока, схемы которых отличаются большим разнообразием. Кроме простых четырёхплечих мостовых схем существуют и более сложные мостовые схемы. Эти схемы путём последовательных эквивалентных преобразований могут быть приведены к простой четырёхплечей схеме, которая является, таким образом, основной.

Схемы одинарного четырёхплечего моста переменного тока приведены на рис. 2.10. Так как мост питается напряжением переменного тока, то в качестве индикатора в нём применяются электронные милливольтметры переменного тока либо осциллографические индикаторы нуля.

В общем случае сопротивления плеч моста переменного тока представляют собой комплексные сопротивления вида ^rZ_i = R_i + jX_i.

Аналогично соотношению (2.3) условие равновесия одинарного моста переменного тока имеет вид:

Z₁Z₃ = Z ₂Z₄.

Запишем это выражение в показательной форме:

Z_1e^jф1Z₂e^j^ф2=Z₃е^j^ф3Z₄e^j^ф4, (2.4)

где Z_h - модуль комплексного сопротивления; ф - фазовый сдвиг между током и напряжением в соответствующем плече.

Соотношение (2.4) распадается на два скалярных условия равновесия:

(2.5)

Z₁Z₃ = Z ₂ Z ₄; ф_l+ф₃=ф₂+ф₄.

Отсюда следует, что в схеме моста переменного тока равновесие наступает только при равенстве произведений модулей комплексных сопротивлений противолежащих плеч и равенстве сумм их фазовых сдвигов. При этом нужно иметь в виду, что при изменении значений активных и реактивных составляющих одновременно изменяются и модуль, и фаза, поэтому мост переменного тока можно привести к состоянию равновесия лишь большим или меньшим числом переходов от регулирования одного параметра к регулированию другого. Второе уравнение (2.5) показывает, какими должны быть сопротивления плеч мостовой схемы, чтобы обеспечить возможность её уравновешивания. Так, например, если в двух смежных плечах включены активные сопротивления ф = 0), то в двух других смежных плечах обязательно должны быть сопротивления одного характера - или индуктивности, или ёмкости.

Для измерения ёмкости конденсаторов без потерь используется мостовая схема, приведённая на рис. 2.10, а. Условие равновесия для этой схемы имеет вид

R₁ / wС_обр = ^R2 /^wCx,

где С_обр - образцовый конденсатор переменной ёмкости, откуда

Cx = (R₂/ R₁ )Собр.

Мостовая схема для измерения индуктивности приведена на рис. 2.10, б. В качестве плеча сравнения здесь также используется конденсатор переменной ёмкости С_обр. Полагая, что активное сопротивление катушки пренебрежимо мало (R_L = 0), получим условие равновесия

wLx / wС_обр = R₂R₄,

откуда

^Lx =R₂R₄C_обр.

Погрешность моста переменного тока определяется погрешностями значений элементов образующих мост, переходных сопротивлений контактов, чувствительностью схемы и индикатора. Мосты переменного тока больше, чем мосты постоянного тока, подвержены влия-

а) б)

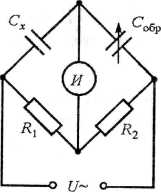
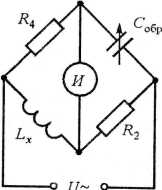
Рис. 2.10. Измерение сопротивления и ёмкости мостом переменного тока

нию помех и паразитных связей между плечами, плечами и землей, мостом и оператором. Именно поэтому, даже при тщательном экранировании моста и принятии других мер защиты, погрешности мостов переменного тока больше, чем погрешности мостов постоянного тока. Промышленностью выпускаются мосты переменного тока классов точности от 0,1 до 5,0.

Мосты переменного тока работают обычно на низких частотах 100 Гц и 1000 Гц. При работе на повышенных частотах погрешности измерения резко возрастают.

2.2.1. Резонансный метод измерения

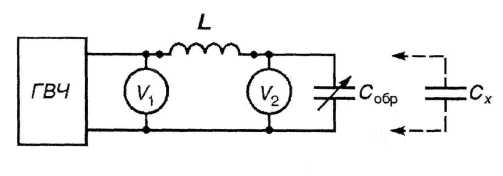
Резонансный метод измерения основывается на определении резонансной частоты колебательного контура, составленного из образцового и измеряемого элементов (индуктивностей или ёмкостей). Этот метод применяется для измерения индуктивностей и ёмкостей только на высокой частоте, так как в области низких частот резонансные явления проявляются недостаточно резко, что не позволяет получить высокую точность измерения. Известно несколько вариантов резонансного метода, на основе которых построены средства измерения параметров двухполюсников. Рассмотрим принцип действия прибора, называемого измерителем добротности или куметром. Схема измерителя добротности (см. рис. 2.11) включает источник питания - высокочастотный генератор (ГВЧ), последовательный колебательный контур, образуемый катушкой L с активным сопротивлением R_L и конденсатором С_обр. Напряжение на выходе генератора и на конденсаторе С_обризмеряется вольтметрами с высокоомным входом V₁ и V₂.

Изменением частоты ГВЧ или ёмкости конденсатора С_обр можно настроить колебательный контур в резонанс. Из теории электрических

Рис. 2.11. Принцип действия измерителя добротности

цепей известно, что при резонансе напряжение на конденсаторе и на индуктивности оказывается в Q раз больше, чем напряжение питания U₁. Здесь Q - добротность контура

Q = 1/ ωС_обр R_l (2.6)

или

Q = wL / R_L . (2.7)

Измерение индуктивности производится следующим образом: катушка, индуктивность L_x которой необходимо измерить, подсоединяется к зажимам L и при заданной частоте питания f контур настраивается в резонанс изменением ёмкости С_обр. При резонансе отклонение стрелки вольтметра V₂ будет максимальным. Приравняв (2.6) и (2.7) , получим

^Lx = 1/w²Cобр

где значение С_обр отсчитывается по шкале конденсатора переменной ёмкости.

При измерении ёмкости к зажимам L подсоединяется образцовая катушка индуктивности L_o₆_p и измерение выполняется в два этапа. Вначале изменением частоты генератора контур L^ С_обр настраивается в резонанс. Резонансная частота в этом случае

fрез = 1/(2пV^квLобрCобр₁). (2.8)

Далее конденсатор, емкость которого С_х необходимо измерить, подключается параллельно конденсатору С_обр и, не меняя частоты генератора, контур снова настраивают в резонанс изменением ёмкости образцового конденсатора. Так как резонансная частота (частота питающего напряжения) не изменилась, то

fрез = 1/2пV^квL_o₆_p (С_о6р2+ Сх). (2.9)

Приравняв (2.8) и (2.9), получим

^Сх = ^Собр1 ^— Собр₂.

При измерении добротности контура она может быть определена по показаниям вольтметров

Q = U2/U1.

Если поддерживать напряжение питания U₁ постоянным, то очевидно, что шкала вольтметра V₂ может быть проградуирована непосредственно в единицах добротности. Выпускаемые промышленностью измерители добротности обеспечивают проведение измерений на частотах от 1 кГц до 300 МГц с погрешностью в пределах 0,5 ... 5%.

ЛЕКЦИЯ №6

2. СРЕДСТВА ИЗМЕРЕНИЯ И КОНТРОЛЯ РАЗМЕРОВ И ПЕРЕМЕЩЕНИЙ

Линейные и угловые размеры, перемещения принято относить к первой группе механических величин. Как правило, это изометрические параметры различных деталей в обрабатывающей промышленности, характеристики профилей и шероховатостей поверхностей, уровни сыпучих веществ и жидкостей в различных сосудах (баках, танкерах, паровых котлах и т.п.), перемещения режущего инструмента относительно обрабатываемой детали, параметры износа трущихся частей различных механизмов, биения валов, расстояния и т.д.

Диапазон, охватываемый величинами этой группы, простирается от долей микрона до тысяч метров, т. е. составляет примерно десять порядков. Диапазон угловых размеров равен 3-4 порядкам.

Ко второй группе относятся различного рода силовые воздействия. Это механические напряжения в деталях и конструкциях машин и сооружений, силы, крутящие моменты, давления жидкостей и газов, акустические шумы, разности давлений и т. п.

Диапазоны значений величин этой группы, как правило, весьма широки. Например, в вакуумной технике приходится измерять давления до 1,3-10^-8 Па (10^-10 мм рт. ст.), а в технике высоких давлений до 10⁸ Па и выше, следовательно, диапазон давлений охватывает 16 порядков. Примерно такой же диапазон занимают значения сил, встречающихся в технике и научных исследованиях (10^-8 ... 10⁸ Н).

Третью группу механических величин представляют так называемые параметры движения. Это перемещения объектов в пространстве, линейные и угловые скорости и ускорения перемещений. Значения параметров этой группы могут достигать астрономических цифр (космические расстояния и скорости). В эту группу входят также параметры вибраций (вибрационные перемещения, скорости и ускорения), скорости вращения валов и т. д.

2.1. МЕХАНИЧЕСКИЕ СРЕДСТВА ИЗМЕРЕНИЯ

Конструкция подавляющего большинства механических средств измерения состоит из последовательно расположенных элементов и устройств, каждое из которых в этой последовательности выполняет определённую задачу при измерении. Для того чтобы в дальнейшем при изучении средств измерения было легче представлять их действие, рассмотрим коротко эти устройства и их назначения.

Основание измерительного средства - это конструктивный элемент, на базе которого смонтированы все элементы данного действующего средства измерения. Например, штанга штангенциркуля, скоба микрометра, корпус индикатора часового типа.

Воспринимающий элемент - это часть средства измерения, которая осуществляет его соприкосновение с объектом измерения и воспринимает величину этого объекта, например измерительные губки штангенциркуля, измерительный наконечник индикатора. Часть воспринимающего элемента, непосредственно касающаяся поверхности объекта, иногда называют чувствительным элементом.

Размерный элемент - это одна из деталей средства измерения, которая обладает собственным точным, обычно многозначным, размером, с величиной которого в процессе измерения непосредственно сопоставляется воспринятая средством измерения величина объекта измерения (например, штанга со шкалой штангенциркуля: размер детали, воспринятый губками, сравнивается с ней ).

⇐ Предыдущая 1 2 345 6 7 8 Следующая ⇒