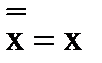- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Функцияның ақиқаттық кестесі
Функцияның ақиқаттық кестесі
НЕМЕСЕ элементінің
| X1 |
| X2 |
| Х1 v Х2 |
| x1 | x2 | f(x1\/x2) |
Дизъюнктор
3. Логикалық көбейту (конъюнкция – AND – И – ЖӘНЕ, (белгілеу түрлері: /\, &, *, ∩). Бұл бірнеше айнымалының функциясы. Функция келесі түрде белгіленеді: f(x1x2) = x1 /\ x2 /\ х3 …
Функцияның ақиқаттық
кестесі
ЖӘНЕ элементтің графикалық белгіленуі:
| x1 | x2 | f(x1/\x2) |
| Х1 /\ Х2 |
| & |
| X1 |
| X2 |
конъюнктор
4. Шеффер функциясы – кері көбейтуді жүзеге асырады. Бұл бірнеше айнымалылар функциясы. Функция келесі түрде болады ( | - Шеффер штрихыдеп аталады):
(x1x2) = x1½x2 = x1 /\ x2
| Функцияның ақиқаттық кестесі | ЖӘНЕ – ЕМЕС элементінің графикалық белгіленуі | |||||||||||||||||||
|
|
5. Пирс функциясы логикалық кері қосуды жүзеге асырады. Бұл бірнеше айнымалылар функциясы. Функция келесі түрде болады (↓ – Пирс бағыттауышы деп аталады):
f(x1x2) = x1 ¯ x2 = x1 Ú x2
| Функцияның ақиқаттық кестесі | НЕМЕСЕ-ЕМЕС элементінің графикалық белгіленуі | |||||||||||||||||||
|
|
6. mod 2 бойынша қосу. XOR логикалық операцияны орындайды. Бұл бірнеше айнымалылар функциясы және функция келесі түрде болады:
Y = x1 Å x2
| Функцияның ақиқаттық кестесі | XOR -элементінің графикалық белгіленуі: | |||||||||||||||||
|
=1
|
2.1-кесте – Логикалық алгебраның негізгі заңдары
| Заң | НЕМЕСЕ үшін | ЖӘНЕ үшін |
| Ауыстырымдылық заңы. Коммутативтілік (латын тілінен аударғанда – ауыстыру, алмастыру) | X1 \/ X2 = X2 \/ X1 | X1 /\ X2 = X2 /\ X1 |
| Біріктіру заңы. Ассоциативтілік (латын тілінен аударіанда – қосу, біріктіру, үйлестіру). | X1 \/ (X2\/ X3) = (X1 \/ X2) \/ X3 | X1 /\ (X2 /\ X3) = = (X1 /\ X2) /\ X3 |
| Тарату заңы. Дистрибутивтілік (латын тілінен аударғанда – тарату, үйлестіру) | X1 /\ (X2\/ X3) = (X1 /\ X2) \/ (X1\/ X3) | X1 \/ (X2 /\ X3) = = (X1 \/ X3) /\ (X1 \/ X3) |
| Де Морган ережесі |
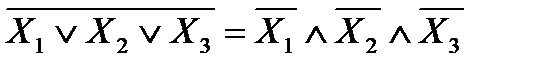
|
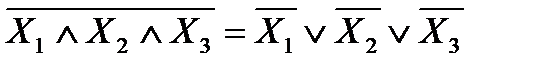
|
| Жойылу заңы. Идемпотенттілік (латын тілінен аударғанды – өшу, жойылу) | 
| |
| Шағылысу (жұтылу) заңы | X1 \/ (X1 /\X2) = X1 | X1 /\ (X1 \/ X2) = X1 |
| Жабыстыру заңы |
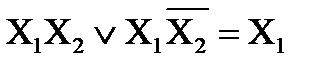
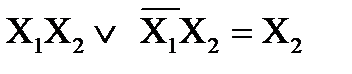
| (X1\/X2)(X1\/X2) = X1 (X1\/X2)(X1\/X2) = X1 |
| Айнымалы мен оның керісіне орындалатын амал. Комплементарлық заң (латын тілінен аударғанда– толықтыру) | х \/ х =1 | х /\ х = 0 |
| Тұрақтылар қасиеті | 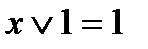 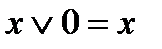
|
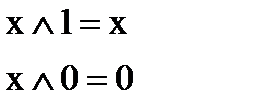
|
| Екі рет терістеу амалы |
| |
Кестеде логикалық операциялардың орындалу басымдылығы көрсетілген.
2.2-кесте – Логикалық амалдардың орындалу басымдылығы
| басымдылығы | операция |
| инверсия конъюнкция дизъюнкция mod 2 бойынша қосу |
Басымдылықтары бірдей операциялар солдан оңға қарай орындалады. Операциялардың орындалу ретін өзгерту үшін жақшаларды қолдануға болады. Жақшалардағы операциялар бірінші орындалады.
Мысал. Кез келген “n” айнымалы логикалық функциясы кесте түрінде берілуі мүмкін, ол кестенің сол жақ бөлігінде айнымалы мәндерінің барлық 2n жиынтығы, ал оң жақ бөлігінде осы жиынтықтардағы функция мәндері келтіріледі.
Мысалы: 3 айнымалы үшін мына кестедегідей болады:
2.3-кесте – 3 айнымалы үшін логикалық функция кестесі
| x1 | x2 | x3 | ƒ |
ƒ=1 болғандағы функциядағы х жиынтығын (жолдар) бірлік жиынтық деп, ал бірлік жиынтықтар жиынын ƒ – тің бірлік жиыны деп атайды.
ƒ=0 болғандағы х жиынтығын ƒ – тің нөлдік жиынтығы деп атайды.
Мәндер кестесінен логикалық функцияны құрамыз. Ол үшін функция бірге тең болған жолдағы аргументтердің конъюнкциясын аламыз. Егер аргумент нөлге тең болса, ол инверсиямен алынады. Алынған конъюнкцияны дизъюнкциямен біріктіреміз. Біздің мысалымыз үшін үш конъюнкция берілген (кестенің үш жолында функцияның мәні бірге тең). Логикалық функция мына түрде болады:
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|