
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Арифметические операции 2 страница
0 - 0 = 02; 0 - 1 = 12; 1 - 0 = 12; 1 - 1 = 02.
При вычитании 0 - 1 = 12 производится заем в текущий бит.
Арифметическое умножение одноразрядных двоичных чисел выполняется по следующим правилам:
0 × 0 = 02; 0 × 1 = 02; 1 × 0 = 02; 1 × 1 = 02.
Арифметическое сложение, вычитание, умножение и деление многоразрядных двоичных чисел будет рассмотрено ниже.
2.3. Представление информации в вычислительно технике
Минимальной единицей информации является один бит (один двоичный разряд). В вычислительной технике двоичные числа не зависимо от своего значения имеют фиксированную длину, называемую разрядной сеткой. Разрядность сетки может составлять 8, 16, 32, 64, 128 бит. Обычно разрядность сетки соответствует разрядности рабочих регистров микропроцессора. Информационные единицы, записанные в соответствующих разрядных сетках, имеют следующие названия:
Байт = 8 бит.
Слово = 2 байта = 16 бит.
Двойное слово = 2 слова = 4 байта = 32 бита.
Четверное слово = 4 слова = 8 байт = 64 бита.
Двоичное число, полученное при переводе из десятичной системы счисления, может иметь произвольное количество разрядов, поэтому его необходимо выровнять по границе заданной разрядной сетки.
Запись двоичного числа в восьмиразрядной сетке выполняется в следующей последовательности:
Определить количество разрядов двоичного числа.
Дописать слева нули, чтобы общее количество разрядов было равно восьми.
Запись двоичного числа в шестнадцатиразрядной сетке выполняется в следующей последовательности:
Определить количество разрядов двоичного числа.
Дописать слева нули, чтобы общее количество разрядов было равно шестнадцати.
Если количество полученных при переводе разрядов двоичного числа больше длины разрядной сетки, то данное число не входит в заданный диапазон.
При проектировании вычислительных устройств выбирается способ представления в машине положительных и отрицательных чисел. Для представления положительных двоичных чисел в машине применяют обычный (натуральный) код. Для представления отрицательных двоичных чисел в машине применяют специальные коды: прямой, обратный, дополнительный и смещенный коды.
Положительные числа в прямом, обратном и дополнительном кодах соответствуют натуральному, а отрицательные имеют различный вид. В этих кодах предусматривается старший (левый) разряд сетки для представления знака числа, причем знак «+» кодируется цифрой 0, а знак - цифрой 1.
Изменение знака числа с плюса на минус выполняется следующим образом:
Прямой код: в знаковом разряде натурального числа ноль заменяется на единицу.
Обратный код:
2.а. В знаковом разряде натурального числа ноль заменяется на единицу.
2.б. В остальных разрядах выполняется поразрядная инверсия (все нули заменяются на единицы, а единицы – на нули).
Дополнительный код:
3.а. В знаковом разряде натурального числа ноль заменяется на единицу.
3.б. В остальных разрядах выполняется поразрядная инверсия.
3.в. К полученному двоичному числу прибавляется единица по правилам арифметического сложения.
Изменение знака числа с минуса на плюс выполняется следующим образом:
Прямой код: в знаковом разряде натурального числа единица заменяется на ноль.
Обратный код:
2.а. В знаковом разряде натурального числа единица заменяется на ноль.
2.б. В остальных разрядах выполняется поразрядная инверсия (все нули заменяются на единицы, а единицы – на нули).
Дополнительный код:
3.а. В знаковом разряде натурального числа единица заменяется на ноль.
3.б. В остальных разрядах выполняется поразрядная инверсия.
3.в. К полученному двоичному числу прибавляется единица по правилам арифметического сложения.
Натуральный двоичный код положительного десятичного числа +110 равен 000000012. В таблице приведены прямой, обратный и дополнительные коды отрицательного числа -110.
Табл. Прямой, обратный и дополнительные коды числа -110
| Прямой код числа -110 | 100000012 |
| Обратный код числа -110 | 111111102 |
| Дополнительный код числа -110 | 111111112 |
Смещенный код используется в вычислительной машине для упрощения операций вычисления и сравнения над положительными и отрицательными порядками дробных чисел (чисел с плавающей точкой). Смещенный порядок вычисляется как сумма порядка числа с константой (смещением). Константа представляет собой значение смещенного нулевого порядка (обычно 12710 или 102310).
В таблице приведены примеры вычисления положительного и отрицательного порядков.
Табл. Порядок определения смещенного кода
| Константа | Порядок | Смещенный порядок | Результат |
| 12710 = 011111112 | 010 | 12710 + 010 = 12710 = 011111112 | Смещенный нулевой порядок |
| 12710 = 011111112 | +110 | 12710 + 110 = 12810 = 100000002 | Смещенный +1-ый порядок |
| 12710 = 011111112 | -110 | 12710 + (- 110) = 12610 = 011111102 | Смещенный -1-ый порядок |
В вычислительной технике используются следующие форматы данных, которые могут храниться указанных в различных разрядных сетках:
Целые числа без знака (unsigned).
Целые числа со знаком (signed).
Числа с плавающей точкой (float).
Символьные данные (char).
Двоично-десятичные числа (BCD).
2.3.1. Целые числа без знака (unsigned)
Целые числа без знака используются для представления только положительных чисел. Количество двоичных чисел, которые могут быть представлены с помощью n-разрядов равно 2n. Диапазон представления целых чисел без знака определяется как 0 … 2n-1, где n – длина разрядой сетки.
Табл.2.14. Диапазон целых чисел без знака
| Тип данных | Размер n, бит | Диапазон 0 … 2n-1 | |
| Dec | Hex | ||
| unsigned (short) char | 0 … 255 | 00 … FF | |
| unsigned int | 0 … 65535 | 0000 … FFFF | |
| unsigned long | 0 … 4294967295 | 00000000 … FFFFFFFF | |
Пример: Перевести целое десятичное число 12510 в двоичную систему счисления. Двоичное число записать восьмиразрядной и шестнадцатиразрядной сетках.
Перевод числа 12510 = 11111012.
Число 12510 входит в диапазон чисел 0 … 255 и 0 … 65535.
Ответ: 1. Для n=8 число 12510 = 0111 11012; 2. Для n=16 число 12510 = 0000 0000 0111 11012 (здесь и далее в записи двоичного числа используем пробел между тетрадами для контроля разрядности числа).
Пример: Перевести целое десятичное число 25610 в двоичную систему счисления. Двоичное число записать восьмиразрядной и шестнадцатиразрядной сетках.
Перевод числа: 25610 = 1 0000 00002.
Число 25610 не входит в диапазон чисел 0 … 255 и входит в диапазон чисел 0 … 65535.
Ответ: 1. Число 25610 нельзя представить в восьмиразрядной сетке, т.к. оно не входит в диапазон 0 … 255; 2. Для n=16 число 25610 = 0000 0001 0000 00002.
Пример: Определить знак двоичного числа 10000000000000002.
Ответ: Двоичное число является положительным, так как в формате без знака все числа положительные.
2.3.2. Целые числа со знаком (signed)
Целые числа со знаком используются для представления как положительных, так и отрицательных чисел. Диапазон представления целых чисел со знаком определяется как 2n-1 … 2n-1-1, где n – количество разрядов сетки.
Табл.2.15. Диапазон целых чисел со знаком
| Тип данных | Размер n, бит | Диапазон 2n-1 … 2n-1-1 | |
| Dec | Hex | ||
| signed (short) char | -128 … +127 | 00 … FF | |
| signed int | -32 768 … +32 767 | 0000 … FFFF | |
| signed long | -2 147 483 648 … +2 147 483 647 | 8000 0000 … 7FFF FFFF | |
Для изображения знака числа в разрядной сетке используется старший (левый) разряд, в котором 0 соответствует положительному числу, 1 - отрицательному. Для восьмиразрядной сетки знаковым является седьмой разряд, для шестнадцатиразрядной сетки знаковым является пятнадцатый разряд.
Табл. 2.15.1. Положительное двоичное восьмиразрядное число
Табл. 2.15.2. Отрицательное двоичное восьмиразрядное число
Для кодирования чисел со знаком в микропроцессорной технике применяется специальный двоичный дополнительный код, который обладает следующими свойствами:
Дополнительные коды положительных двоичных чисел формата signed определены в диапазоне 0 … 2n-1-1 и совпадают с двоичными кодами чисел формата unsigned, определенных в диапазоне 0 … 2n-1-1. Дополнительные коды положительных двоичных чисел получаются делением на 2.
Дополнительный код отрицательного двоичного числа определяется двумя способами:
По формуле Х10 = [2n + Х10]2 , где Х10 – отрицательные десятичные числа в диапазоне от (-1) до (-2n/2).
По правилу изменения знака двоичного числа в дополнительном коде:
2.2.1. Записать двоичное число в заданной разрядной сетке.
2.2.2. Заменить в двоичном числе все нули на единицы, а единицы на нули (поразрядная инверсия).
2.2.3. Полученное число сложить с единицей по правилам двоичной арифметики.
Данное правило может применяться для перехода от положительных двоичных чисел к отрицательным числам, и наоборот.
Изменение знака шестнадцатеричного числа 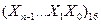 выполняется в следующей последовательности:
выполняется в следующей последовательности:
1. Выполнить поразрядную инверсию каждого символа 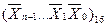 по формуле [24 - 1 - Хi]16.
по формуле [24 - 1 - Хi]16.
2. Полученное шестнадцатеричное число сложить с единицей по правилам двоичной арифметики 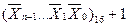 .
.
Способ перевода двоичных чисел со знаком в десятичную систему счисления зависит от знака числа:
1. Целые положительные двоичные числа переводятся по формуле степенного ряда вида:
an-1×рn-1 + an-2×рn-2 + . . . + a1×р1 + a0×р0.
2. Целые отрицательные двоичные числа переводятся по формуле степенного ряда вида:
(-an-1)×рn-1 + an-2×рn-2 + . . . + a1×р1 + a0×р0, где (n-1) – старший разряд разрядной сетки.
Пример. Представить число +12510 в восьмиразрядной и шестнадцатиразрядной сетках.
Число +12510 входит в диапазон чисел (-128 … +127) и (-32768 … +32767).
Ответ: 1. Для n=8 число 12510 = 0111 11012; 2. Для n=16 число 12510 = 0000 0000 0111 11012.
Пример: Определить знак двоичного числа 0111 11012 в восьмиразрядной сетке.
Число 0111 11012 записано в восьмиразрядной сетке.
Ответ: Число 0111 11012 положительное, т.к. в старшем 7-ом знаковом разряде записан ноль.
Пример: Определить знак двоичного числа 0000 0000 0111 11012 в шестнадцатиразрядной сетке.
Число 0000 0000 0111 11012 записано в шестнадцатиразрядной сетке.
Ответ: Число 0000 0000 0111 11012 положительное, т.к. в старшем 15-ом знаковом разряде записан ноль.
Пример. Представить число -12510 в восьмиразрядной и шестнадцатиразрядной сетках.
Число -12510 входит в диапазон чисел (-128 … +127) и –(32768 … +32767).
Для n=8 d10 = -12510 = [28 -12510]2 = [256 -12510]2 =[13110]2 = 100000112.
Для n=16 d10 = -12510 = [216 -12510]2 = [65536 -12510]2 =[6541110]2 = 1111 1111 1000 00112.
Ответ: для n=8 -12510 = 1000 00112 ; для n=16 -12510 = 1111 1111 1000 00112.
Пример: Представить двоичное число 0111 11012 в десятичной системе счисления.
Для положительного числа используем формулу:
a7×р7 + a6×р6 + a5×р5 + a4×р4 + a3×р3 + a2×р2 + a1×р1 + a0×р0 = 0+64+32+16+8+4+0+1 = 12510.
Ответ: число 0111 11012 = +12510.
Пример: Представить двоичное число 0111 11012 в шестнадцатеричной системе счисления.
Ответ: число 0111 11012 = 7D16.
Пример: Определить знак шестнадцатеричного числа 7D 16.
Ответ: числа 7D16 положительное, т.к. в старшем разряде числа 7D16 цифра 716 = 01112, старший бит тетрады равен 02, что соответствует знаку плюс.
Пример: Изменить знак двоичного числа 111 11012 и записать число в восьмиразрядной сетке.
1. Записываем 111 11012 число в восьмиразрядной сетке 0111 11012.
2. Число 0111 11012 положительное, т.к. в старшем 7-ом знаковом разряде записан ноль.
2. Выполняем поразрядную инверсию 1000 00102.
3. Складываем число с единицей 1000 00102 + 0000 00012 = 1000 00112.
Ответ: полученное число 1000 00112 является отрицательным, т.к. в старшем 7-ом знаковом разряде записана единица.
Пример: Определить знак двоичного числа 1111 11012 в восьмиразрядной сетке.
Число 1111 11012 записано в восьмиразрядной сетке.
Ответ: Число 1111 11012 отрицательное, т.к. в старшем 7-ом знаковом разряде записана единица.
Пример: Определить знак двоичного числа 1000 0000 0111 11012 в шестнадцатиразрядной сетке.
Число 1000 0000 0111 11012 записано в шестнадцатиразрядной сетке.
Ответ: Число 1000 0000 0111 11012 отрицательное, т.к. в старшем 15-ом знаковом разряде записана единица.
Пример: Представить двоичное число 1000 00112 в десятичной системе счисления.
Для отрицательного числа используем формулу:
(-a7)×р7 + a6×р6 + a5×р5 + a4×р4 + a3×р3 + a2×р2 + a1×р1 + a0×р0 = -128+0+0+0+2+1 = -12510
Ответ: 1000 00112 = -12510.
Пример. Представить двоичное число 1000 00112 в шестнадцатеричной системе счисления.
Ответ: 1000 00112 = 8316.
Пример: Определить знак шестнадцатеричного числа 8316.
Ответ: число 8316 отрицательное, т.к. в старшем разряде числа 8316 цифра 816 = 10002, старший бит тетрады равен 12, что соответствует знаку минус.
Пример: Изменить знак двоичного числа 0111 11012 в шестнадцатиразрядной сетке.
1. Записываем 0111 11012 число в шестнадцатиразрядной сетке 0000 0000 0111 11012.
2. Выполняем поразрядную инверсию (заменяем все нули на единицы, а единицы - на нули) 1111 1111 1000 00102.
3. Складываем число с единицей
1111 1111 1000 00102 + 0000 0000 0000 00012 = 1111 1111 1000 00112.
Ответ: число 1111 1111 1000 00112.
Пример: Определить знак двоичного числа 1111 1111 1000 00112.
Двоичное число 1111 1111 1000 00112 записано в шестнадцатиразрядной сетке.
Ответ: Число 1111 1111 1000 00112 отрицательное, т.к. в старшем 15-ом знаковом разряде записана единица.
Пример: Представить двоичное число 1111 1111 1000 00112 в десятичной системе счисления.
Для отрицательного числа используем формулу:
(-a15)×р15+a14×р14+a13×р13+a12×р12+a11×р11+a10×р10+a9×р9+a8×р8+a7×р7+a6×р6+a5×р5+a4×р4+a3×р3+a2×р2
+a1×р1+a0×р0= = -32768+16384+8192+4096+2048+1024+512+256+128+0+0+0+2+1 = -12510
Ответ: 1111 1111 1000 00112 = -12510.
Пример: Представить двоичное число 1111 1111 1000 00112 в шестнадцатеричной системе счисления.
Ответ: 1111 1111 1000 00112 = FF8316
Пример: Определить знак шестнадцатеричного числа FF8316.
Ответ: числа FF8316 отрицательное, т.к. в старшем разряде символа F16 = 11112 старший бит тетрады равен 12.
Пример. Представить шестнадцатеричное число 7D16 в двоичной системе счисления.
Ответ: 7D16 = 0111 11012.
Пример. Представить шестнадцатеричное число 7D16 в десятичной системе счисления.
Число 7D 16 положительное, поэтому можно применить формулу степенного ряда: a1×р1+a0×р0.
7D 16 = (7)10 (13)10= 7×16р1+13×16р0 = 112 +13 = 12510.
Ответ: 7D16 = +12510.
Пример. Представить шестнадцатеричное число 8316 в двоичной системе счисления.
Ответ: 7D16 = 1000 00112.
Пример. Представить шестнадцатеричное число 8316 в десятичной системе счисления.
Число 8316 отрицательное, поэтому сначала нужно перевести в двоичную систему счисления и перевести по формуле (-a7)×р7 + a6×р6 + a5×р5 + a4×р4 + a3×р3 + a2×р2 + a1×р1 + a0×р0.
8316 = 1000 00112 = -128 + 2 +1 = -12510.
Ответ: 8316 = -12510.
2.3.3. Числа с плавающей точкой (float)
Формат чисел с плавающей точкой используется для вещественных (дробных) чисел.
Табл.2.16. Форматы чисел с плавающей точкой в стандарте IEEE 754
| Тип данных | Формат | Размер n, бит | Диапазон |
| float | Одинарная точность | 3.4E-38 … 3.4E+38 | |
| double | Двойная точность | 1.7E-308 … 1.7E+308 | |
| long double | Повышенная точность | 3.4E-4932 … 3.4E+4932 |
Формат 32-разрядного двоичного числа с плавающей точкой приведен в табл2.17.
Табл.2.17. Структура 32-разрядного двоичного формата с плавающей точкой
| +/- | Смещенный порядок, 8 бит | Мантисса, 23 бита | |||||||||||||||||||||||||||||
Примечание: бит 31 – знак числа.
Пример: Представить положительное вещественное десятичное число +125,5710 в 32-разрядном двоичном формате (float) с плавающей точкой.
Для представления положительного числа в формате с плавающей точкой выполняются следующие операции:
А) Перевод целой части десятичного числа: 12510 = 11111012.
Б) Перевод дробной части десятичного числа: 0,5710 = 0,100100012
В) Запись двоичного числа в формате с фиксированной точкой: 125,5710 = 1111101,100100012.
Г) Нормализация числа c фиксированной точкой.
Нормализованное число – это число, записанное в экспоненциальном виде. Нормализация выполняется сдвигом точки (запятой) вправо или влево до позиции, в которой в целой части остается одна значащая единица. В результате получается нормализованное двоичное число с порядком:
1111101,100100012 = 1,111101100100012 ∙ 26 (порядок числа равен 6).
Д) Определение знака, мантиссы и смещенного порядка
Знак числа 125,5710 положительный, поэтому в знаковом 31-ом разряде записывается 0 (ноль).
Мантисса представляет собой дробную часть нормализованного числа: 11110110010001 (целая часть нормализованного числа не записывается и не сохраняется в памяти).
Смещенный порядок определяется как сумма нулевого смещенного порядка и порядка нормализованного числа.
В стандарте IEEE 754 нулевой смещенный порядок равен 12710 = 0111 11112.
Порядок нормализованного числа равен 610.
Рассчитываем смещенный порядок: 12710 + 610 = 13310.
Получаем шестой смещенный порядок равный 13310 = 1000 01012.
Е) Запись нормализованного числа в формате с плавающей точкой приведена в табл.2.18.1.
Табл.2.18.1. Число 125,5710 в формате с плавающей точкой
| + | смещенный порядок | мантисса | |||||||||||||||||||||||||||||
Ответ: десятичное число 125,5710 в формате с плавающей точкой имеет вид:
0 10000101 111100110010001111000002.
Пример: Представить отрицательное вещественное десятичное число -125,5710 в 32-разрядном двоичном формате (float) с плавающей точкой. Отрицательные числа с плавающей точкой представляются прямым кодом:
Для представления отрицательного числа в формате с плавающей точкой выполняются следующие операции:
А) Перевод целой части десятичного числа, взятого по модулю: [12510] = 11111012.
Б) Перевод дробной части десятичного числа, взятого по модулю: [0,5710] = 0,100100012
В) Запись двоичного числа в формате с фиксированной точкой: 125,5710 = 1111101,100100012.
Г) Нормализация числа c фиксированной точкой.
Нормализованное число – это число, записанное в экспоненциальном виде. Нормализация выполняется сдвигом точки (запятой) вправо или влево до позиции, в которой в целой части остается одна значащая единица. В результате получается нормализованное двоичное число с порядком:
1111101,100100012 = 1,111101100100012 ∙ 26 (порядок числа равен 6).
Д) Определение знака, мантиссы и смещенного порядка
Знак числа -125,5710 отрицательный, поэтому в знаковом 31-ом разряде записывается 1 (единица).
Мантисса представляет собой дробную часть нормализованного числа: 11110110010001 (целая часть нормализованного числа не записывается и не сохраняется в памяти).
Смещенный порядок определяется как сумма нулевого смещенного порядка и порядка нормализованного числа.
В стандарте IEEE 754 нулевой смещенный порядок равен 12710 = 0111 11112.
Порядок нормализованного числа равен 610.
Рассчитываем смещенный порядок: 12710 + 610 = 13310.
Получаем шестой смещенный порядок равный 13310 = 1000 01012.
Е) Запись нормализованного числа в формате с плавающей точкой приведена в табл.2.18.2.
Табл.2.18.2. Число -125,5710 в формате с плавающей точкой
| - | смещенный порядок | мантисса | |||||||||||||||||||||||||||||
Ответ: десятичное число -125,5710 в формате с плавающей точкой имеет вид:
1 10000101 111100110010001111000002.
2.3.4. Символьные данные (char)
Каждый символ в микропроцессорной технике кодируется целым числом. К символам относятся: цифры, прописные буквы, строчные буквы, знаки пунктуации, арифметические знаки, пробел, управляющие символы и др. Представление символа в виде целого числа называется кодом символа.
Коды символов используются для хранения, ввода/вывода, хранения и обмена информацией.
Существуют следующие системы кодирования:
- КОИ-7 (Код Обмена Информацией, 7 бит);
- ASCII (American Standard Code for Information Interchange – стандартный код для обмена информацией, 7бит);
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|