
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Арифметические операции 1 страница
2. Арифметические основы микропроцессорной техники
2.1. Системы счисления
Системой счисления называется совокупность правил записи чисел с помощью символов. Различают непозиционные (римские цифры) и позиционные (десятичная, двоичная и др.) системы счисления. Наиболее часто используются позиционные системы счисления, т.к. они позволяют выполнять арифметические операции.
Каждая позиционная система счисления характеризуется основанием. Основание системы счисления «р» - это количество символов, которое используется для изображения чисел.
В любой позиционной системе счисления целое число может быть представлено в двух формах записи:
- В виде последовательности символов an-1 an-2 . . . a1 a0 ,
- В виде степенного ряда
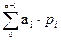 =
=
= an-1×рn-1 + an-2×рn-2 + . . . + a1×р1 + a0×р0 = an-1×qn-1 + an-2×qn-2 + . . . + a1×q1 + a0×q0 .
где an-1 - символ старшего разряда; a0 - символ младшего разряда; ai – символ i-го разряда; i – номер разряда (i = n-1, n-2, … 1, 0); n – количество разрядов числа; р – основание системы счисления; рi = qi – вес i-го разряда.
В позиционных системах счисления номера символов увеличиваются справа налево от младшего нулевого разряда до старшего (n-1)-разряда. В позиционных системах счисления значение символа зависит от его позиции в числе. Все разряды числа отличаются друг от друга весом или весовым коэффициентом qi=pi. Веса разрядов увеличиваются справа налево (от младшего к старшему) в «р»-раз.
В человеческой деятельности обычно используется десятичная система счисления.
Десятичная или децимальная (decimal, dec) система счисления имеет основание десять (р=10). Любое число записывается с помощью десяти символов (цифр): 0, 1, 2, 3, 4, 5, 6, 7, 8, 9.
Табл.2.1. Веса разрядов восьмиразрядного десятичного целого числа
| Номер разряда | ||||||||
| Вес разряда | 107 | 106 | 105 | 104 | 103 | 102 | 101 | 100 |
| Вес разряда |
Для отличия одной системы счисления от другой справа пишется символ, равный основанию 12510. Пример записи десятичного числа: 12510.
Пример записи десятичного числа:
в виде последовательности символов 125;
в виде степенного ряда 1·102 + 2·101 + 5·100 = 100 + 20 + 5.
В вычислительной технике для хранения, обработки и передачи информации (адресов, команд и данных) используется двоичная система счисления.
Двоичная или бинарная (binary, bin) система счисления имеет основание два (р=2). Любое число записывается с помощью двух символов (цифр): 0, 1. Эти двоичные цифры названы битами (bit от binary digit). Для идентификации двоичных чисел используются следующие способы: 11012, 1101bin, 1101b, 0b1101.
Табл.2.2. Веса разрядов восьмиразрядного двоичного целого числа
| Номер разряда | ||||||||
| Вес разряда | 27 | 26 | 25 | 24 | 23 | 22 | 21 | 20 |
| Вес разряда |
Пример записи двоичного целого числа:
в виде последовательности символов 1112;
в виде степенного ряда 1·(102)2 + 1·(102)1 + 1·(102)0 = 1002 + 102 + 12 (показатель степени для удобства приведен в десятичной системе счисления).
Цифровая и микропроцессорная техника строится в ИС ТТЛ (интегральные схемы транзисторно-транзисторной логики) и ИС КМОП (интегральные схемы комплементарные-металл-оксидные-полупроводниковые).
Напряжение питания ИС ТТЛ равно Uпит = +5,0 B. Уровни логических сигналов (биты) ИС ТТЛ на физическом уровне представляются напряжением питания Uпит в диапазоне от 0 до +5 В:
1. Биту, имеющему значение ноль (логический ноль, Low), соответствует напряжение низкого уровня U0 = (0 … +0,4) В.
2. Биту, имеющему значение единица (логическая единица, High) , соответствует напряжение высокого уровня U1 = (+2,4 В … +5,0) B.
Для питания различных ИС КМОП могут использоваться напряжения питания Uпит в диапазоне от 3,3 В до +15 В. Уровни логических сигналов (биты) ИС КМОП на физическом уровне представляются напряжением питания Uпит в диапазоне от 0 до + Uпит:
1. Биту, имеющему значение ноль (логический ноль, Low), соответствует напряжение низкого уровня U0 = (0 … +0,3∙Uпит) В.
2. Биту, имеющему значение единица (логическая единица, High) , соответствует напряжение высокого уровня U1 = (+0,99∙Uпит … Uпит) В.
В современных микропроцессорах, построенных на микросхемах КМОП, используется напряжение питания Uпит = 3,3 В и ниже.
Достоинства двоичной системы счисления:
Простота технической реализации цифровых элементов, используемых для построения вычислительной системы.
2) Высокая скорость обработки данных.
Недостатки двоичной системы счисления:
1) Трудность запоминания человеком двоичных чисел.
2) Большая разрядность двоичных чисел, по сравнению с другими системами счисления.
Для компактной записи двоичных чисел используются шестнадцатеричные числа.
Шестнадцатеричная или гексадецимальная (hexadecimal) система счисления имеет основание шестнадцать (р=2n=16, где n = 4 двоичных бита для записи каждого шестнадцатеричного символа). Для записи числа используются шестнадцать символов (цифр и букв): 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F. Значение каждой прописной буквы латинского алфавита буквы A, B, C, D, E, F соответствует десятичным числам 10, 11, 12, 13, 14, 15.
Каждый шестнадцатеричный символ может быть представлен единственным сочетанием четырех бит (тетрадой). Тетрада может принимать 24=16 значений (от 010 до 1510 или от 016 до F16). Шестнадцатеричная система используется для кодирования двоичных чисел, разрядность которых кратна четырем (4, 8, 16 и т.д.). Пример записи шестнадцатеричного числа: А516, А5hex, А5h, $А5, 0xА5.
Табл.2.4. Веса разрядов восьмиразрядного шестнадцатеричного целого числа
| Номер разряда | ||||||||
| Вес разряда | 167 | 166 | 165 | 164 | 163 | 162 | 161 | 160 |
| Вес разряда |
В таблице 2.5 представлены последовательности целых чисел, записанных в различных системах счисления.
Табл.2.5. Последовательности целых чисел в разных системах счисления
| Dec | Bin | Hex | Dec | Bin | Hex | Dec | Bin | Hex | Dec | Bin | Hex |
| A В | C D E F |
Шестнадцатеричные числа имеют следующие преимущества перед двоичными и десятичными:
1. Шестнадцатеричное число дает более компактную запись двоичного числа.
2. Шестнадцатеричное число имеет более упорядоченную форму записи по сравнению с десятичным числом, способствующую лучшему запоминанию.
Табл.2.6. Сравнительная характеристика различных систем счисления
| Разрядность двоичного числа, n | Максимальное значение n-разрядного числа (2n-1) | ||
| Двоичное | Десятичное | Шестнадцатеричное | |
| F | |||
| 1111 1111 | FF | ||
| 1111 1111 1111 | FFF | ||
| 1111 1111 1111 1111 | FFFF | ||
| 1111 1111 1111 1111 1111 | FFFFF | ||
В любой позиционной системе счисления вещественное число может быть представлено в двух формах записи:
1. В виде последовательности символов an-1 an-2 . . . a1 a0 , a-1 a-2 …a-(m-1) a-m,
2. В виде степенного ряда 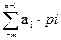 =
=
= an-1×рn-1 + an-2×рn-2 + . . . + a1×р1 + a0×р0 + a-1×р-1 + a-2×р-2 + … + a-(m-1)×р-(m-1) + a-m×р-m =
= an-1×qn-1 + an-2×qn-2 + . . . + a1×q1 + a0×q0 + a-1×q-1 + a-2×q-2 + … + a-(m-1)×q-(m-1) + a-m×q-m .
где ai – значение символа i-го разряда; i – номер разряда (i = n-1, n-2, … 1, 0, -1, -2 …, -m+1, -m); р – основание системы счисления; qi – вес i-го разряда (qi=рi); n – количество разрядов целой части вещественного числа; m – количество разрядов дробной части вещественного числа.
Пример записи десятичного вещественного числа:
в виде последовательности символов 125,87510;
в виде степенного ряда
1·102 + 2·101 + 5·100 + 8·10-1 + 7·10-2 + 5·10-3 = 10010 + 2010 + 510 + 0,810 + 0,0710. + 0,00510
Табл.2.7. Веса разрядов восьмиразрядного десятичного дробного числа
| Номер разряда | -1 | -2 | -3 | -4 | -5 | -6 | -7 | -8 |
| Вес разряда | 10-1 | 10-2 | 10-3 | 10-4 | 10-5 | 10-6 | 10-7 | 10-8 |
| Вес разряда | 0,1 | 0,01 | 0,001 | 0,0001 | 0,00001 | 0,000001 | 0,0000001 | 0,00000001 |
Пример записи двоичного вещественного числа:
в виде последовательности символов 1111101,1112;
в виде степенного ряда
1·(102)6 + 1·(102)5 + 1·(102)4 + 1·(102)3 + 1·(102)2 + 0·(102)1 + 1·(102)0 + 1·(102)-1 + 1·(102)-2 + 1·(102)-2 =
10000002 + 1000002 + 100002 + 10002 + 1002 + 02 + 12 + 0,12 + 0,012 + 0,0012
(показатель степени для удобства приведен в десятичной системе счисления).
Табл.2.8. Веса разрядов восьмиразрядного двоичного дробного числа
| Номер разряда | -1 | -2 | -3 | -4 | -5 | -6 | -7 | -8 |
| Вес разряда | 2-1 | 2-2 | 2-3 | 2-4 | 2-5 | 2-6 | 2-7 | 2-8 |
| Вес разряда | 1/2 | 1/4 | 1/8 | 1/16 | 1/32 | 1/64 | 1/128 | 1/256 |
2.2. Перевод из одной системы счисления в другую
2.2.1. Перевод целого десятичного числа в двоичную систему счисления
Перевод целого десятичного числа в двоичную систему счисления производят последовательным делением десятичного числа на основание двоичной системы счисления р=2.
Перевод выполняется по следующему правилу:
Разделить исходное десятичное число на 2.
Найти частное от деления.
Вычислить остаток, который является символом младшего 0-го разряда двоичного числа.
Разделить полученное частное от деления на 2.
Найти новое частное от деления.
Вычислить новый остаток, который является символом следующего разряда двоичного числа.
Проверить частное от деления:
- если частное от деления больше единицы, то перейти к пункту 4;
- если частное от деления равно единице, то перейти к пункту 8.
Частное от деления, равное единице, является старшим значащим разрядом двоичного числа.
Пример: Перевести целое десятичное число 12510 в двоичную систему счисления.
Порядок перевода приведен в таблице 2.1.1.
Табл.2.9. Перевод десятичного числа 12510 в двоичную систему счисления
| № | Деление | Частное от деления | Вычисление остатка | Остаток | Комментарий |
| 125 : 2 | 125 - (62×2) | 0-й (младший) разряд | |||
| 62 : 2 | 62 – (31×2) | 1-й разряд | |||
| 31 :2 | 31 – (15×2) | 2-й разряд | |||
| 15 : 2 | 15 – (7×2) | 3-й разряд | |||
| 7 :2 | 7 - (3×2) | 4-й разряд | |||
| 3 : 2 | 3 - (1×2) | 5-й разряд | |||
| 1 :2 | 6-й старший значащий разряд |
После перевода в столбике «Остаток» будет записано двоичное число, которое необходимо переписать в строчку снизу вверх слева направо, начиная со старшего значащего разряда.
Ответ: 12510 = 11111012.
2.2.2. Перевод целого двоичного числа в десятичную систему счисления
Перевод целого двоичного числа в десятичную систему счисления выполняется счисления по формуле степенного ряда an-1×рn-1 + an-2×рn-2 + . . . + a1×р1 + a0×р0 , где р=2. Перевод выполняется в следующей последовательности:
Записать формулу степенного ряда с учетом разрядности числа n.
Подставить в формулу значение битов двоичного числа.
Вычислить сумму членов степенного ряда.
Полученная сумма является десятичным эквивалентом двоичного числа.
Пример: Перевести двоичное число 11111012 в десятичную систему счисления. Для данного двоичного числа составляем степенной ряд, который будет использоваться для вычислений:
a6×р6 + a5×р5 + a4×р4 + a3×р3 + a2×р2 + a1×р1 + a0×р0 , где р=2.
Табл.2.10. Соответствие номера разряда и значения бита двоичного числа
| Номер бита, i | |||||||
| Бит ai | a6 | a5 | a4 | a3 | a2 | a1 | a0 |
| Значение бита ai |
Подставляем в формулу значение битов ai и основание системы счисления р=2
11111012 = 1·26 + 1·25 +1·24 + 1·23 + 1·22 + 0·21 + 1·20 = 64+32+16+8+4+0+1 = 12510.
Ответ: 11111012 = 12510.
2.2.3. Перевод целого двоичного числа в десятичную систему счисления суммированием весов единичных разрядов.
Перевод выполняется в следующей последовательности:
Найти в двоичном числе разряды (биты), равные единице.
Определить веса найденных единичных разрядов рi.
Сложить все веса единичных разрядов.
Пример: перевести двоичное число 11111012 в десятичную систему счисления.
Табл.2.11. Таблица соответствия номера разряда и веса разряда двоичного числа
| Номер бита, i | |||||||
| Вес бита, i | |||||||
| Значение бита ai | |||||||
| Вес единичного бита |
Складываем веса единичных (6, 5, 4, 3, 2 и 0)- разрядов: 64+32+16+8+4+0+1 = 12510.
Ответ: 11111012= 12510.
2.2.4. Перевод целого двоичного числа в шестнадцатеричную систему счисления
В шестнадцатеричной системе счисления каждый разряд представляется четырехразрядным двоичным числом, называемым тетрадой.
Перевод целого двоичного числа в шестнадцатеричную систему счисления производится по правилу:
Разбить двоичное число (справа налево) на тетрады (группы из четырех разрядов).
Дополнить старшую (левую) тетраду нулями, если после разбиения в ней оказывается меньше четырех разрядов.
Перевести каждую тетраду в десятичную систему счисления с помощью сложения весов единичных разрядов.
Преобразовать каждый десятичный символ в шестнадцатеричный (Табл.2.5).
Каждая тетрада после преобразования образует разряд шестнадцатеричного числа.
Пример: Перевести двоичное число 11111012 в шестнадцатеричную систему счисления.
11111012 = [111] [1101] = [0111] [1101]. Порядок перевода показан в таблице 2.4.
Табл.2.12. Перевод восьмиразрядного двоичного числа в шестнадцатеричное
| Тетрады | Старшая тетрада | Младшая тетрада | ||||||
| Вес тетрады | ||||||||
| Двоичное число | ||||||||
| Десятичное число | ||||||||
| Шестнадцатеричное число | D | |||||||
Ответ: 11111012 = 7D16.
2.2.5. Перевод целого шестнадцатеричного числа в двоичную систему счисления
Перевод шестнадцатеричного числа в двоичную систему счисления производят по правилу:
Каждый символ шестнадцатеричного числа переводится в десятичный.
Каждый десятичный символ переводится в тетраду.
Из последовательности тетрад составляется двоичное число.
Пример: Перевести шестнадцатеричное число 7D16 в двоичную систему счисления
7D16 = [7][D]=[7][13]= [0111] [1101] = 11111012.
Ответ: 7D16 = 11111012.
2.2.6. Перевод целого шестнадцатеричного числа в десятичную систему счисления
Перевод целого шестнадцатеричного числа в десятичную систему счисления производят по формуле степенного ряда: an-1×рn-1 + an-2×рn-2 + . . . + a1×р1 + a0×р0 , где р = 16.
Перевод выполняется в следующей последовательности:
Записать степенной ряд с учетом разрядности числа n.
Подставить в формулу значение разрядов шестнадцатеричного числа
Пример: Перевести шестнадцатеричное число 7D16 в десятичную систему счисления. Для шестнадцатеричного числа составляем степенной ряд, который будет использоваться для вычислений: a1×р1 + a0×р0.
7D16 = [7][D] = [7][13] = 7×161 + 13×160 = 112 + 13 = 12510.
Ответ: 7D16 = 12510.
2.2.7. Перевод дробного десятичного числа в двоичную систему счисления
Перевод дробного десятичного числа в двоичную систему счисления производят последовательным умножением десятичного числа на 2 (на основание двоичной системы счисления р=2).
Перевод выполняется по следующему правилу:
Умножить дробную часть на два;
Разбить полученное произведение на целую и дробную части
Целая часть произведения является символом старшего (левого, минус первого) разряда двоичного числа;
Умножить дробную часть произведения на два
Разбить полученное произведение на целую и дробную части
Целая часть произведения является символом следующего разряда двоичного числа;
Перейти к пункту 4.
Количество умножений зависит от заданной точности представления дробной части. Если при умножении произведение становится равным 0.0, то дробное число точно представляется в двоичной системе счисления. Если при умножении произведение не становится равным 0.0, то дробное число может быть представлено в двоичной системе счисления только приближенно. Относительную погрешность можно определить по формуле σ = (Хисх-Хвос)/Хисх (Хисх – исходное десятичное число, Хвос – восстановленное десятичное число, полученное переводом из двоичной системы счисления).
Пример: перевести дробное десятичное число 0,5710 в двоичную систему счисления с точностью до восьмого знака (m=8). Порядок перевода приведен в таблице 2.9.2.
Табл.2.13. Перевод дробного десятичного числа 0,5710 в двоичную систему счисления
| № | Умножение | Произведение | Дробная часть | Целая часть | Комментарий |
| 0,57 * 2 | 1,14 | 0,14 | -1-ый (старший) разряд | ||
| 0,14 * 2 | 0,28 | 0,28 | -2-ой разряд | ||
| 0,28 * 2 | 0,56 | 0,56 | -3-ий разряд | ||
| 0,56 * 2 | 1,12 | 0,12 | -4-ый разряд | ||
| 0,12 * 2 | 0,24 | 0,24 | -5-ый разряд | ||
| 0,24 * 2 | 0,48 | 0,48 | -6-ой разряд | ||
| 0,48 * 2 | 0,96 | 0,96 | -7-ой разряд | ||
| 0,96 * 2 | 1,92 | 0,92 | -8-ой разряд |
Ответ: 0,5710 = 0,100100012.
2.2.8. Перевод дробного двоичного числа в десятичную систему счисления
Перевод дробного двоичного числа в десятичную систему счисления по формуле степенного ряда a-1×р-1 + a-2×р-2 + … + a-(m-1)×р-(m-1) + a-m×р-m (р=2).
Пример: перевести двоичное число 0,100100012 в десятичную систему счисления.
Основание системы счисления р=2, а m=8 (дано 8 знаков после запятой)
a-1×р-1+a-2×р-2+a-3×р-3+a-4×р-4+a-5×р-5+a-6×р-6+a-7×р-7+a-8×р-8
Подставляем в формулу значение разряда, основание системы счисления и номер разряда
0,100100012=1×2-1+0×2-2+0×2-3+1×2-4+0×2-5+0×2-6+0×2-7+1×2-8=1/2+0+0+1/16+0+0+0+1/256=0,569810
Ответ: 0,100100012 = 0,569810 ≈ 0,5710.
2.2.9. Проверка погрешности представления дробного десятичного числа
Относительная погрешность δ рассчитывается по формуле:
δ = (Хи-Хв)/ Хи *100 %, где Хи - исходное десятичное число; Хв - восстановленное десятичное число (переведенное из двоичной системы в десятичную систему).
Пример: исходное значение дробного десятичного числа равно 0,5710. Дробное двоичное число, полученное переводом числа 0,5710 с точностью до восьмого разряда, равно 0,100100012. Восстановленное дробное десятичное число из 0,100100012 равно 0,569810
δ = (0,57 - 0,5698)/ 0,57*100 % = 0,035 %.
Ответ: Относительная погрешность представления равна δ =0,035 %.
2.2.10. Двоичная арифметика
Правила выполнения арифметических действий над двоичными числами задаются таблицами сложения, вычитания и умножения. Правила арифметики во всех позиционных системах аналогичны.
Арифметическое сложение одноразрядных двоичных чисел выполняется по следующим правилам:
0 + 0 = 02; 0 + 1 = 12; 1 + 0 = 12; 1 + 1 = 102; 1 + 1 + 1 = 112.
При сложении двух и трех единиц в двоичном разряде происходит перенос единицы (1) из текущего бита в следующий разряд (левый, более старший разряд). Перенесенная единица может складываться с битами следующего разряда.
Арифметическое вычитание одноразрядных двоичных чисел выполняется по следующим правилам:
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|