Методичні вказівки

⇐ ПредыдущаяСтр 6 из 6

і завдання до контрольних робіт з дисципліни

«Теорія механізмів і машин»,

розділ структурний аналіз механізмів, для студентів напряму 6.050503 «Машинобудування»

освітньо - кваліфікаційний рівень – бакалавр (спеціальний вид діяльності)

«Технічний сервіс будівельної техніки», форма навчання – денна

Одеса 2013

Затверджено

Вченою радою

Факультету Гідротехнічного і транспортного будівництва ОДАБА

Протокол № … від…………2013р.

Методичні вказівки розглянуті і рекомендовані до друку на засіданні

кафедри Підйомно-транспортних, будівельних і дорожніх машин.

Протокол №…. Від…………………2013р.

Укладач: к.т.н., доц. Мацей Р.О.

Рецензент:к.т.н.,проф.,зав.кафедри «Машинознавство та деталі машин»,

ОНПУ Мотулько Б.В.

Анотація

У методичних вказівках наводяться матеріали з вивчення однієї із основних загальноінженерних дисциплін - Теорії механізмів і машин (далі ТММ), яка розглядає будову і класифікацію механізмів, методи кінематичного і динамічного дослідження, проектування схем, які є загальними для механізмів і машин різного призначення.

Методичні вказівки присвячені структурному аналізу, де розкривається його мета - вивчення теорії будови механізмів, можливих їх видозмін при однаковому функціональному призначенні і класифікації механізмів. У методичних вказівках представлений значний обсяг теоретичних і практичних відомостей і рекомендацій щодо основних питань ТММ, пов'язаних із структурою механізмів. Викладання ряду положень в методичних вказівках супроводжується короткими і доступними поясненнями і рекомендаціями щодо їх вживання і включає детальну розробку всіх питань, вирішення яких необхідне для розуміння зв'язку теоретичних і практичних частин структурного аналізу механізмів. Викладені теоретичні положення супроводжуються розв'язанням завдань на прикладах машин і устаткування, що працюють в будівельній галузі. Значна увага приділена питанням властивостей механізмів, їх будові і взаємодії, а також зв'язку теоретичного апарату ТММ з реальною будовою машин і устаткуванням будівельної індустрії. Значна увага приділена класифікації механізмів за певними структурними ознаками, що полегшує їх подальше вивчення, оскільки кожен з таких класів має певний метод кінематичного і кинетостатичного дослідження.

Відповідальний за випуск:

зав. кафедрою підйомно-транспортних, будівельних і дорожніх машин

д.т.н., проф. Оргіян О. А.

ПРЕДМОВА

"Теорія механізмів і машин" є однією з базових дисциплін у підготовці інженерів за спеціальністю «Технічний сервіс будівельної техніки». Будучи науковою основою спеціальних дисциплін по подальшому вивченню будівельних машин і устаткування, вона розглядає загальні методи дослідження, розрахунку і проектування механізмів і машин незалежно від їх функціонального призначення. Не дивлячись на функціональні відмінності, в структурі різних механізмів багато загального. Тому для дослідження механізмів можна застосовувати загальні методи механіки. При кінематичному і силовому дослідженні машин і механізмів, як правило, створюючі їх елементи, можна вважати абсолютно твердими, оскільки переміщення від деформації тіл малі в порівнянні з переміщенням самих тіл.

Теорія машин і механізмів — це наукова дисципліна про загальні методи дослідження будови, кінематики і динаміки механізмів і машин та про наукові основи їх проектування. Рух механізмів залежить від їх будови і сил, що діють на них. Тому при викладенні теорії механізмів зручно проблеми аналізу механізмів розбити на три частини: 1) структурний аналіз; 2) кінематичний аналіз; 3) динамічний аналіз. У цьому зв'язку аналіз механізмів залежно від завдання може бути структурним, кінематичним і динамічним. Якщо при аналізі механізмів розміри їх ланок вважаються заданами й необхідно знайти ті чи інші кінематичні (переміщення, швидкості, прискорення) або силові (сили, моменти сил, роботу, потужність, ККД тощо) характеристики руху, то в процесі створення механізмів і машин виникає інша (зворотна) задача, а саме - побудувати такий механізм, який би відповідав необхідним функціональним або технологічним вимогам. Ці вимоги в кінцевому підсумку зводяться до виконання деяких геометричних або механічних умов. Така задача ТММ, зворотна до задачі аналізу, називається синтезом механізмів. Отже, під синтезом механізму розуміють проектування його схеми за заданими властивостями. При цьому розрізняють три основні етапи синтезу. Перший етап називають структурним синтезом який полягає у виборі структурної схеми механізму, що має потрібну кількість ступенів вільності, кількість та вид ланок і кінематичних пар, які забезпечують необхідні рухи ланок та їх взаємне розташування. Другий етап називається кінематичним синтезом, задача якого - визначити геометричні розміри ланок, що забезпечують задані кінематичні умови роботи механізму (положення ланок, траєкторії окремих точок, швидкості та прискорення ланок і точок механізму тощо). Якщо потрібно врахувати також динамічні властивості механізму, розв'язується більш загальна задача - динамічний синтез, під яким розуміють проектування кінематичної схеми механізму з визначенням параметрів, які характеризують розміри та розподіл мас ланок. Динамічний синтез містить у собі два попередні види синтезу.

В результаті вивчення даної дисципліни студент повинен уміти: визначати структуру і проводити аналіз механізмів; визначати кінематичні і динамічні характеристики механізмів; по вихідним кінематичним і динамічним параметрам технологічного процесу робочого механізму виконати аналіз будівельної машини в цілому, розрахувати її технічні і експлуатаційні характеристики; оптимізувати параметри проектованої машини (механізму) по завданим критеріям.

У розділі «Структура механізмів» викладені основні поняття і визначення, що стосуються даного розділу, наведені приклади розв'язання завдань щодо визначенню класу кінематичних пар, числа ступенів вільності механізмів і проведенню структурного аналізу механізмів. До кожної із запропонованих для аналізу схем механізмів дається коротке пояснення функціонального призначення механізму. Більшість контрольних завдань складена на прикладах механізмів і машин, що застосовуються в будівельній галузі.

I ОСНОВНІ ПОНЯТТЯ, ВИЗНАЧЕННЯ, ТЕРМІНОЛОГІЯ

1.1 Поняття механізму, види механізмів.

Механізм - система тіл, що призначена для перетворення руху одного або декількох твердих тіл в необхідні рухи інших твердих тіл. Механізми, що входять до складу машин, вельми різноманітні. Одні з них є поєднанням твердих тіл, інші можуть мати в своєму основному складі пружні, гнучкі ланки, гідравлічні, пневматичні, електричні або магнітні пристрої.

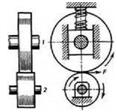
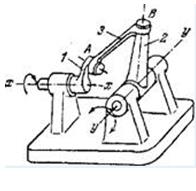
Згідно прийнятої конструктивно-функціональної класифікації механізми можна розділити на сім основних видів: важільні, кулачкові, фрикційні, зубчасті, з гнучкими ланками, гідравлічні, пневматичні. Приклади таких механізмів показані на рис.1.1,а,б,в,г і рис.1.2, д,е,ж, відповідно.

В важільних механізмах передача руху і зусилля від двигуна до виконавчого (робочого) органу здійснюється в основному за рахунок ланок, що є сукупністю стрижнів, сполучених між собою рухомими з'єднаннями.

а б

в г

Рис.1.1 Приклади механізмів: а-важільні; б- кулачкові;

в- фрікційні; г-зубчасті

д е

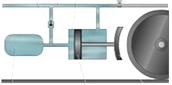
Резервуар Поршень Гальмівна колодка

Рис.1.2 Приклади механізмів: д- з гнучкими ланками; е- гідравлічні;

ж-пневматичні

Перевага кулачкових механізмів полягає в можливості здобуття практично будь-якого закону руху штовхача за рахунок відповідного вибору профілю кулачка. У фрикційних механізмах рух від вхідної ланки до вихідної передається за рахунок сил тертя, що виникають в місцях контакту ланок. До зубчастих механізмів відносяться механізми, до складу яких входять зубчасті передачі. Механізми з гнучкими зв'язками застосовують для передачі руху до робочого органу, який знаходиться на значній відстані від двигуна. Гідравлічний механізм – механізм, в якому перетворення руху від двигуна до робочого органу відбувається за допомогою твердих і рідких тіл. Пневматичний механізм – механізм, в якому перетворення руху від двигуна до робочого органу відбувається за допомогою твердих і газоподібних тіл.

1.2 Складові механізму

Будь-який механізм складається з окремих деталей, вузлів, складальних одиниць і кінематичних пар (рухомих з'єднань). Всі нерухомі деталі механізму утворюють одну жорстку нерухому систему тіл, що зветься нерухомою ланкою або стояком. Кожна рухома деталь або складальна одиниця механізму, що рухається в просторі як одне ціле, називається рухомою ланкою. Рухомі і нерухомі ланки сполучені між собою кінематичними парами так, що забезпечується можливість їх відносного руху (переміщення).

Розглянемо поняття і визначення, що характеризують будову механізмів.

1. Ланка механізму – тверде тіло, що входить до складу механізму, має елементи кінематичних пар і переміщується в просторі як єдине ціле.

2. Кінематична пара – рухоме з'єднання двох дотичних між собою ланок, що допускає їх відносний рух.

3. Елемент кінематичної пари – сукупність поверхонь, ліній і окремих точок однієї ланки, по яких він може стикатися з елементом іншої ланки, утворюючи кінематичну пару.

4. Стояк – ланка, що приймається за нерухому.

5. Вхідна ланка – ланка, якій надається рух, який перетворюється механізмом в необхідний рух іншої (вихідної) ланки. Вхідних ланок може бути декілька.

6. Вихідна ланка – ланка, що здійснює певний рух, для виконання якого призначений механізм. Вихідних ланок може бути декілька.

7. Початкова ланка – ланка, якій приписується одна або декілька узагальнених координат механізму.

8. Узагальнена координата механізму – незалежна координата початкової ланки, що визначає положення всіх останніх ланок механізму відносно стояка. У випадку якщо початкових ланок декілька, то кожна з незалежних між собою координат кожної початкової ланки визначає положення всіх останніх ланок механізму відносно стояка.

9. Число ступенів вільності механізму – число незалежних, можливих узагальнених координат механізму.

10. Кінематичний ланцюг – сукупність ланок, зв'язаних між собою кінематичними парами.

11. Замкнутий контур - сукупність послідовно сполучених ланок, в якому будь-яка з ланок сполучена з двома іншими ланками.

12. Замкнутий кінематичний ланцюг – кінематичний ланцюг, ланки якого утворюють один або декілька замкнутих контурів, кожна ланка якого входить в дві або більше кінематичні пари.

13. Незамкнутий кінематичний ланцюг – кінематичний ланцюг, ланки якого не утворюють замкнутих контурів і в якому є ланки, що входять лише в одну кінематичну пару.

14. Простий кінематичний ланцюг – кінематичний ланцюг, в якого кожна ланка входить не більше ніж в дві кінематичні пари.

15. Складний кінематичний ланцюг – кінематичний ланцюг, в якого є хоч би одна ланка, що входить більш ніж в дві кінематичні пари.

16. Кінематичне з'єднання – незамкнутий кінематичний ланцюг, що конструктивно замінює в механізмі певну кінематичну пару.

З урахуванням пункту 10 поняттю механізм можна дати декілька інше визначення. Механізм - це кінематичний ланцюг, до складу якого входить нерухома ланка (стояк), число ступенів вільності якого дорівнює числу узагальнених координат, що характеризують положення ланцюга відносно стояка.

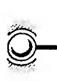
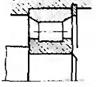
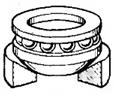
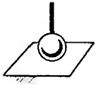
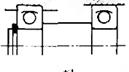
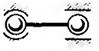
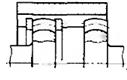
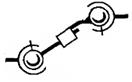
У таблиці 1.1 показані приклади кінематичних з'єднань і кінематичних пар (КП), які їх замінюють.

Таблиця 1.1. Кінематичні з'єднання і КП, які їх замінюють

Кінематичні з'єднання	КП , що їх замінюють	Кінематичні з'єднання	КП , що їх замінюють

2 КЛАСИФІКАЦІЯ КІНЕМАТИЧНИХ ПАР

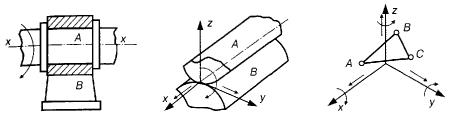
Кінематична пара є рухомим з'єднанням двох ланок, які стикаються. Можливі з'єднання ланок у кінематичні пари дуже різноманітні. Наприклад, на рис. 2.1,а зображено так звану однорухому обертову (обертальну) кінематичну пару, в якій ланки А і В з'єднані за допомогою двох циліндричних поверхонь. Бурти на тілі А (вала) обмежують відносний поступальний рух тіл А,В вздовж осі х — х, але не заважають їхньому відносному обертальному руху. На рис. 2.1,б зображено схему іншого способу сполучення елементів ланок А і В. Ця кінематична пара допускає відносне перекочування, ковзання і вертіння. Як відомо, у загальному випадку всяке абсолютно тверде тіло АВС (рис.2.1,в), що вільно рухається у просторі, має шість ступенів вільності.

а б в

Рис.2.1. Кінематичні пари: а- однорухома, обертальна; б-вища; в-тіло АВС, що вільно рухається у просторі

Рух такого тіла можна розглядати як обертання навколо осей х, у, z та поступальних рух вздовж цих самих осей. Таким чином, тіло АВС матиме шість видів незалежних можливих рухів: три обертальні і три поступальні.

На відносний рух кожної ланки кінематичної пари накладаються певні обмеження, які залежать від способу сполучення ланок кінематичної пари. Звісно, що ці обмеження називаються умовами зв'язку в кінематичних парах, а S число умов зв'язку, які накладає кінематична пара на відносний рух ланок. Таким чином, число умов зв'язку, накладених на відносний рух кожної ланки кінематичної пари, змінюється в межах від 1 до 5. Тоді число ступенів вільності Н ланки кінематичної пари у відносному русі може бути виражене рівнянням

H=6-S

Класифікація кінематичних пар здійснюється за такими ознаками:

1) числом умов зв'язку, які накладаються кінематичною парою на відносний рух ланок;

2) формою елементів ланок, що утворюють кінематичну пару;

3) за характером відносного руху ланок.

4) способом замикання пари.

Всі кінематичні пари (КП) підрозділяються на п'ять класів. Номер класу КП визначається числом умов зв'язку Ѕ, які накладені на рухи однієї ланки пари відносно іншої.

Ѕ=6-Н,

де Н - ступінь вільності.

Оскільки клас КП визначається кількістю накладених на відносний рух ланок обмежень, то кінематичні пари плоских і просторових механізмів відповідно до першої ознаки класифікуються як:

* однорухома пара 5-го класу – кінематична пара з одним ступенем вільності у відносному русі її ланок ;

* дворухома пара 4-го класу – кінематична пара з двома ступенями вільності у відносному русі її ланок;

* трьохрухома пара 3-го класу– кінематична пара з трьома ступенями вільностями у відносному русі її ланок;

* чотирьохрухома пара 2-го класу – кінематична пара з чотирма ступенями вільності у відносному русі її ланок;

* п'ятирухома пара 1-го класу – кінематична пара з п'ятьма ступенями вільності у відносному русі її ланок .

Отже кінематичні пари механізмів відповідно до першої ознаки можуть бути: а) 5-го класу ( S = 6-Н = 6-1=5 умов зв'язку), б) 4-го класу (S = 6-Н = 6-2=4 умови зв'язку), тощо, де Н ступінь вільності.

За другою ознакою КП можуть бути двох видів:

* нижчі КП, в яких контакт зв'язаних ланок, що стикаються при відносному русі, здійснюється по поверхні;

* вищі КП - в яких контакт зв'язаних ланок, що стикаються при відносному русі, здійснюється в точці або по лінії.

За третьою ознакою кінематичні пари 5-го класу можуть бути трьох видів: обертові (О), поступальні (П) і гвинтові (Г). Кінематичні пари 4-го класу є в зубчастих, кулачкових і інших механізмах. Для вирішення питання, до якого класу відноситься та або інша КП, слід поступати таким чином. Одну з ланок, що входять в КП уявити нерухомою і жорстко пов'язати з нею нерухому систему координат О_хуz, потім орієнтуючись по відношенню до нерухомої системи, встановити кількість зв'язків (неможливих відносних рухів) другої ланки .

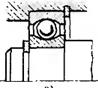
Число цих неможливих відносних рухів (число зв'язків) відповідає номеру класу КП. На прикладі сферичного шарніра (рис. 2.2) встановимо число зв'язків (неможливих відносних рухів) .

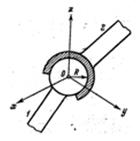
Рис.2.2 Сферична кінематична пара

Для цього жорстко пов'яжемо з ланкою 1 нерухому систему координат О_хyz. Ланка 2 не може здійснювати поступальний рух уздовж осей Ох, Оу, Оz, але обертатися відносно них може. Число умов зв'язку S=3, число ступенів вільності H=3. Це означає, що розглянута кінематична пара 3-го класу.

Якщо ж накласти ще умову площинності ( рух ланок лише в одній площині-плоский механізм), то виявиться, що ланка 2 зможе здійснювати обертальний рух навколо двох осей - перпендикулярній площині механізму і осі, що проходить через центр шарніра і вісь ланки 2. Для цього випадку S=4, H=2, пара 4-го класу. Якщо ланки 1,2 механізму можуть здійснювати лише плоскопаралельні рухи - зникає можливість обертання ланки 2 відносно своєї осі. В цьому випадку кінематична пара буде 5-го класу ( S=5, H=1).

За третьою ознакою КП можуть бути:

Нижчі пари – кінематичні пари, в яких необхідні відносні рухи ланок можуть бути отримані постійним стиканням їх елементів по поверхні.

Вищі пари – кінематичні пари, в яких необхідні відносні рухи ланок можуть бути отримані лише постійним стиканням їх елементів по лініях чи в точках контакту.

За четвертою ознакою КП можуть мати:

Силове замикання кінематичної пари – забезпечення контакту ланок пари за рахунок дії сил ваги, сили пружності пружини, тощо.

Геометричне замикання кінематичної пари – забезпечується за рахунок геометричної форми робочих поверхонь (елементів) і конструкції пари. Інші типи кінематичних пар, їх конструктивні схеми і умовні позначення на кресленнях наведені в таблиці. 2.1.

Таблиця 2.1 Конструктивні схеми і умовні позначення КП

№ п/п	Рисунок	Умовне позначення	Назва пари	Н	S	Клас пари
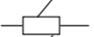
1			Обертова	1	5	V
2		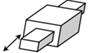	Поступаль- на	1	5	V
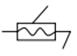
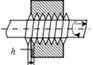
3			Гвинтова	1	5	V
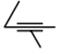
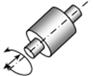
4			Циліндрич- на	2	4	IV
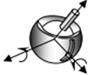
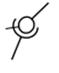
5			Сферична з пальцем	2	4	IV
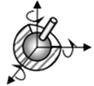
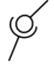
6			Сферична	3	3	III
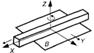
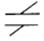
7			Площинна	3	3	III
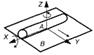
8			Циліндр - площина	4	2	II
9		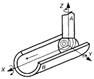	Куля - циліндр	4	2	II
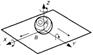
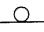
			Куля - площина	5	1	I

3 СТРУКТУРА МЕХАНІЗМІВ

3.1 Поняття про структуру механізму

1. Структурна схема механізму – схема механізму, що вказує на його будову, а саме: стояк; рухомі ланки; кінематичні пари, їх взаємне розташування і зв'язки.

2. Структурна формула кінематичного ланцюга – формула, що зв'язує кількість ступенів вільності (число його незалежних рухів) з кількістю і видом кінематичних пар в даному кінематичному ланцюгу.

3. Зайві ступені вільності – рухи деяких ланок механізму, що не роблять впливу на характер руху останніх ланок механізму.

4. Пасивні зв'язки – додаткові обмеження, що накладаються кінематичними парами на рух деяких ланок, але не надають вплив на характер руху всіх інших ланок механізму.

5. Замінюючий механізм – механізм, еквівалентний тому, що розглядається із заміною вищих пар нижчими.

3.2 Найменування деяких видів ланок

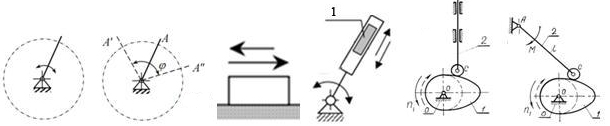
1. Кривошип – ланка важільного механізму, що обертається і здійснює повний оберт відносно нерухомої осі (рис. 3.1,а).

2. Коромисло – ланка важільного механізму, що обертається і може здійснювати лише неповний оберт φ відносно нерухомої осі (рис.3.1,б).

3. Шатун – ланка важільного механізму, що створює кінематичні пари лише з рухомими ланками (рис.3.2,б) і здійснює плоский рух.

4. Повзун – ланка важільного механізму, що утворює поступальну пару з іншою ланкою, зокрема із стояком (рис.3.1,в).

5. Куліса – ланка важільного механізму, що обертається відносно нерухомої осі і створює з іншою рухомою ланкою поступальну пару (рис.3.1,г).

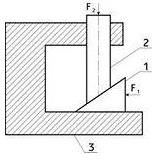
     6. Кулачок – ланка, що має елемент вищої кінематичної пари, виконаний у вигляді безперервної поверхні змінної кривизни -1 (рис.3.1,д,е).

     а            б                  в         г                  д                  е

Рис. 3.1 Види ланок: а-кривошип; б-коромисло, φ- кут хитання;

в-повзун; г-куліса, 1-кулісний камінь; д,е-кулачкові механізми

3.3 Найменування деяких видів механізмів

1. Плоский механізм - ланки якого здійснюють рухи в площині, паралельній одній і тій же нерухомій площині (рис.3.2, б).

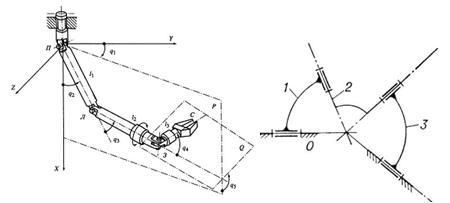
2. Просторовий механізм - в якого хоч би одна ланка здійснює просторовий рух (рис. 3.2, в, д).

3. Сферичний механізм – механізм, в якому всі постійні і миттєві осі обертання ланок перетинаються в одній точці (рис. 3.2, г).

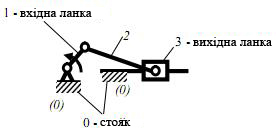
4. Важільний механізм – механізм, ланки якого утворюють лише обертові, поступальні, циліндричні і сферичні пари . Прикладами можуть

бути кривошипно-повзунний (рис. 3.2, а), кулісний (рис. 3.1, г), та просторовий механізм (рис. 3.2, д).

5. Шарнірний механізм – механізм, ланки якого утворюють лише обертові пари (рис. 3.2, ж, з, н).

6. Клиновий механізм – механізм, ланки якого утворюють лише поступальні пари (рис. 3.2, е)..

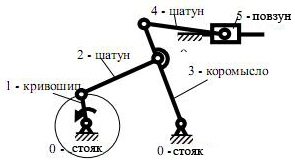
7. Шарнірний чотирьохланковик – шарнірний чотириланковий механізм (рис. 3.2, ж, з, и).

8. Кривошипно - коромисловий механізм – шарнірний чотириланковий, до складу якого входять кривошип і коромисло.

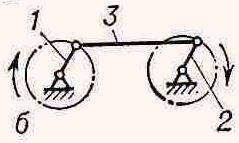
9. Двохкривошипний механізм – шарнірний чотирьохланковик, до складу якого входять два кривошипи (рис. 3.2, з).

10. Двохкоромисловий механізм – шарнірний чотирьохланковик, до складу якого входять два коромисла.

11. Кривошипно–повзунний механізм – важільний чотириланковий механізм, до складу якого входять кривошип і повзун (рис.3.2,а).

12. Коромислово–повзунний механізм – важільний чотириланковий механізм , до складу якого входять коромисло і повзун.

13. Кулісний механізм – важільний механізм , до складу якого входить куліса (рис. 3.2, к).

                         а                                                         б

в                                                      г



д                                       е                                    ж

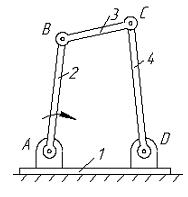
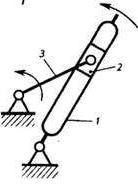
з                                            и                                к

Рис. 3.2 Приклади механізмів: а- кривошипно- повзунний; б- конвейєр, що коливається; в-просторовий маніпулятор; г-сферичний; д-шарнірний, просторовий; е-клиновий; д-шарнірний чотирьохланковик;

з- двохкривошипний; и- двохкоромисловий; к-кулісний

14. Кулачковий механізм – механізм, до складу якого входить кулачок (рис. 3.1, д, е).

Кулачкові механізми (рис.3.1,д,е) зазвичай призначені для перетворення обертального руху кулачка в зворотньо-поступальний рух вихідної ланки, якою, як правило, є штовхальник або коромисло 2.

15. Передавальний механізм – механізм для відтворення заданої функціональної залежності між переміщеннями ланок рушійного і виконуючого (робочого) механізму.

     16. Кроковий механізм – механізм, в якому вихідна ланка здійснює рух в одному напрямі з періодичними зупинками.

    17. Вистой – тривала зупинка вихідної ланки при безперервному русі вхідної ланки механізму.

               3.4 Структурні формули кінематичних ланцюгів

Раніше було встановлено, що коли на рух ланки у просторі не накладено ніяких умов зв'язку, то вона має шість ступенів вільності. Тоді якщо число ланок кінематичного ланцюга дорівнює к, то загальне число ступенів вільності, які мали к ланок до їхнього з'єднання у кінематичні пари, дорівнюватиме 6к. Кожна кінематична пара накладає різне число зв'язків на відносний рух ланок, що залежить від класу пари. Позначимо число пар І класу, що входять до складу ланцюга, через р₁,II — р₂, III — р₃, IV — р₄, V — р₅. Клас кінематичної пари визначається числом умов зв'язку, які накладає кожна кінематична пара на відносний рух ланок. Для визначення загального числа ступенів вільності ланок кінематичного ланцюга треба з 6к ступенів вільності, що їх ланки мали до того, як увійшли до кінематичної пари, вилучити ті ступені вільності, які віднімають кінематичні пари. Звісно, що одна пара І класу накладає на відносний рух ланок одну умову зв'язку (S = 1), II класу — дві (S = 2) і т. д. Тоді число ступенів вільності H, що їх має кінематичний ланцюг, становить

                                          H=6k-5p₅-4p₄-3p₃-2p₂-p₁(3.1)

Оскільки в механізмах одна ланка нерухома, то при вивченні руху всіх ланок механізму їхні абсолютні переміщення розглядаємо як такі, що відбуваються відносно однієї з ланок, прийнятої за нерухому. Якщо одна з ланок кінематичного ланцюга буде нерухомою, то загальне число ступенів вільності ланок ланцюга зменшиться на шість, тобто число ступенів вільності (рухомості) відносно нерухомої ланки

                                                W=H-6                                                   (3.2)

Підставляючи у (3.2) замість Н його вираз з (3.1), одержимо

                           W= 6(k-1)-5p₅-4p₄-3p₃-2p₂-p₁(3.3)

Якщо в (3.3) величину k-1 позначити n, то дістанимо

                          W= 6n-5p₅-4p₄-3p₃-2p₂-p₁(3.4)

де п — число рухомих ланок кінематичного ланцюга.

Формула (3.4) має назву формули рухомості або структурної формули кінематичного ланцюга загального вигляду.

Якщо механізм плоский, то на рух усіх ланок механізму в цілому накладено три загальні обмеження. Цю обставину треба взяти до уваги, підраховуючи ступені вільності окремих ланок і рухомості механізму в цілому. Якщо в загальному випадку число ступенів вільності рухомих ланок механізму дорівнює 6n, то для плоского механізму — (6 - 3)n = 3n, тобто тіло в плоскому русі має три ступеня вільності (два поступальні вздовж осей у і z,один обертовий навколо осі х). Відповідно з п'яти зв'язків, які накладає пара V класу, у цьому механізмі вона накладатиме тільки 5 - 3 = 2, оскільки три зв'язки вже накладено умовою паралельності осей пар і т. п. Тоді структурна формула механізму (3.4) перепишеться так:

                        W= (6-3)n-(5-3)p₅-(4-3)p₄-(3-3)p₃(3.5)

Тобто ступені вільності (рухомості) плоского механізму

                                   W= 3n-2p₅-p₄(3.6)

Це є структурна формула для плоских механізмів загального вигляду, або формула Чебишева.

В основу структурної класифікації механізмів покладено основний принцип їх утворення, який полягає в тому, що будь який механізм можна одержати шляхом приєднання до початкової ланки і стояка (механізму 1 класу) структурних груп, умовою існування яких є рівність:

для плоских механізмів

                                        W_гр = 3n-2p₅-p₄=0 ;                                           (3.7)

для просторових

                                         W_гр = 6n - 5p₅- 4p₄- 3p₃- 2p₂- p₁ = 0 ,             (3.8)

де W_гр- ступінь вільності групи, n-число рухомих ланок групи, р₁…..р₅- кількість кінематичних пар відповідного класу.

У сучасному машинобудуванні особливо широко поширені плоскі механізми, ланки яких входять до пар IV і V класів.

Механізм 1 класу – початкова ланка, що з'єднана кінематичною парою V класу із стояком.

Група Ассура – незамкнутий кінематичний ланцюг з нульовим ступенем вільності.

Замкнутий контур - сукупність ланок і кінематичних пар, що створюють замкнутий контур, який переміщується в просторі як єдине ціле.

Клас контура – визначається числом кінематичних пар, в які входять ланки, що утворюють контур.

Клас групи Ассура – визначається найвищим класом контура, що входить до складу групи.

Базисна ланка – ланка, що входить в три кінематичні пари і створює жорсткий контур.

Порядок групи Ассура – число елементів кінематичних пар, якими група приєднується до основного механізму.

Двохповодкова група ланок – група 2-го класу 2-го порядку, що має дві ланки і три кінематичні пари 5-го класу.

4 ЗАЙВІ СТУПЕНІ ВІЛЬНОСТІ Й УМОВИ ЗВ'ЯЗКУ

Під час дослідження структури механізмів можуть виявитися ступені вільності та умови зв'язку, що не впливають на рухомість механізму в цілому. Такі ступені вільності і умови зв'язку називають зайвими. Як приклад, на рис. 4.1 зображено схему кулачкового механізму, до складу якого входить стояк 0, кулачок 1 штовхач 2, ролик 3. Стояк і кулачок утворюють обертову пару V класу, кулачок і ролик — пару IV класу, штовхач і стояк — поступальну пару V класу, штовхач і ролик — обертову пару V класу. Тоді, виходячи з числа рухомих ланок і кінематичних пар, ступінь вільності механізму за формулою Чебишова

                                        W = 3n-2p₅-p₄=3×3-2×3-1=2

Прот

⇐ Предыдущая 1 2 3 4 56