Методичні вказівки 3 страница

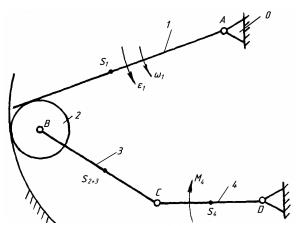
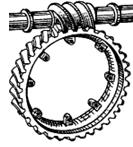
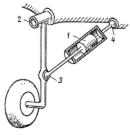
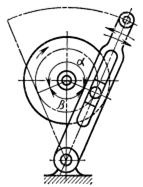
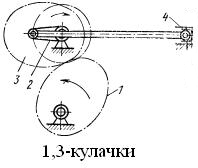
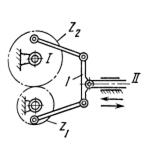
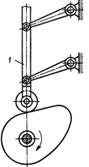
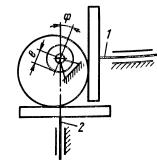
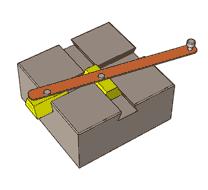
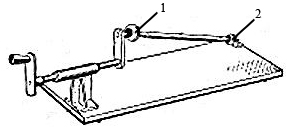
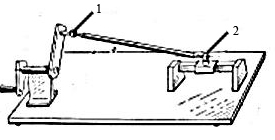
Рис.7.5. Схема кінематичного ланцюга з роликом, що обертається

Таблиця 7.4. Характеристика кінематичних пар

Позначення КП	А	В'	В	В"	С	D
Ланки, що створють кінемат. пари	0-1	1-2	2-3	2-0	4-3	4-0
Вид руху, що допускається	оберт.	оберт. поступ.	оберт.	оберт. поступ.	оберт.	оберт.
Хар-ка кінемат. пари	нижча	вища	нижча	вища	нижча	нижча
Клас КП	5	4	5	4	5	5

Визначемо ступінь вільності по формулі Чебишева для плоского ланцюга:

W = 3n-2P_н -P_в =3×4-2×4-2 = 2,

де: n = 4 - число рухомих ланок;

Р_н =4 - число нижчих кінематичних пар;

Р_в = 2 - число вищих кінематичних пар.

Отримана ступінь вільності W = 2. Неважко переконатися, що ролик 2 створює зайвий ступінь вільності оскільки обертання ролика не впливає на рухомість механізму. Відзначаємо, що в механізму ступінь вільності і число узагальнених координат мають бути рівні. Отож є зайва ступінь вільності - обертання ролика. Закріпимо ролик і визначимо ступінь вільності кінематичного ланцюга (табл.7.5, структурна схема рис.7.б).

Таблиця 7.5. Характеристика кінематичних пар

Позначення КП	А	В'	В"	С	D
Ланки, що створюють кінемат. пари	0-1	1-3	3-0	4-3	4-0
Вид руху, що допускається	оберт.	оберт. поступ.	оберт. поступ.	оберт.	оберт.
Хар-ка кінемат. пари	нижча	вища	вища	нижча	нижча
Клас КП	5	4	4	5	5

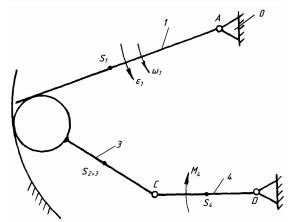
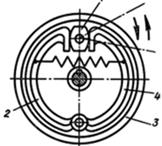
Рис. 7.6. Схема кінематичного ланцюга із закріпленим роликом

В цьому випадку кількість ланок і нижчих кінематичних пар зменшилася на одиницю. Визначимо ступінь рухомості для механізму на рис.7.6.

W = 3n-2P_н -P_в=3×3-2×3-2 = 1.

Даний кінематичний ланцюг є механізмом з вищими кінематичними парами. Замінимо вищі пари двома ланками, що мають чотири нижчі (3-обертальні і одну поступальну) кінематичні пари. Отримана ланка 2 є шатуном, а ланка 5 - коромислом (структурна схема рис.7.7.). Ланки кінематичного ланцюга мають ті ж назви, лише замість ролика 2 ланка 2 буде шатуном, а 5 - коромислом. В даному ланцюзі стало 7 нижчих кінематичних пар (таблиця.7.6.).

Даний кінематичний ланцюг є механізмом, оскільки ступінь вільности збігається з числом заданих рухів.

W=3n-2p₅=3× 5-2× 7=1

Таблиця 7.6. Характеристика кінематичних пар

Позначення	А	В'	В	В"	С	D	Е
Ланки, що створють кінемат. пари	0- 1	1 -2	2-5	2-3	4-3	4-0	5-0
Вид руху, що допускається	оберт.	поступ.	оберт.	оберт.	оберт.	оберт.	оберт.
Хар-ка кінемат. пари	нижча	нижча	нижча	нижча	нижча	нижча	нижча
Клас КП	5	5	5	5	5	5	5

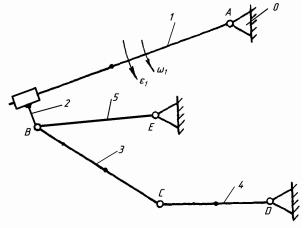
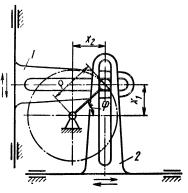
Рис.7.7. Схема механізму після заміни вищих пар нижчими

Визначимо клас механізму: Виділяємо структурні групи, починаючи з ланки, найбільш віддаленої від початкової. Структурна група 4-3 (рис. 7.8).

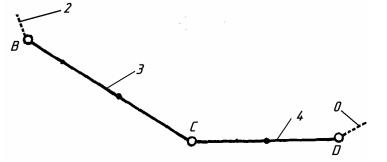
Рис.7.8 .Схема структурної групи

Ступінь рухомості:

W = 3n-2р₅ —р₄ = 3×2-2×3-0 = 0.

Клас 2. Порядок 2. Вид 1.

Структурна група 2-5 ( рис. 7.9.):

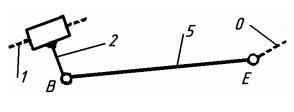
Рис.7.9.

Ступінь вільності:

W = 3n-2р₅-р₄ =3×2-2×3-0 = 0.

Клас 2. Порядок 2. Вид 2.

Механізм I класу з початковою ланкою (рис. 7.10).

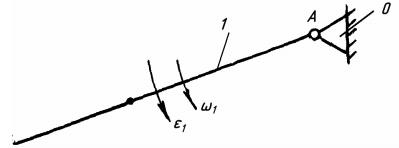
Рис. 7.10

Ступінь вільності:

W = 3n-2р₅-р₄ = 3×1 -2×1-0 = 1 .

Даний механізм 2-го класу, тому що структурні групи, що входять до його складу, 2-го класу.

Приклад 5.4.

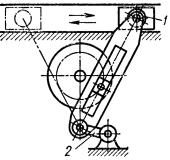
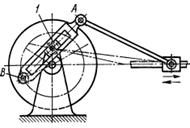
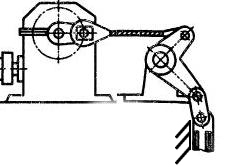
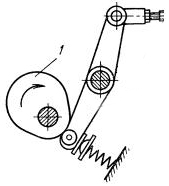
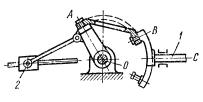
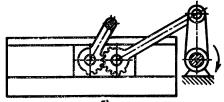
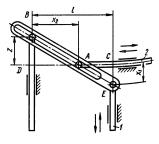
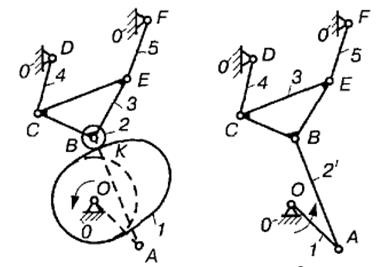
Виконати структурний аналіз кулачково-важільного механізму, схему якого зображено на рис. 7.11, а. Початковою ланкою вибрати кулачок 1.

Розв'язання. Механізм складається з п'яти рухомих ланок (n =5), шести кінематичних пар V класу (р₅ = 6), а саме 0(0,1), В(2,3), С(3,4), D(4, 0), Е(3, 5),

F(5,0) і одної пари IV класу (р₄ = 1) К(1,2).Якщо підрахувати число ступенів вільності за цими даними, одержимо

W= 3n - 2р₅ - р₄= 3 × 5 - 2 × 6 - 1 = 2.

а б

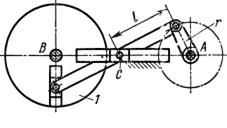
Рис. 7.11.Механізм: а-початкова схема; б-схема після заміни вищої пари

Тут ролик 2 створює зайвий ступінь вільності (обертання ролика відносно своєї осі). Будуємо замінний механізм відкинувши ролик. Для цього вищу пару К (пару IV класу) замінюємо нижчими парами V класу. Центр кривизни ролика 2 знаходиться у точці В, ацентр кривизни профілю кулачка 1 в точці контакту - у точці А. У точках А і В розміщуємо центри шарнірів додаткової умовної ланки 2' (рис. 7.11, б), які з'єднуємо з кулачком 1 (ланка ОА) і ланкою 3.

У замінному механізмі маємо n= 5, р₅= 7, р₄ = 0, тоді

W= 3n - 2р₅-р₄ = 3 × 5- 2 × 7 - 0 = 1.

Отже, у такому механізмі потрібна лише одна початкова ланка. Залишимо такою ланкою кулачок 7 (на рис. 7.11, б — кривошип ОА), який разом зі стояком О утворює механізм І класу.

Кінематичний ланцюг, що залишається після відокремлення механізму І класу, не можна розкласти на групи II класу. Ланки 2', 3, 4, 5 утворюють групу III класу III порядку, причому ланка 3є базисною, тому механізм, схему якого зображено на рис. 5. 11, а, треба віднести до III класу. Формула будови такого механізму має вигляд

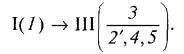
ЛІТЕРАТУРА, ЩО РЕКОМЕНДУЄТЬСЯ

1.Артоболевский И.И. Теория механизмов и машин.-М.,"Наука", 1988.- 638 с.

2. Фролов К.В. и др. Теория механизмов и машин. -М., "Высшая школа", 1987.-496 с.

3. Кожевников С.Н. Теория механизмов и машин.-М., "Наука", 1973.-502 с.

4. Колчин Н.И., Мовнин М.С. Теория механизмов и машин. -Л., "Судпромгиз", 1962.-616 с.

5. Заблонский К.И. и др. Теория механизмов и машин. -К., "Вища школа", 1989. -375 с.

6.Кіницький Я.Т. Теорія механізмів і машин.-К.,"Наукова думка", 2002. - 650 с.

7. А.Ф. Крайнев. Словарь-справочник по механизмам.-М., "Машиностроение", 1981.-438 с.

Контрольна робота № 1.

1. Вказати, які ступені вільності і їх кількість мають ланки в їх відносному русі.

2. Вказати, які умови зв'язку і їх кількість мають ланки у відносному русі.

3. Визначити клас кінематичної пари, утвореної ланками, що стикаються.

4. Вказати форму елементів кінематичної пари, що її утворюють.

5. Вказати вид кінематичної пари /вища або нижча/.

6. Вказати спосіб замикання ланок в кінематичній парі.

7. Накреслити умовне зображення кінематичної пари.

Приклад.

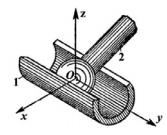
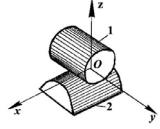
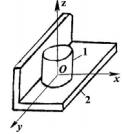
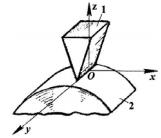
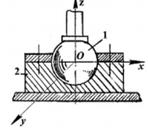
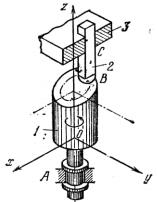
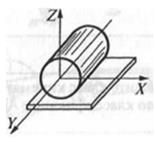
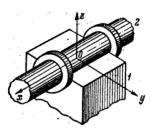
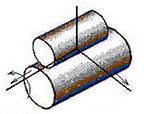
Дано зображення кінематичної пари на рис.1.

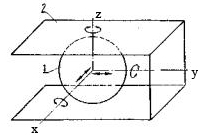
Рис.1 Зображення кінематичної пари

Розв'язання.

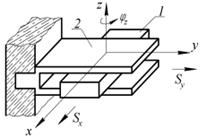
1. Для визначення ступенів вільності ланок 1,2 у відносному русі, другу ланку жорстко пов'яжемо з нерухомою системою координат х,у,z. Тоді ланка 1 матиме п'ять ступенів вільності (5-ть незалежних рухів) відносно нерухомої ланки 2, а саме: φ_х; φ_у; φ_z; s_x; s_y (3 обертальні і 2 поступальні рухомості, тобто Н=5).

2. Число умов зв'язку дорівнює одиниці (s=1), а саме S_z.

3. Оскільки клас кінематичної пари визначається числом зв'язків, накладених на відносний рух дотичних ланок, то підрахуємо їх кількість.

S = 6 - H = 6 - 5 = 1

4. Форма елементів ланок, що утворюють кінематичну пару - точка.

5. Вид кінематичної пари - вища.

6. Спосіб замикання ланок - геометричний, тому що ланка 2 обмежує відносний рух ланки 1 за рахунок своєї конструктивної форми.

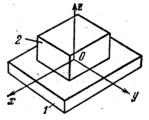
7. Умовне зображення кінематичної пари має вигляд (рис.2).

______

Рис.2. Умовне зображення кінематичної пари

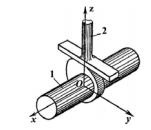
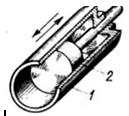
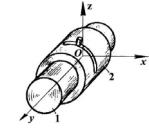
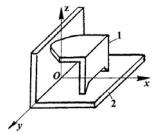
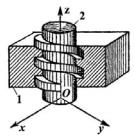
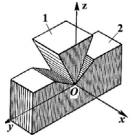
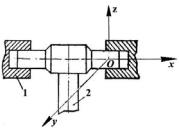
Зображення кінематичних пар

1
		5
7

				15
			18


			27
28	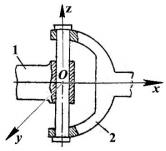29		30

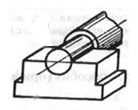
	32
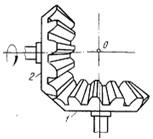
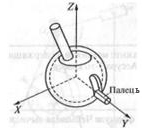
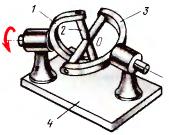
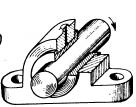
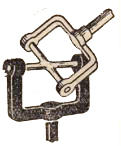		Карданий шарнир
	38	39
40

	47

52	53

Контрольна робота №2

1. Накреслити структурну схему механізму за допомогою умовних зображень.

2. Підрахувати число рухомих ланок механізму.

3. Визначити кількість кінематичних пар кожного класу.

4. Визначити ступінь вільності механізму.

Приклад 1.

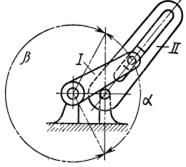
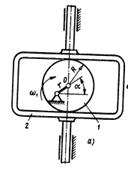
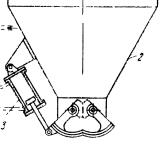
Дана принципова схема механізму на рис.1

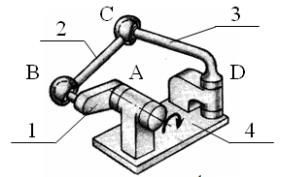
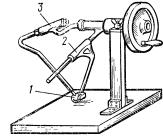
Рис.1 Принципова схема механізму

Розв'язання.

1. Структурна схема механізму в умовних зображеннях має вигляд

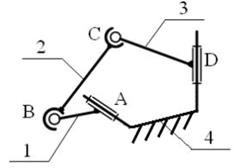
Рис.2. Схема механізму в умовних зображеннях

2. Рухомі ланки 1, 2, 3 пронумеровані і показані на рис.2, а їх кількість дорівнює трьом.

3. Кількість кінематичних пар :

5-го класу-дві: А(4,1); D(3,4).

4-го класу- немає;

3-го класу-дві: B(1,2); C(2,3).

2-го класу- немає;

1-го класу- немає.

4. Ступінь вільності просторового механізму визначається відомим співвідношенням

W=6n-5p₅-4p₄-3p₃-2p₂-p₁=6×3-5×2-4×0-3×2-2×0-0=2

Приклад 2.

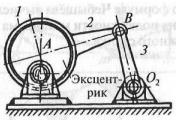
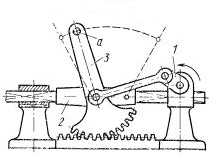
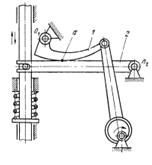
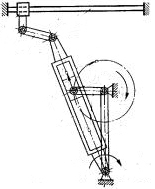
Дана принципова схема механізму на рис.3

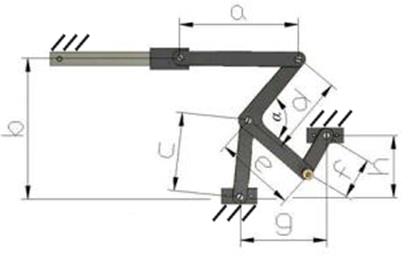
Рис.3 Принципова схема механізму

Розв'язання.

1. Структурна схема механізму в умовних зображеннях має вигляд (рис.4)

2. Ланки 1, 2, 3,4,5,6 пронумеровані і показані на рис.4. Кількість рухомих ланок n=5.

Нерухома ланка (стояк) позначена номером 6.

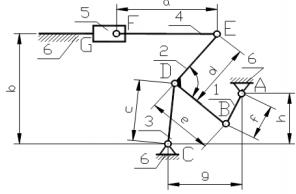
Рис.4. Схема механізму в умовних зображеннях

3. Кількість кінематичних пар :

5-го класу-сім: G(6,5); F(5,4);E(4,2);D(2,3);B(1,2);A(6,1);C(6,3).

4-го класу- немає;

3-го класу- немає;

2-го класу- немає;

1-го класу- немає.

4. Всі точки ланок описують траєкторії, що лежать в одній або паралельних площинах, тому ступінь вільності плоского механізму визначається за формулою Чебишева

W=3n-2p₅-p₄=3×5 - 2×7- 0 =1

Приклад 3.

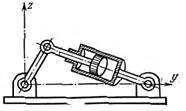
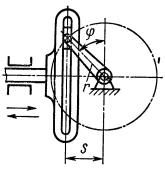
Дана принципова схема механізму на рис.5.

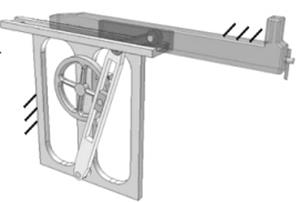
Рис.5 Принципова схема механізму

Розв'язання.

1. Структурна схема механізму в умовних зображеннях має вигляд (рис.6)

2. Ланки 1, 2, 3,4,5,6 пронумеровані і показані на рис.6. Кількість рухомих ланок n=5. Нерухома ланка (стояк) позначена номером 6.

3. Кількість кінематичних пар :

5-го класу-сім: F(5,6);G(5,4);E(4,3);B(1,2);C(2,3);A(1,6);D(3,6).

4-го класу- немає;

3-го класу- немає;

2-го класу- немає;

1-го класу- немає.

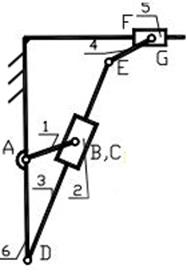
Рис.6 Схема механізму в умовних зображеннях

4. Ступінь вільності плоского механізму визначається відомим співвідношенням

W=3n-2p₅-p₄= 3×5 - 2×7- 0 =1

Варіанти схем механізмів

1


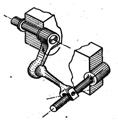
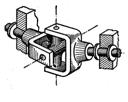
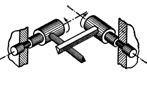
10	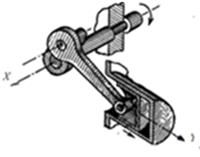		12 3-сферичний шарнир
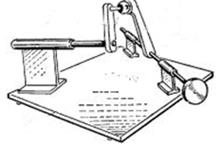4-сферичний шарнир			1-сферичний шарнир





			33
	35		36


43			45
46

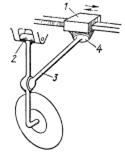3,4-сферичний шарнир
1,2-сферичні шарніри		1,2-сферичні шарніри

⇐ Предыдущая 1 2 345 6 Следующая ⇒