Методичні вказівки 2 страница

5. Шарнірний механізм – механізм, ланки якого утворюють лише обертові пари (рис. 3.2, ж, з, н).

6. Клиновий механізм – механізм, ланки якого утворюють лише поступальні пари (рис. 3.2, е)..

7. Шарнірний чотирьохланковик – шарнірний чотириланковий механізм (рис. 3.2, ж, з, и).

8. Кривошипно - коромисловий механізм – шарнірний чотириланковий, до складу якого входять кривошип і коромисло.

9. Двохкривошипний механізм – шарнірний чотирьохланковик, до складу якого входять два кривошипи (рис. 3.2, з).

10. Двохкоромисловий механізм – шарнірний чотирьохланковик, до складу якого входять два коромисла.

11. Кривошипно–повзунний механізм – важільний чотириланковий механізм, до складу якого входять кривошип і повзун (рис.3.2,а).

12. Коромислово–повзунний механізм – важільний чотириланковий механізм , до складу якого входять коромисло і повзун.

13. Кулісний механізм – важільний механізм , до складу якого входить куліса (рис. 3.2, к).

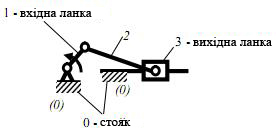
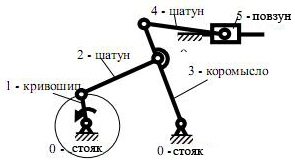
а б

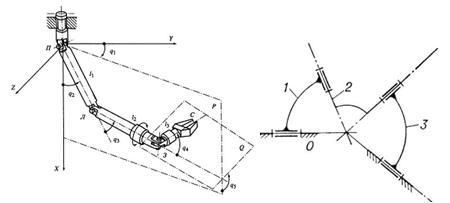
в г

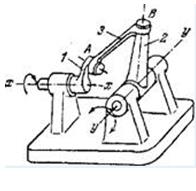
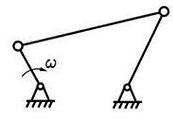
д е ж

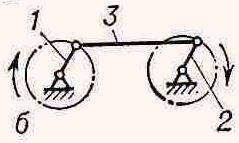
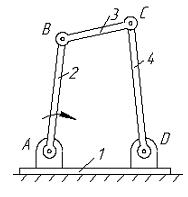
з и к

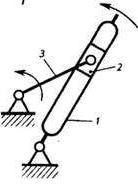
Рис. 3.2 Приклади механізмів: а- кривошипно- повзунний; б- конвейєр, що коливається; в-просторовий маніпулятор; г-сферичний; д-шарнірний, просторовий; е-клиновий; д-шарнірний чотирьохланковик;

з- двохкривошипний; и- двохкоромисловий; к-кулісний

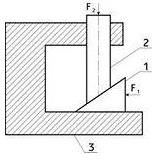
14. Кулачковий механізм – механізм, до складу якого входить кулачок (рис. 3.1, д, е).

Кулачкові механізми (рис.3.1,д,е) зазвичай призначені для перетворення обертального руху кулачка в зворотньо-поступальний рух вихідної ланки, якою, як правило, є штовхальник або коромисло 2.

15. Передавальний механізм – механізм для відтворення заданої функціональної залежності між переміщеннями ланок рушійного і виконуючого (робочого) механізму.

16. Кроковий механізм – механізм, в якому вихідна ланка здійснює рух в одному напрямі з періодичними зупинками.

17. Вистой – тривала зупинка вихідної ланки при безперервному русі вхідної ланки механізму.

3.4 Структурні формули кінематичних ланцюгів

Раніше було встановлено, що коли на рух ланки у просторі не накладено ніяких умов зв'язку, то вона має шість ступенів вільності. Тоді якщо число ланок кінематичного ланцюга дорівнює к, то загальне число ступенів вільності, які мали к ланок до їхнього з'єднання у кінематичні пари, дорівнюватиме 6к. Кожна кінематична пара накладає різне число зв'язків на відносний рух ланок, що залежить від класу пари. Позначимо число пар І класу, що входять до складу ланцюга, через р₁,II — р₂, III — р₃, IV — р₄, V — р₅. Клас кінематичної пари визначається числом умов зв'язку, які накладає кожна кінематична пара на відносний рух ланок. Для визначення загального числа ступенів вільності ланок кінематичного ланцюга треба з 6к ступенів вільності, що їх ланки мали до того, як увійшли до кінематичної пари, вилучити ті ступені вільності, які віднімають кінематичні пари. Звісно, що одна пара І класу накладає на відносний рух ланок одну умову зв'язку (S = 1), II класу — дві (S = 2) і т. д. Тоді число ступенів вільності H, що їх має кінематичний ланцюг, становить

H=6k-5p₅-4p₄-3p₃-2p₂-p₁(3.1)

Оскільки в механізмах одна ланка нерухома, то при вивченні руху всіх ланок механізму їхні абсолютні переміщення розглядаємо як такі, що відбуваються відносно однієї з ланок, прийнятої за нерухому. Якщо одна з ланок кінематичного ланцюга буде нерухомою, то загальне число ступенів вільності ланок ланцюга зменшиться на шість, тобто число ступенів вільності (рухомості) відносно нерухомої ланки

W=H-6 (3.2)

Підставляючи у (3.2) замість Н його вираз з (3.1), одержимо

W= 6(k-1)-5p₅-4p₄-3p₃-2p₂-p₁(3.3)

Якщо в (3.3) величину k-1 позначити n, то дістанимо

W= 6n-5p₅-4p₄-3p₃-2p₂-p₁(3.4)

де п — число рухомих ланок кінематичного ланцюга.

Формула (3.4) має назву формули рухомості або структурної формули кінематичного ланцюга загального вигляду.

Якщо механізм плоский, то на рух усіх ланок механізму в цілому накладено три загальні обмеження. Цю обставину треба взяти до уваги, підраховуючи ступені вільності окремих ланок і рухомості механізму в цілому. Якщо в загальному випадку число ступенів вільності рухомих ланок механізму дорівнює 6n, то для плоского механізму — (6 - 3)n = 3n, тобто тіло в плоскому русі має три ступеня вільності (два поступальні вздовж осей у і z,один обертовий навколо осі х). Відповідно з п'яти зв'язків, які накладає пара V класу, у цьому механізмі вона накладатиме тільки 5 - 3 = 2, оскільки три зв'язки вже накладено умовою паралельності осей пар і т. п. Тоді структурна формула механізму (3.4) перепишеться так:

W= (6-3)n-(5-3)p₅-(4-3)p₄-(3-3)p₃(3.5)

Тобто ступені вільності (рухомості) плоского механізму

W= 3n-2p₅-p₄(3.6)

Це є структурна формула для плоских механізмів загального вигляду, або формула Чебишева.

В основу структурної класифікації механізмів покладено основний принцип їх утворення, який полягає в тому, що будь який механізм можна одержати шляхом приєднання до початкової ланки і стояка (механізму 1 класу) структурних груп, умовою існування яких є рівність:

для плоских механізмів

W_гр = 3n-2p₅-p₄=0 ; (3.7)

для просторових

W_гр = 6n - 5p₅- 4p₄- 3p₃- 2p₂- p₁ = 0 , (3.8)

де W_гр- ступінь вільності групи, n-число рухомих ланок групи, р₁…..р₅- кількість кінематичних пар відповідного класу.

У сучасному машинобудуванні особливо широко поширені плоскі механізми, ланки яких входять до пар IV і V класів.

Механізм 1 класу – початкова ланка, що з'єднана кінематичною парою V класу із стояком.

Група Ассура – незамкнутий кінематичний ланцюг з нульовим ступенем вільності.

Замкнутий контур - сукупність ланок і кінематичних пар, що створюють замкнутий контур, який переміщується в просторі як єдине ціле.

Клас контура – визначається числом кінематичних пар, в які входять ланки, що утворюють контур.

Клас групи Ассура – визначається найвищим класом контура, що входить до складу групи.

Базисна ланка – ланка, що входить в три кінематичні пари і створює жорсткий контур.

Порядок групи Ассура – число елементів кінематичних пар, якими група приєднується до основного механізму.

Двохповодкова група ланок – група 2-го класу 2-го порядку, що має дві ланки і три кінематичні пари 5-го класу.

4 ЗАЙВІ СТУПЕНІ ВІЛЬНОСТІ Й УМОВИ ЗВ'ЯЗКУ

Під час дослідження структури механізмів можуть виявитися ступені вільності та умови зв'язку, що не впливають на рухомість механізму в цілому. Такі ступені вільності і умови зв'язку називають зайвими. Як приклад, на рис. 4.1 зображено схему кулачкового механізму, до складу якого входить стояк 0, кулачок 1 штовхач 2, ролик 3. Стояк і кулачок утворюють обертову пару V класу, кулачок і ролик — пару IV класу, штовхач і стояк — поступальну пару V класу, штовхач і ролик — обертову пару V класу. Тоді, виходячи з числа рухомих ланок і кінематичних пар, ступінь вільності механізму за формулою Чебишова

W = 3n-2p₅-p₄=3×3-2×3-1=2

Проте очевидно, що у цьому механізмі досить знати положення одного кулачка, щоб однозначно визначити положення штовхача, тобто досить мати одну початкову ланку, а не дві, як це випливає з формули Чебишова. В цьому механізмі ролик З створює зайвий ступінь вільності, він може перекочуватися і ковзати відносно кулачка, що не впливає на характер руху штовхача. Ролик є конструктивним елементом, який введено для заміни тертя ковзання тертям кочення, тобто для зменшення опору сил тертя і зношення ланок. Кінематика механізму не змінюється, якщо ролик забрати і штовхач 2 безпосередньо з'єднати з кулачком 1 у кінематичну пару IV класу (на рис. 4.1 цей випадок показано штриховою лінією).

На рис. 4.2 зображено механізм спарника (паралельних кривошипів), з розмірами ланок: АВ= СD, АD= ЕF= ВС, АЕ= DFі BE=CF. За кількістю рухомих ланок (п = 4) і пар V класу (р₅ = 6) ступінь вільності механізму W= 0, тобто цей кінематичний ланцюг є нерухомою фермою. Проте, коли ланка EF паралельна ланці ВС, механізм мас один ступінь вільності (W = 1), оскільки фігура АВСD завжди утворює паралелограм, і, отже, відстань між точками Е і F ніколи не змінюється і дорівнює відстані між точками А і D або В і С. Тоді без усякого порушення характеру руху механізму ланку ЕF (або ВС) можна забрати, оскільки ця ланка накладає на рух механізму зайві (пасивні) зв'язки, тобто нові зв'язки на вже існуючі.

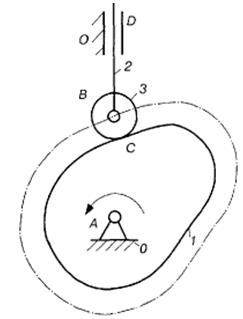
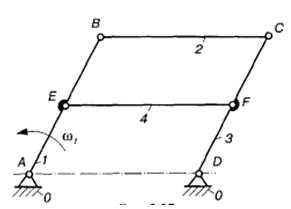
Рис.4.1 Кулачковий Рис.4.2 Механізм паралелограма

механізм з пасивним зв'язком

На практиці вводять ланку ЕF для збільшення жорсткості механізму.

Під час проведення структурного аналізу механізму необхідно позбутися зайвих ступенів вільності і пасивних зв'язків.

5 ЗАМІНА ВИЩИХ КІНЕМАТИЧНИХ ПАР НИЖЧИМИ

При структурному аналізі механізмів вищі кінематичні пари зручно замінити нижчими. При цьому має задовольнятися умова структурної еквівалентності, тобто щоб замінний механізм мав таке саме число ступенів вільності і щоб характер миттєвого відносного руху не змінився. На рис.5.1,а І зображено схему три-ланкового плоского механізму з двома обертовими парами (А і В)та однією вищою парою С, утвореною ланками 1, 2. Профілями елементів пари С є дві дуги кіл з центрами К₁ і К₂. Ступінь вільності такого механізму

W = 3n-2p₅-p₄=3×2-2×2-1=1 (5.1)

Незважаючи на те що точка С дотику профілів ланок 1, 2 під час руху механізму змінює своє положення, відстань К₁ К₂ = г₁ + г₂ = соnst. Тому заданий механізм буде еквівалентний плоскому шарнірному чотириланковому механізму (рис. 5.1, б), в якого довжини відрізків АК₁, К₁К₂, ВК₂ такі самі, як на рис. 5.1, а, і ступінь вільності

W = 3n-2p₅-p₄=3×3-2×4-0=1 (5.2)

Замінний механізм АК₁К₂В еквівалентний заданому і за законом руху ланок, тобто зберігається відношення швидкостей ω₁/ ω_{1 .}

Порівнюючи механізми, зображені на рис. 5.1, а, б, та залежності (5.1) і (5.2), бачимо, що вища пара у плоских механізмах еквівалентна одній умовній ланці і двом кінематичним парам V класу.

Розглянутий спосіб заміни механізму можна узагальнити й тоді, коли профілями вищих пар є криві змінної кривизни і мають спільну дотичну в точках спряження профілів (рис. 5.1, в). Однак у цьому випадку кожному положенню механізму відповідають різні еквівалентні "миттєві" шарнірні чотириланкові механізми АК₁К₂В, у яких К₁ і К₂ є миттєвими центрами кривизни профілів, що відповідають точці С дотику.

Таким чином, щоб замінити вищу кінематичну пару нижчою, необхідно ввести додатково умовну ланку з двома обертовими кінематичними парами V класу, центри шарнірів яких треба розмістити у центрах кривизни профілів ланок, що утворюють цю вищу пару, і заново введену ланку слід з'єднати нижчими парами з тими ланками, які входили до складу вищої пари.

На рис. 5.2 показано інші приклали побудови замінних механізмів (а, в, д, є — дійсні механізми; б, г, е, ж — відповідні їм замінні механізми). Якщо профілем будь-якої ланки вищої кінематичної пари є пряма, то обертова пара переходить у поступальну (центр кривизни такого профілю знаходиться у нескінченності).

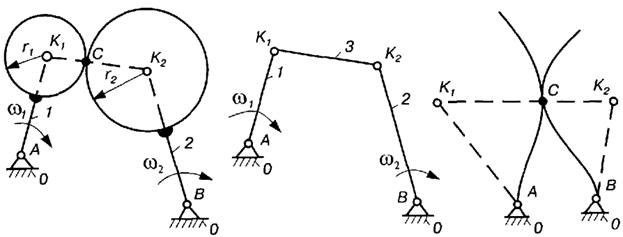
а б в

Рис.5.1

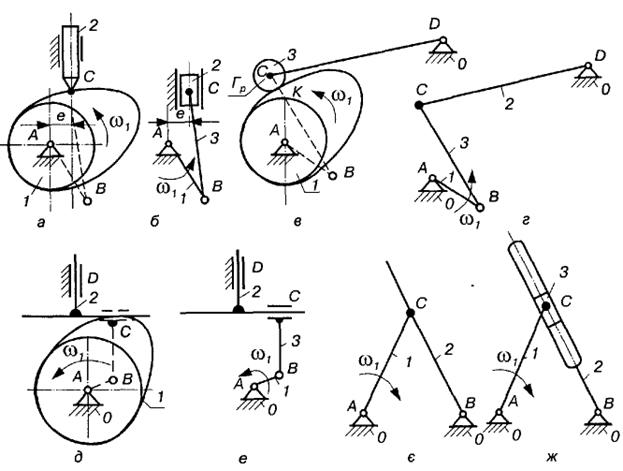
Рис.5.2

6 ПРИКЛАДИ ВИЗНАЧЕННЯ СТУПЕНІВ ВІЛЬНОСТІ МЕХАНІЗМУ

При розв'язанні завдань по даній темі спочатку необхідно встановити технологічне призначення механізму, встановити тип механізму (плоский або просторовий) і потім визначити число ступенів вільності.

Приклад 6.1. Визначити число ступенів вільності W механізму в'язальної машини (рис.6.1) для прошивки мішкоподібної тари, що використовувається для упаковки сипких і пилоподібних будівельних сумішей.

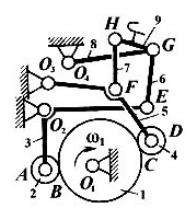
Рис. 6.1 Структурна схема в'язальної машини

Розв'язання. Призначення даного механізму: надати гачку, що розташований на шатуні 9, петлеподібний рух. Рух гачку надається від кулачка 1 через коромисла 3, 5 і шатуни 6, 7. У механізмі 9 рухомих ланок: кулачок 1, ролики 2, 4, коромисла 3, 5, 8, шатуни 6, 7, 9. Кінематичних пар V класу 11: О₁(створена ланками 0 і 1); О₂(0,3); О₃(О,5); О₄(О,8); А(2,3); D(4,5); Е(3,6); F(5,7); G₁(8,9); С₂(8,6); H(7,9). Кінематичних пар IV класу 2: В(1,2), С(1,4). Кінематичних пар інших класів в механізму немає, оскільки всі ланки виконують рух в паралельних плоскостях, тобто механізм є плоским. Тоді за формулою Чебишева для плоских механізмів визначаємо W.

W= 3x9-2x11-2 = 3

Приклад 4.2. Визначити число ступенів вільності механізму пантографа підвісного маніпулятора (рис.4.2).

Розв'язання. Механізм призначений для копіювання в масштабі рухів привідних пристроїв, передачі руху і для поступального орієнтування вихідної ланки. Спільний рух ланок 2, 4, 5 дозволяє переміщувати схват 13 в площині і обертати вісь LN.

В механізмі 13 рухомих ланок: 1,2, 3, 4,5,6, 7,8, 9, 10, 11, 12, 13. Кінематичних пар V-го классу 17: А (1, 2); В₁ (1, 5), В₂(1, 4), С (2, 3), D(0,1), G₁ (5, 7), G₂(5, 8), I (4, 6), H(6, 7), F(7, 9), J₁(3, 8), J₂ (8, 10), E(9, 10), K (10. 11), L(11, 12), М(9, 12), N(12, 13).

За формулою Чебишева для плоских механизмів визначаєм W.

W = 3x12-2x16 = 4.

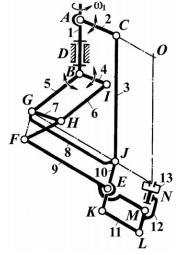
Рис.6.2 Структурна схема пантографа підвісного маніпулятора

Приклад 6.3. Визначити число ступенів вільності W просторового механізму маніпулятора (рис. 6.3).

Розв'язання.

У механізмі 4 рухомі ланки: 1, 2, 3, 4. Дві обертальні кінематичні пари V- го класу (А, D), одна сферична кінематична пара III класу (В) і

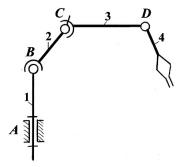
Рис.6.3. Структурна схема просторового маніпулятора

одна кінематична пара сферична з пальцем IV-го класу (С). Використовуючи формулу (4.1) для просторових механізмів визначаємо

W = 6x4-5x2-4x1-3x1 = 7.

7 СТРУКТУРНИЙ АНАЛІЗ МЕХАНІЗМІВ І КЛАСИФІКАЦІЯ

МЕХАНІЗМІВ

7.1 Вид і клас структурної групи Ассура

Клас механізму визначається найвищим класом структурної групи (групи Ассура), що входить до складу даного механізму. Структурною групою (групою Ассура) називається кінематичний ланцюг, число ступенів вільності якого відносно елементів її зовнішніх кінематичних пар дорівнює нулю, при цьому з неї не можна виділити простіші кінематичні ланцюги, що задовольняють цій умові. Згідно з визначенням числа ступенів вільності для плоских механізмів з нижчими парами

3n - 2p₅= 0,

де п - число рухомих ланок; р₅ - число однорухомих кінематичних пар V класу. Отож залежність числа кінематичних пар V класу від числа рухомих ланок в структурній групі виражається умовою

р₅=3n /2,

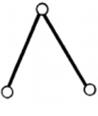
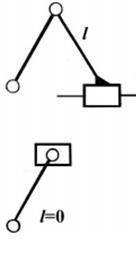
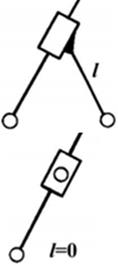
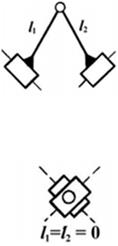
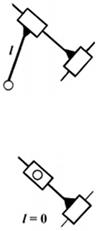
з якої виходить, що число рухомих ланок в групі Ассура має бути лише парним, тобто n = 2, 4, 6 ... Найбільш простими структурними групами є групи II класу, тобто n = 2, p₅ = 3. Залежно від розташування обертальних і поступальних кінематичних пар, групи Ассура II класу поділяються на п'ять видів (таблиця 7.1).

Клас структурних груп визначається числом кінематичних пар, що

створюють внутрішній замкнутий контур, або по числу повідців

(ланок), що приєднуються до базової ланки (таблиця 7.2).

Таблиця 7.1 Вид групи Ассура

П о р я д к о в ы й н о м е р в и д а г р у п и
1	2	3	4	5

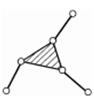
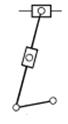
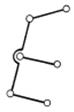
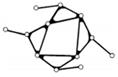
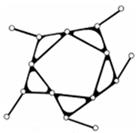
Таблиця 7.2 Класс групи Ассура

П о р я д к о в ы й н о м е р к л а с а г р у п и
III	IV	V

7.2 Порядок розв'язання завдань щодо структурного аналізу механізмів

1. Пояснити принцип роботи механізму за його кінематичною схемою, виписати номери ланок і кінематичних пар.

2. Визначити початкову ( початкові ) ланку (ланки).

3. Визначити пасивні зв'язки і зайві ступені вільності, якщо такі є в заданій схемі механізму; при необхідності побудувати кінематичну схему замінюючого механізму.

4. Перерахувати рухомі ланки і визначити їх кількість.

5. Перерахувати кінематичні пари по їх позначенням на кінематичній схемі і визначити їх клас.

6. Визначити число кінематичних пар всіх класів, утворених ланками механізму.

7. Визначити номер сімейства механізму по числу загальних зв'язків, накладених на механізм, і вказати структурну формулу.

8. Визначити ступінь вільності механізму, вказати число узагальнених координат, визначити вид незалежних рухів.

9. Виділити групи Ассура, визначити їх клас, порядок .

10. Визначити вид кінематичного ланцюга заданого механізму і клас механізму.

Для складання кінематичної схеми механізму необхідно уміти правильно креслити ланки і кінематичні пари, умовні позначення яких наведені в таблиці. 7.3.

Таблиця 7.3. Схематичне зображення ланок і кінематичних пар плоских

механізмів

Объект зображення	Умовне позначення
ланки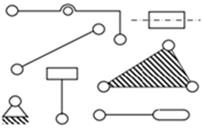
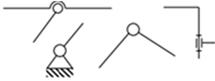
Кінематичні пари обертальні 5-го класу
Кінематичні пари поступальні 5-го класу
Кінематичні пари 4-го класу, вищі

Приклад 7.1. Виконати структурний аналіз механізму очищувача (рис.7.1).

Розв'язання. Визначимо число ступенів вільності за формулою Чебишева.

В даному механізмі число рухомих ланок п = 7 (1, 2, 3, 4, 5, 6, 7), число кінематичних пар V класу р₅ = 10:

- обертальні пари-A(0,1), B(1,2), C(2,4), D(2,3), E(0,3), F₂(5,0), G(4,6), K(6,7), L(7,0);

- поступальна пара- F₁(4,5).

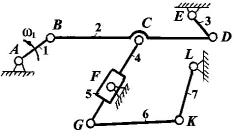
Рис.7.1 Схема механізму очищувача

Отже, після підставлення параметрів в формулу Чебишева, ступінь вільності дорівнює

W = 3 x 7 - 2 x 10 - 0 = l.

Визначимо групи Ассура, що входять до складу механізму. Початковою ланкою є кривошип 1. В першу чергу можна відокремити групу Ассура II класу першого виду, що складається з ланок 6, 7 (рис.7.2,а). Кінематичний ланцюг, що залишився, складається з ланок 1, 2, 3, 4, і 5, також є механізмом. Далі можна відокремити ланки 4 і 5, які утворюють групу Ассура II класу третього виду (рис.7.2,б).

Кінематичний ланцюг (ланки 1, 2, 3), що залишився, замкнутий і є механізмом. Відокремлюємо останню групу Ассура II класу першого виду, що складається з ланок 2, 3 (рис.7.2,в). Після цього залишається лише початкова ланка 1, яку разом із стояком 0 виділяємо в механізм 1 класу (рис.7.2,г).

а б в г

Рис.7.2. Структурні групи: а-II кл., 1 виду; б-II кл., 3 виду; в-II кл., 1 виду; г-механізм 1-го класу;

Складемо формулу будови механізму

I (0, 1) →II (2, 3) →II (4, 5) → II (6, 7).

До складу даного механізму входять структурні групи Ассура, найвищий клас яких другий, отже, механізм відноситься до другого класу.

Приклад 7.2. Виконати структурний аналіз механізму двигуна (рис. 7.3, а),якщо початковою ланкою є кривошип ОА.

Розв'язання. Механізм складається із семи рухомих ланок (n = 7) і десяти пар V класу (р₅ = 10): 0(0, 1), А(1, 2), В(2, 3), В₀(3,0) С(2, 4), D(4, 5), Е(5, 0), F(5, 6), G(6, 7), G₀(7, 0). Знаходимо ступінь вільності механізму за формулою Чебишева.

W = 3 n - 2p₅ - p₄ =3 × 7 - 2 × 10 - 0 = 1.

У цьому механізмі також повинна бути одна початкова ланка; зайвих зв'язків і ступенів вільності, а також пар IV класу немає.

Розкладаємо механізми на групи Ассура. Якщо початковою ланкою є кривошип 1, який із стояком 0 утворює механізм 1 класу (рис. 7.3, д),то решта ланок утворюють три структурні групи II класу II порядку (рис. 7.3, б,в,г).Такий механізм належить до механізму II класу. Формула його будови має вигляд

I(1)→ II(2,3) →II(4, 5) → II(6, 7).

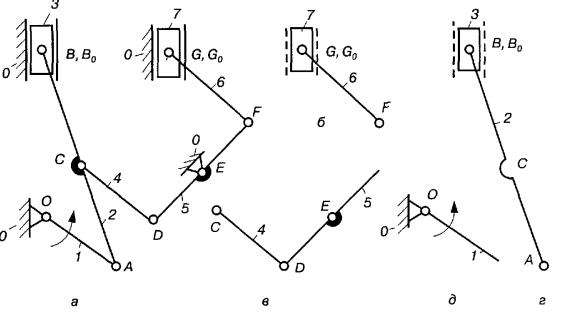
Рис. 7.3. Структурна схема двигуна; 1- початкова ланка

Якщо вибрати початковою ланкою, наприклад, ланку 7 (рис.7.3,а), то механізм треба віднести до III класу, тому що у цьому випадку ланки і кінематичні пари, до складу яких вони входять, утворюють дві групи, одна з них група III класу (рис. 7.4, а), друга — II класу (рис. 7.4, б). Повзун 7 (рис. 7.4, в) разом із стояком 0 утворює механізм І класу.

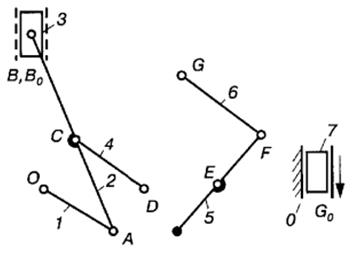
а б в

Рис.7.4. Структурні групи двигуна; 7- початкова ланка

Формула будови такого механізму має вигляд

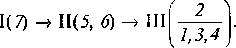
Тут у групі ІII -го класу окремо виділена базисна ланка 2. При початковій ланці 5 механізм також буде III класу, формулу будови якого можна записати так:

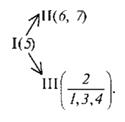
Приклад 7.3.

Метою даного прикладу є визначення ступеня рухомості кінематичного ланцюга, з'ясування, чи є даний кінематичний ланцюг механізмом, виділення структурних груп і визначення класу механізму.

Розв'язання.У даному завданні запропонований замкнутий плоский складний кінематичний ланцюг з початковою ланкою 1, представлений на структурній схемі (рис.7.5), що має 4 рухомих ланки:

1 - початкова ланка;

2 - ролик;

3 - шатун;

4 - коромисло.

Ланки сполучені кінематичними парами. Встановимо характеристику кінематичних пар, визначимо їх клас (табл.7.4).

⇐ Предыдущая 1 234 5 6 Следующая ⇒