Лабораторная работа. Матричное представление элементов симметрии. Цель работы. Теоретическая часть

Лабораторная работа

Матричное представление элементов симметрии

Цель работы

Ознакомление студентов с примерами и принципами описания преобразований симметрии в кристалле.

Теоретическая часть

Кристалл можно связать с некоторой трехмерной системой координат, например, декартовой. Операции симметрии можно представить в виде матричных преобразований этих координат. При этом старые координаты переходят в новые координаты

x, y, z ® x', y', z'

Это преобразование можно записать в следующем общем виде

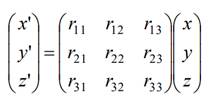
Матрица называется матрицей симметричного преобразования, то есть она показывает, как нужно повернуть или отразить старую систему координат вокруг оси симметрии или в плоскости, что бы получить новую систему координат.

Рассмотрим примеры матриц преобразований.

Матрица поворота на 360 градусов выглядит так

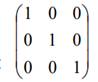
Матрица инверсии выглядит так

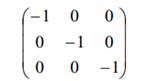
Матрицы преобразования при зеркальном отражении в плоскости, перпендикулярной оси Ох, выглядит так

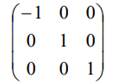
Матрица преобразования при повороте на угол π радиан (180⁰) в декартовой системе координат вокруг оси, параллельной оси Оz, выглядит так

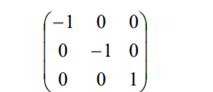
Для подробного описания преобразований симметрии записывают так называемую расширенную матрицу или таблицу, в которую вносят углы между старыми и новыми координатными осями.

Например, изобразим поворот вокруг оси Оz на 180 градусов.

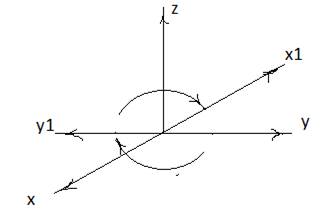
Преобразование поворотом вокруг оси Оz на 180 градусов

Запишем таблицу из углов между старыми и новыми координатными осями и косинусами этих углов

Табличная запись поворота вокруг оси ОZ на 180 градусов или π рад

Правая часть таблицы из косинусов и будет матрицей преобразования при повороте на угол π радиан (180⁰) в декартовой системе координат вокруг оси, параллельной оси Оz.

Определим матрицу поворота на 90 градусов вокруг оси Оz. Сначала изобразим преобразование с помощью рисунка. Затем запишем таблицу из углов между старыми и новыми координатными осями и косинусами этих углов

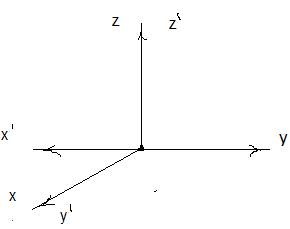
Преобразование поворотом вокруг оси Оz на 90 градусов

Табличная запись поворота вокруг оси ОZ на 90 градусов

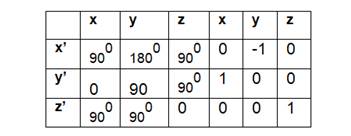
Экспериментальная часть

1.Построить изображение и записать матрицы отражения в плоскостях, перпендикулярных осям Оy и Oz.

2.Построить изображение и записать матрицы поворота вокруг осей Оу и Ох на 180 градусов.

3. Построить изображение и записать матрицу поворота вокруг осей Оz на 90 градусов в другую сторону.

4. Построить изображение и записать матрицы поворота вокруг осей Оу и Ох на 90 градусов в обе стороны.

5. Записать матрицу отражения в начале координат.

12 3 4 5 6 Следующая ⇒