
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Диофантовы уравнения 5 страница
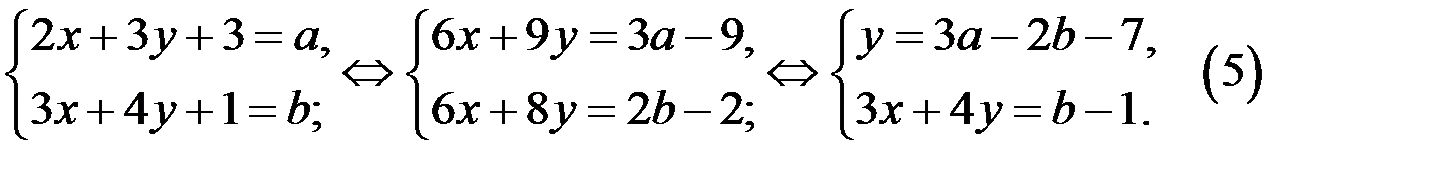
Система (5) может иметь решение, если 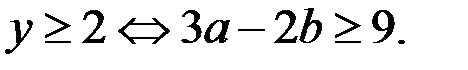
Легко проверить, что условие 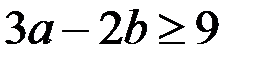 выполняется только для пары
выполняется только для пары 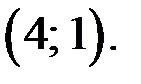
Если 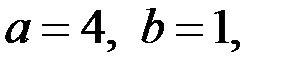 то система (5) принимает вид
то система (5) принимает вид
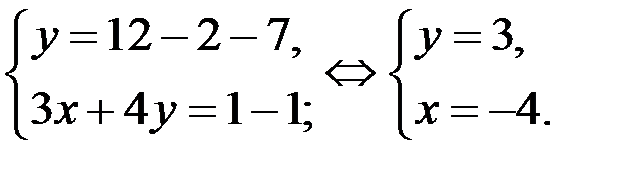
Итак, решением системы (5), а значит и исходного уравнения является пара чисел 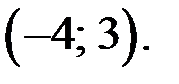
Ответ. 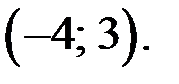
71.Найдите все целые решения уравнения
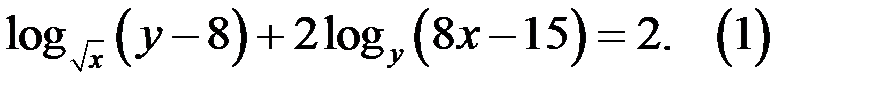
Решение. 1. Так как 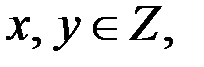 то ОДЗ уравнения удовлетворяет системе неравенств:
то ОДЗ уравнения удовлетворяет системе неравенств:
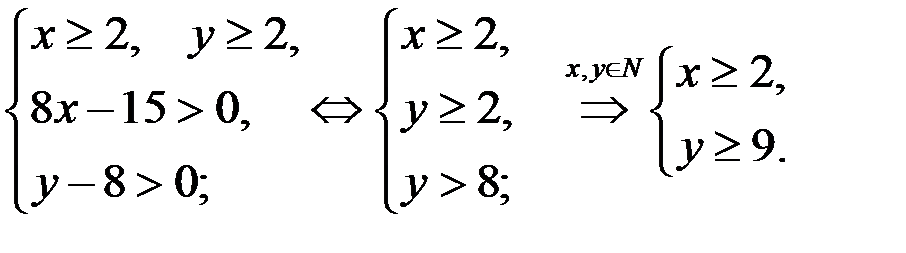
Уравнение (1) равносильно уравнению
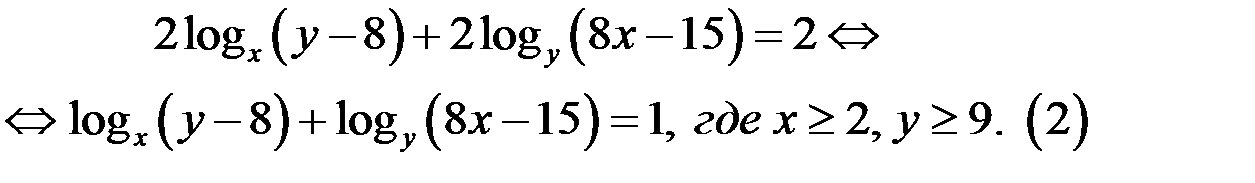
Уравнение (2), а значит и уравнение (1), может иметь решение в целых числах, если х и у, удовлетворяют системе неравенств
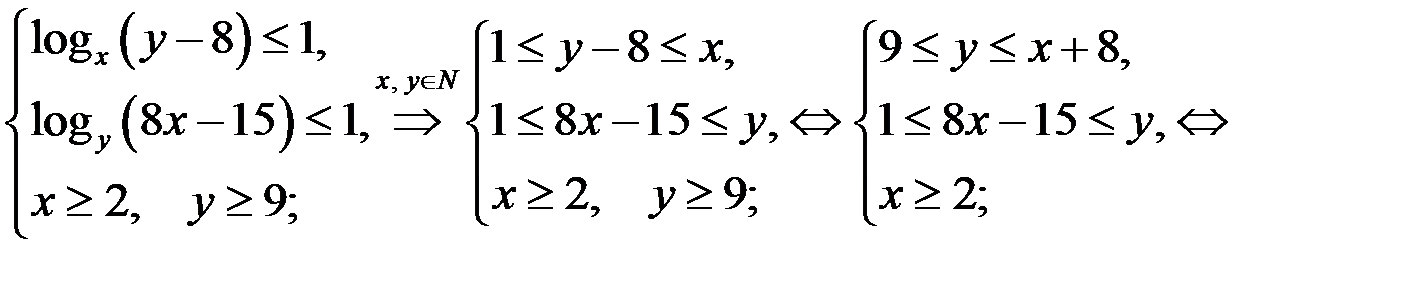
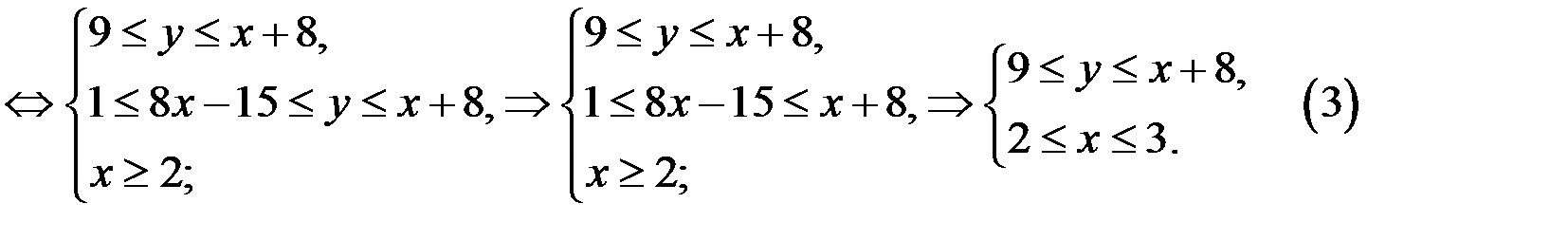 Из системы (3) следует, что
Из системы (3) следует, что 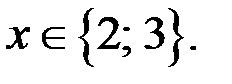
2. Решим уравнение (2), если 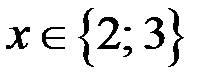 и
и 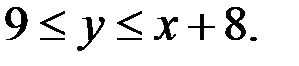
1) Если 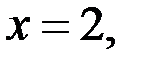 то уравнение (2) принимает вид
то уравнение (2) принимает вид
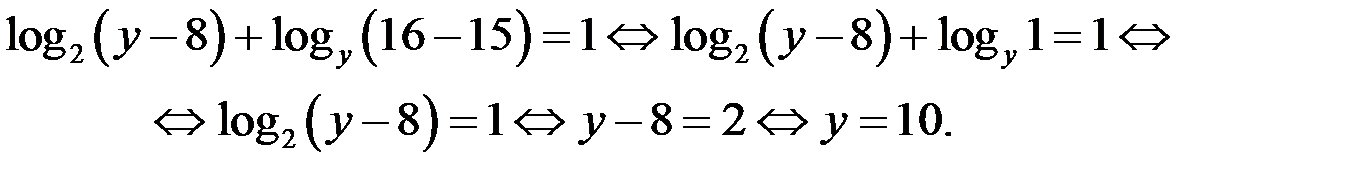
Пара чисел 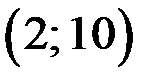 является решением уравнения (2), а значит и уравнения (1).
является решением уравнения (2), а значит и уравнения (1).
2) Если 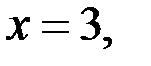 то из двойного неравенства
то из двойного неравенства 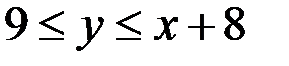 следует, что
следует, что 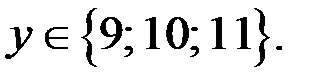
Найдём решения уравнения (2), если 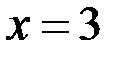 и
и 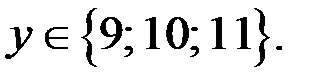
а) Если 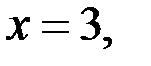
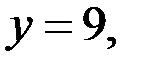 то уравнение (2) принимает вид
то уравнение (2) принимает вид 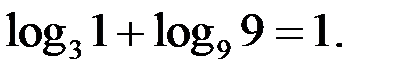 Решением уравнения (2), а значит и уравнения (1) является пара чисел
Решением уравнения (2), а значит и уравнения (1) является пара чисел 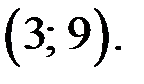
б) Если 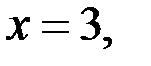
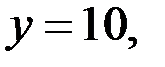 то уравнение (2) принимает вид
то уравнение (2) принимает вид 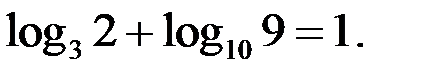
Оценим 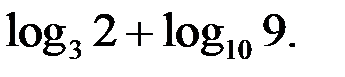
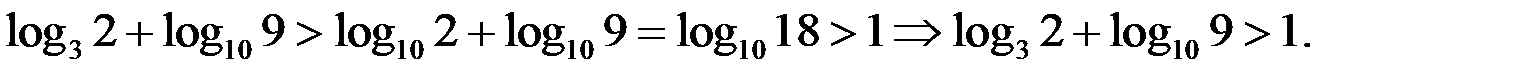
Так как 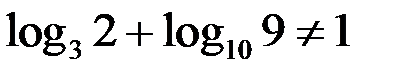 , то уравнение (2) не имеет решений. Тогда и уравнение (1) не имеет решений.
, то уравнение (2) не имеет решений. Тогда и уравнение (1) не имеет решений.
в) Если 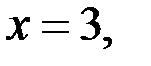
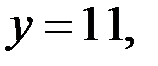 то уравнение (2) принимает вид
то уравнение (2) принимает вид
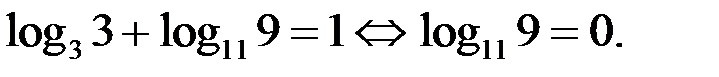
Так как 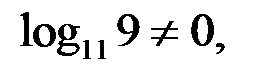 то уравнение (2) не имеет решений. Тогда и уравнение (1) не имеет решений.
то уравнение (2) не имеет решений. Тогда и уравнение (1) не имеет решений.
Ответ. 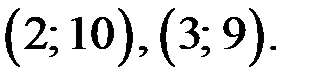
72. Решите в целых числах уравнение
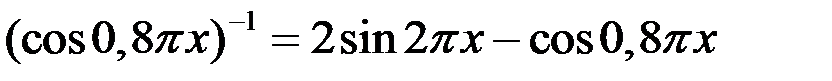 .
.
Решение. 1. Очевидно, исходное уравнение равносильно уравнению 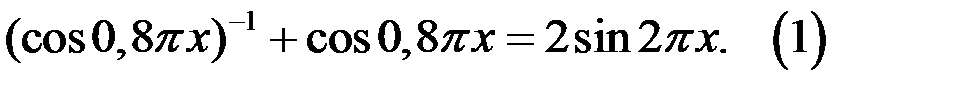
Отметим: 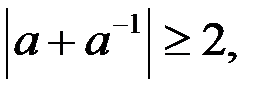 где а
где а 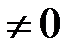 ;
; 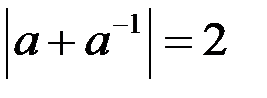 тогда и только тогда, когда
тогда и только тогда, когда 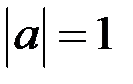 .
.
Так как 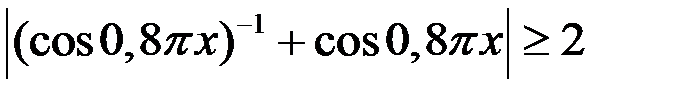 и
и 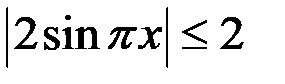 , то уравнение (1) равносильно системе:
, то уравнение (1) равносильно системе:
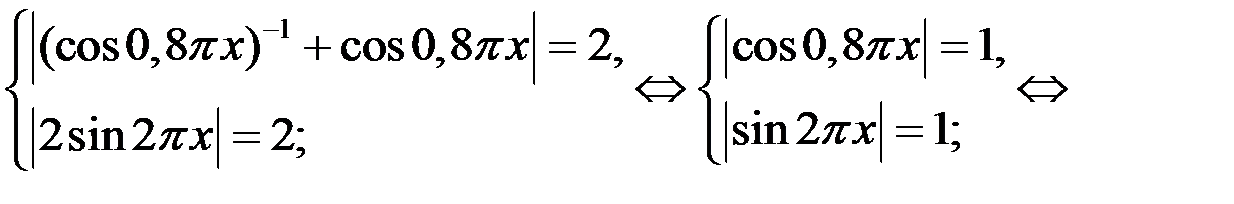
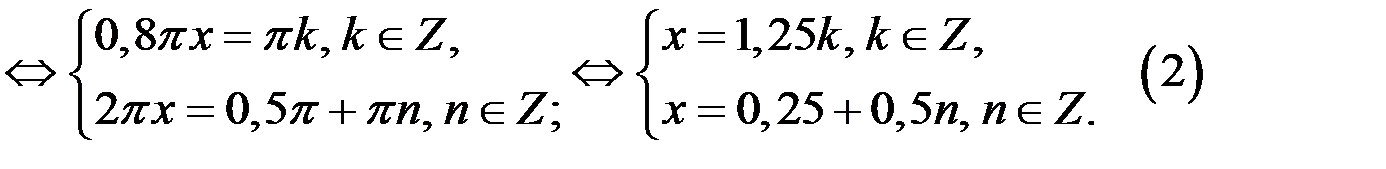
2. Рассмотрим второе уравнение системы (2). Имеем:
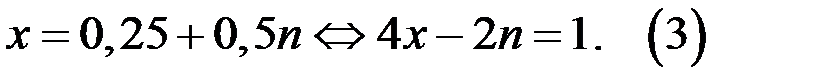
Так как в уравнении (3) коэффициенты при х и n имеют общий множитель, равный 2, но свободный член не делится на 2, то уравнение (3), а значит и система (2), а также и исходное уравнение, не имеют решений в целых числах.
Ответ. Уравнение, не имеют решений в целых числах.
73. Решите уравнение 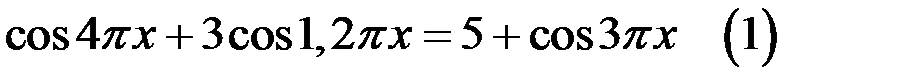 в
в
целых числах.
Решение. 1. Так как 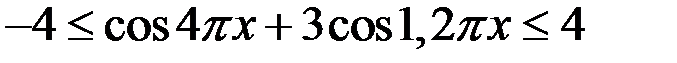 ,
, 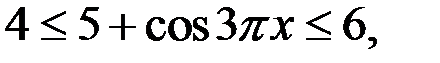 то левая часть уравнения не больше 4, а правая
то левая часть уравнения не больше 4, а правая 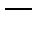 не меньше 4. Тогда уравнение (1) равносильно системе
не меньше 4. Тогда уравнение (1) равносильно системе
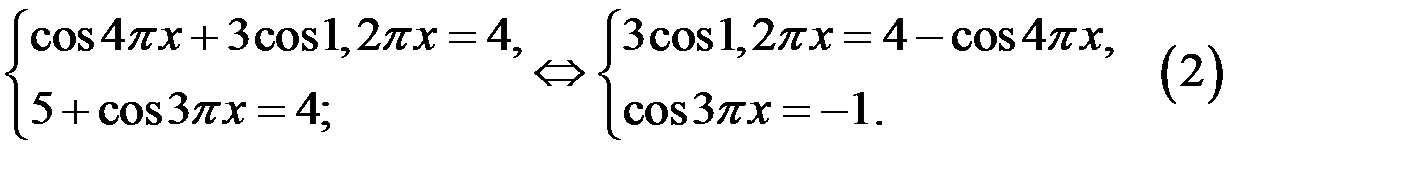
2. Рассмотрим уравнение 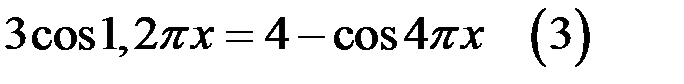 .
.
Так как 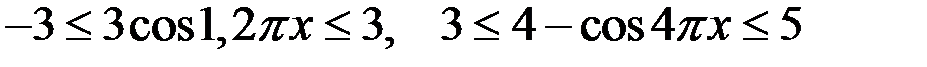 , то левая часть уравнения (3) не больше 3, а правая
, то левая часть уравнения (3) не больше 3, а правая 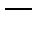 не меньше 3. Тогда уравнение (3) равносильно системе
не меньше 3. Тогда уравнение (3) равносильно системе
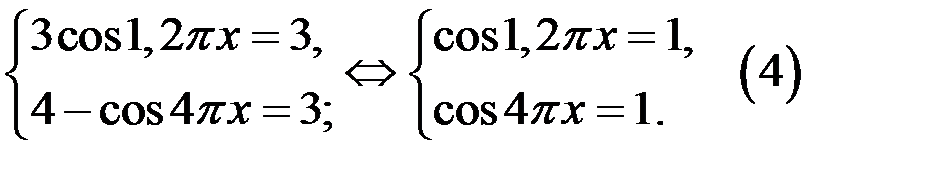
Из систем (2) и (4) следует, что уравнение (1) равносильно системе
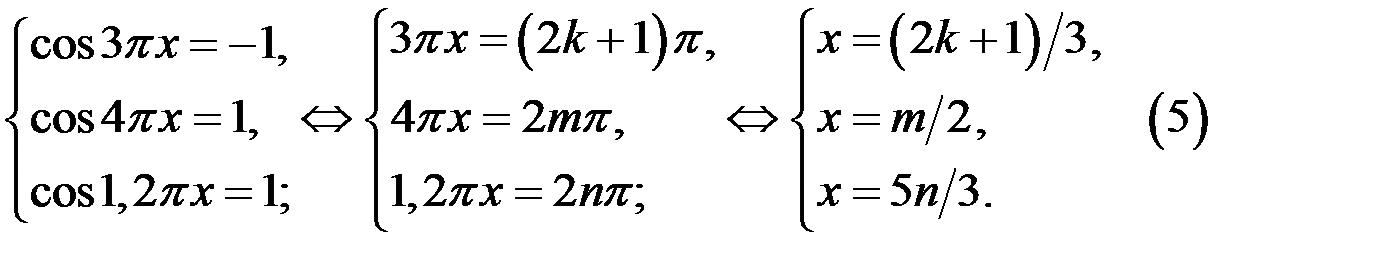
а) Для того чтобы найти целое значение х, которое удовлетворяет системе (5) сначала рассмотрим, например, систему
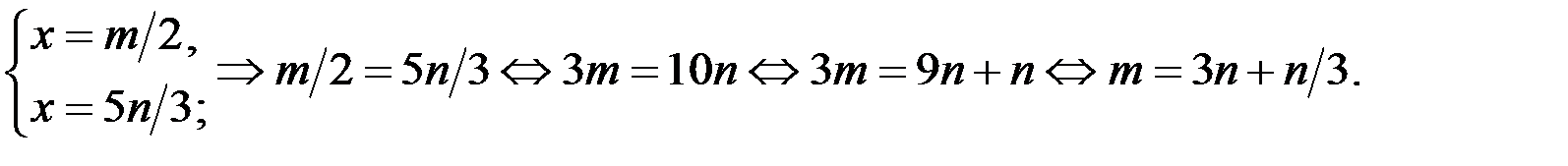 Число т будет целым числом, если существует число
Число т будет целым числом, если существует число 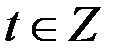 такое, что
такое, что 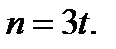 Так как
Так как 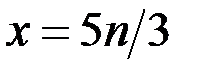 и
и 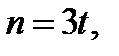 то
то 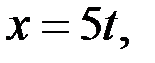 где
где 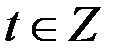 .
.
б) Рассмотрим систему
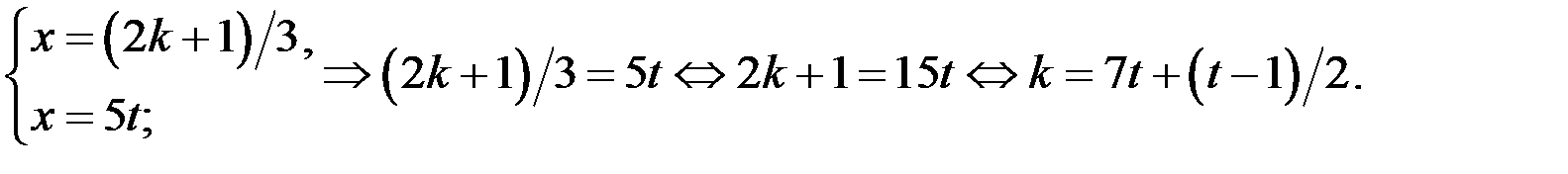
Число 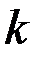 будет целым числом, если существует число
будет целым числом, если существует число 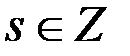 такое,
такое, 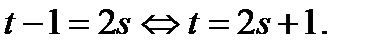 Так как
Так как 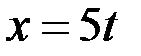 и
и 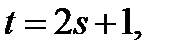 то
то 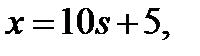 где
где 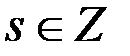 .
.
Ответ. 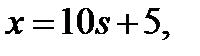 где
где 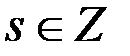 .
.
.74. Решите в целых числах уравнение
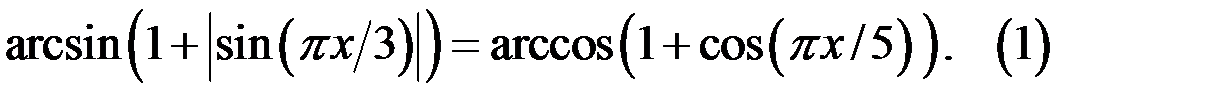 .
.
Решение. 1. ОДЗ уравнения удовлетворяет системе неравенств:
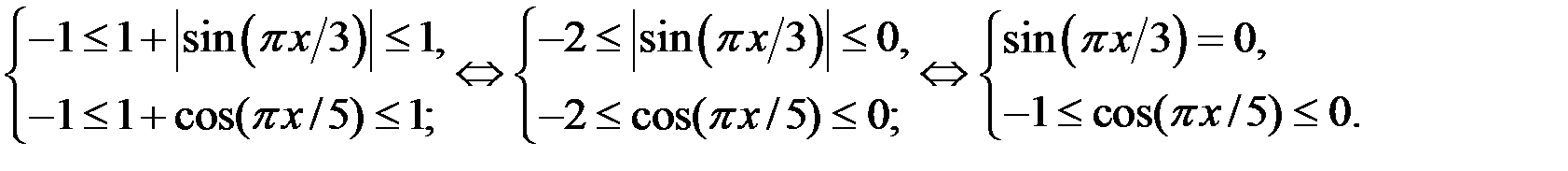
Если 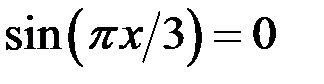 , то
, то 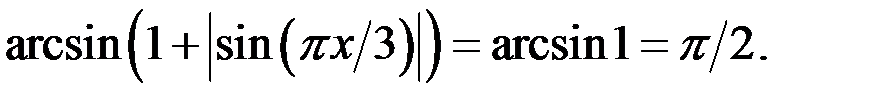 Тогда с учётом ОДЗ, уравнение (1) равносильно уравнению
Тогда с учётом ОДЗ, уравнение (1) равносильно уравнению
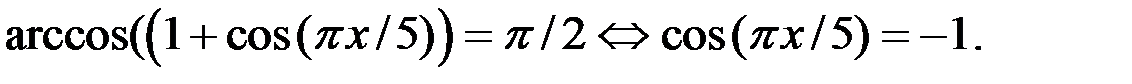
С учётом ОДЗ решение уравнения (1) находится из системы
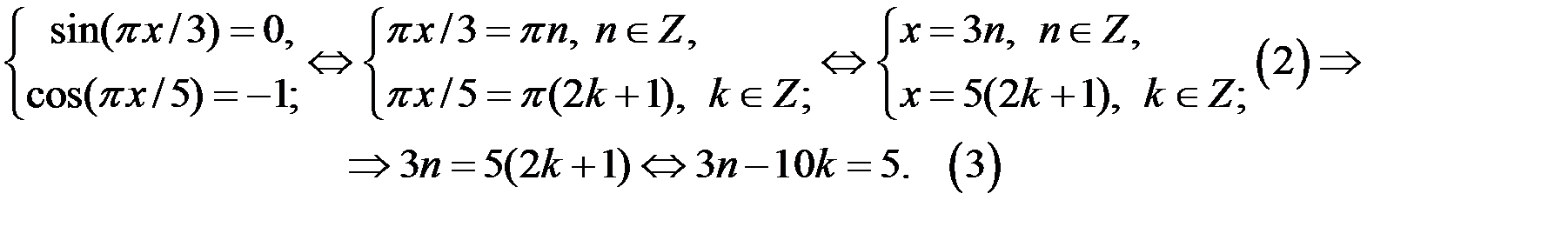 Уравнение
Уравнение 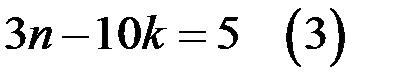 имеет решение в целых числах, так как коэффициенты при k и n взаимно простые числа.
имеет решение в целых числах, так как коэффициенты при k и n взаимно простые числа.
2. Найдём в целых числах решение уравнения (3).
а) Преобразуем уравнение (выразим n через k):
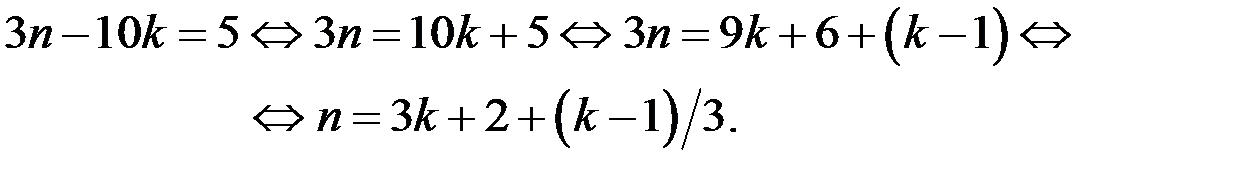
Число n будет целым числом, если существует число 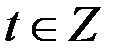 такое, что
такое, что 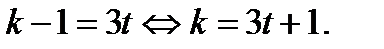
б) Так как из системы (2) следует, что 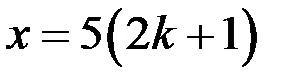 и
и 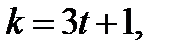 то
то 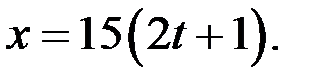
Ответ. 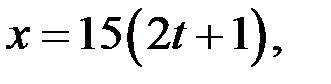 где
где 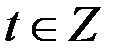 .
.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|