
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Диофантовы уравнения 4 страница
Сумма неотрицательных чисел равна нулю только в случае, если каждое слагаемое равно нулю. Поэтому уравнение (2), а значит и уравнение (1) равносильно системе уравнений
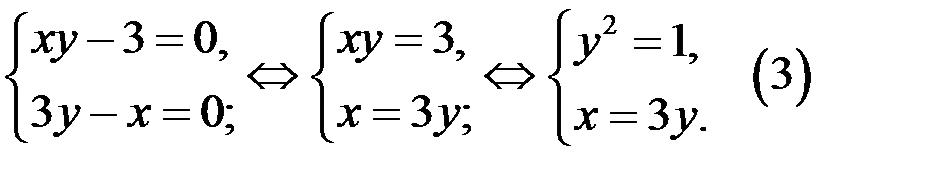
Из первого уравнения системы (3) следует, что 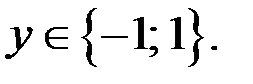 Так как
Так как 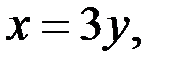 то решениями системы (3), а значит и исходного уравнения, являются пары
то решениями системы (3), а значит и исходного уравнения, являются пары 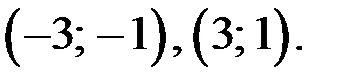
Ответ. 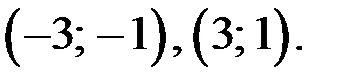
62. Решите в целых числах уравнение
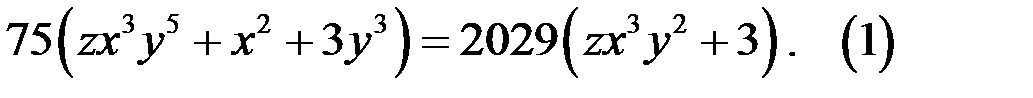
Решение. Докажем, что 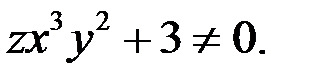
Если 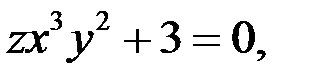 то
то 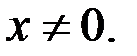 Если
Если 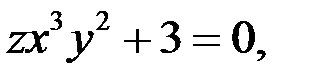 то из уравнения (1) следует, что
то из уравнения (1) следует, что 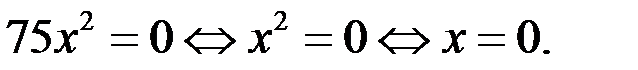
Предположение, что 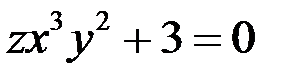 , привело к противоречию.
, привело к противоречию.
Таким образом, 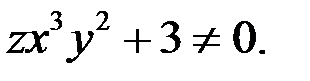 Тогда уравнение (1) равносильно уравнению
Тогда уравнение (1) равносильно уравнению
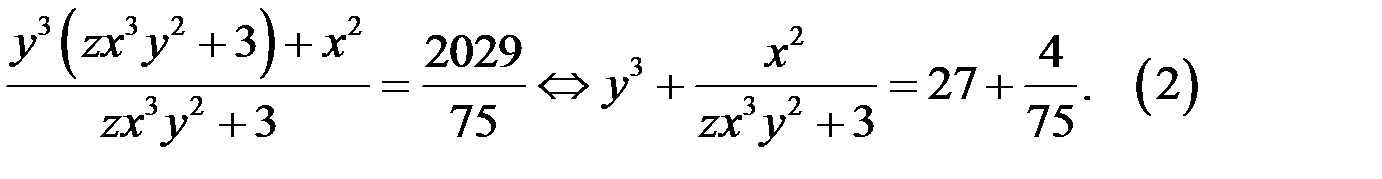
Найдём целые решения уравнение (2).
1. Сначала докажем, что
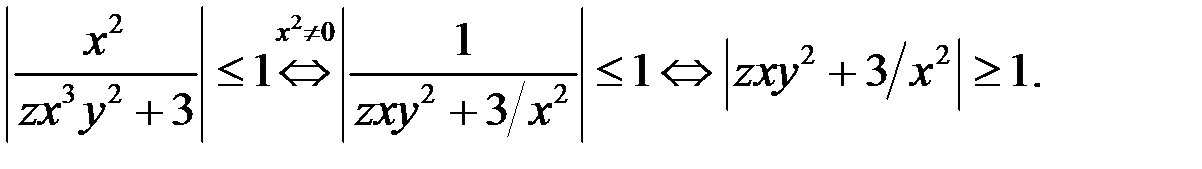
а) Пусть 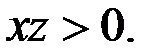 Так как
Так как 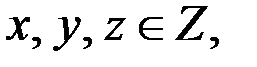 то
то
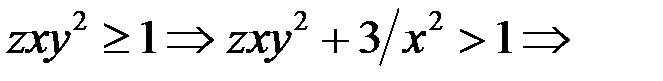
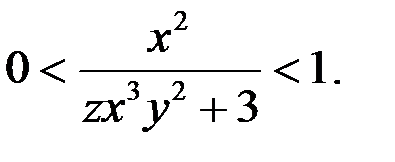
б) Пусть 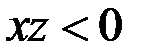 и
и 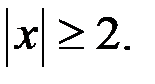 Так как
Так как 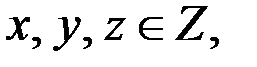 то
то 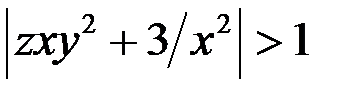 .
.
Пусть 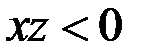 и
и 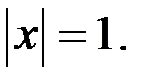 Так как
Так как 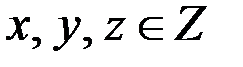 и
и 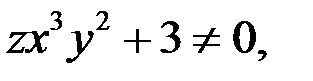 то
то 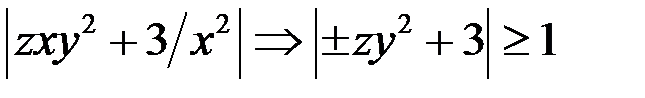 . Итак, если
. Итак, если 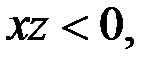 то
то 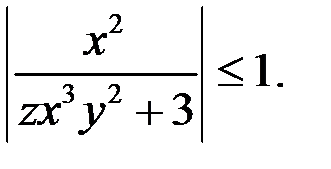
в) Если 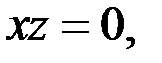 то уравнение (1) не имеет решений, так как это уравнение принимает вид
то уравнение (1) не имеет решений, так как это уравнение принимает вид 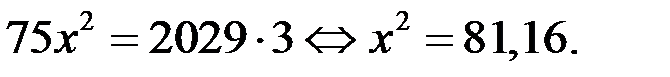
2. Найдём целые решения уравнения
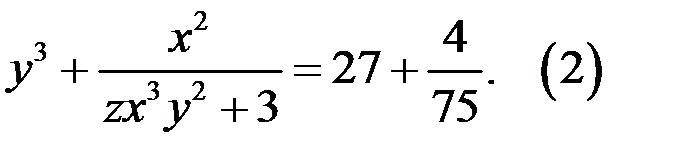
а) Если 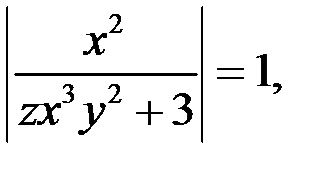 то уравнение (2) не имеет решений в целых числах, так как левая часть уравнения (2) целое число
то уравнение (2) не имеет решений в целых числах, так как левая часть уравнения (2) целое число 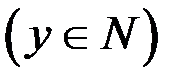 , а правая часть не является целым числом.
, а правая часть не является целым числом.
б) Если 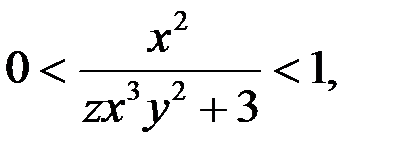 то
то
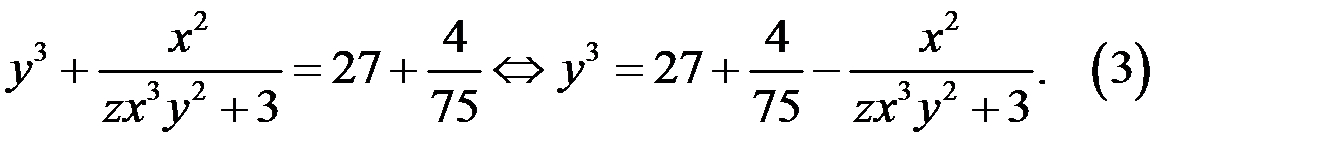
Так как 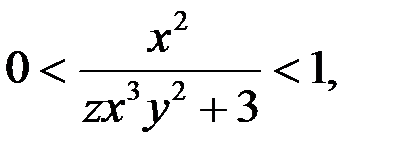 то из уравнения (3) следует, что
то из уравнения (3) следует, что 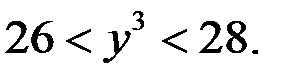 Уравнение (3) может иметь решение, если
Уравнение (3) может иметь решение, если 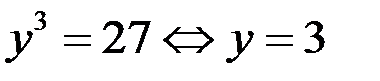 и
и
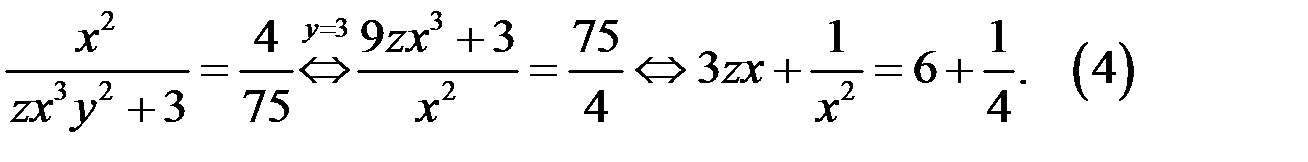
Из уравнения (4) следует, что 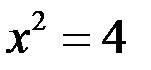 и
и 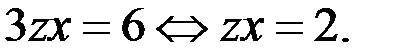
Если 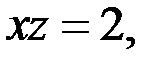
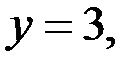
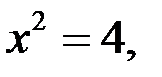 то решениями уравнения (4), а значит и уравнения (1), являются тройки чисел
то решениями уравнения (4), а значит и уравнения (1), являются тройки чисел 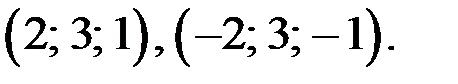
Если 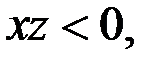 то уравнения (4), а значит и уравнения (1), не имеет решений, так как
то уравнения (4), а значит и уравнения (1), не имеет решений, так как 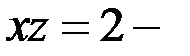 положительное число.
положительное число.
в) Если 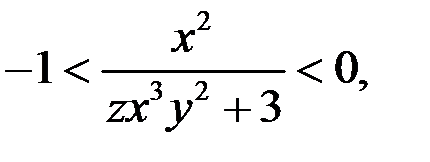 то
то
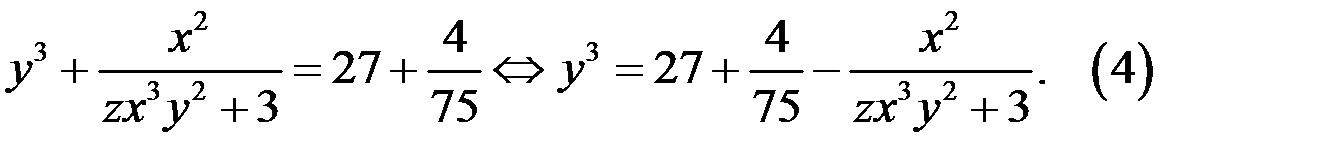
Так как 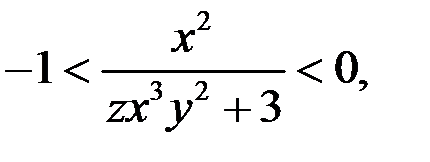 то из уравнения (4) следует, что
то из уравнения (4) следует, что 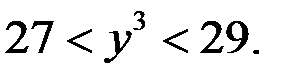 Очевидно, не существует целого числа, удовлетворяющему условию
Очевидно, не существует целого числа, удовлетворяющему условию 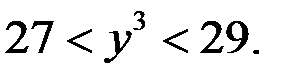
Ответ. 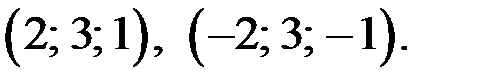
63. Докажите, что множество решений уравнения 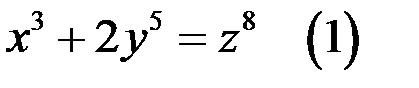 в натуральных числах бесконечно.
в натуральных числах бесконечно.
Решение.1. Пусть 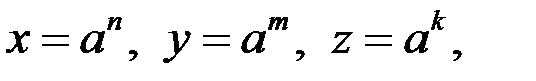 где
где 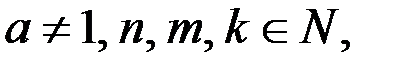 удовлетворяют уравнению (1). Тогда имеем
удовлетворяют уравнению (1). Тогда имеем
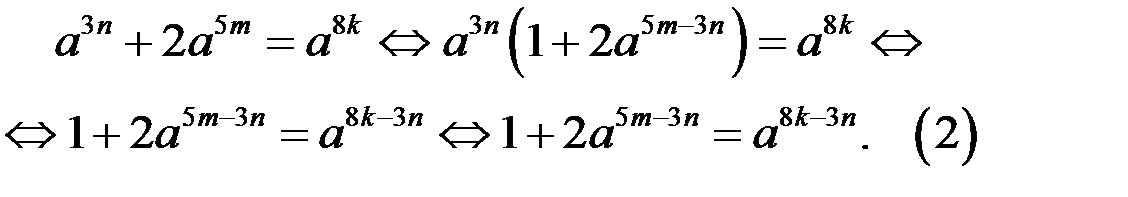
Найдём значения 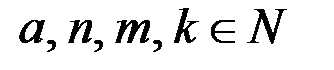 такие, что
такие, что 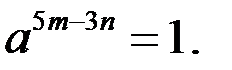 Тогда уравнение (2) равносильно системе
Тогда уравнение (2) равносильно системе
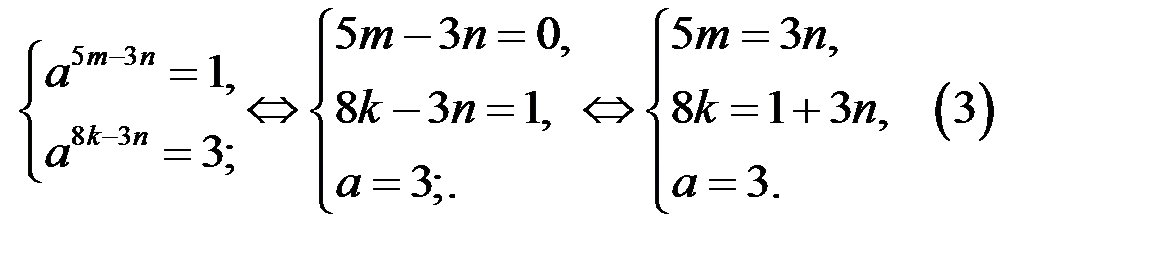
Так как, например, 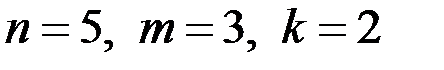 удовлетворяют системе (3), то решением уравнения (1) является тройка чисел
удовлетворяют системе (3), то решением уравнения (1) является тройка чисел 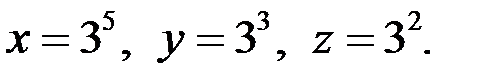
2. Найдём значения 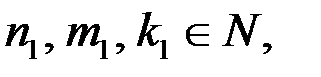 при которых тройка чисел
при которых тройка чисел 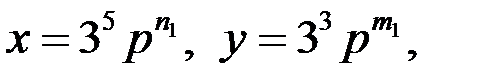
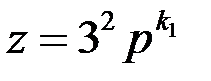 является решением уравнения (1) при любых натуральных значениях р. Имеем
является решением уравнения (1) при любых натуральных значениях р. Имеем
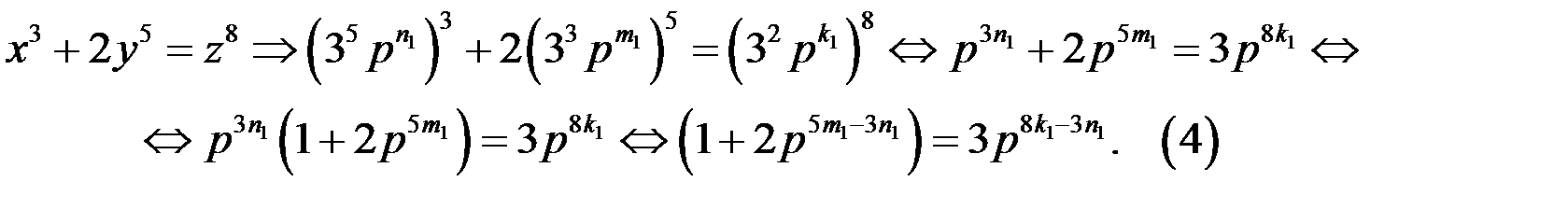 Уравнение (4) имеет решение, например, если
Уравнение (4) имеет решение, например, если
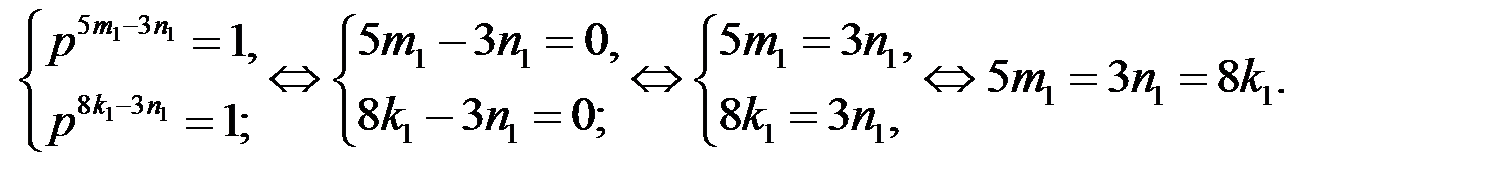
Так как НОК(3; 5; 8)=120, то
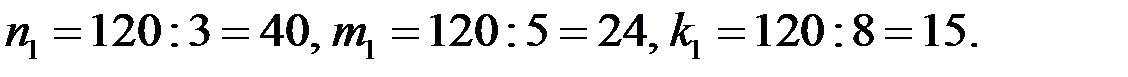
Итак, тройка чисел 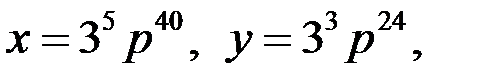
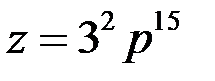 является решением уравнения (1) при любых натуральных значениях р.
является решением уравнения (1) при любых натуральных значениях р.
Ответ. Решений уравнения в натуральных числах бесконечно.
64. Докажите, что множество решений уравнения 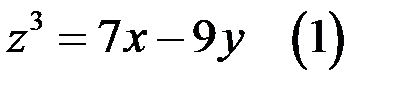 в целых числах бесконечно.
в целых числах бесконечно.
Решение. Пусть 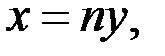 где
где 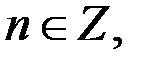 удовлетворяет уравнению (1). Тогда имеем
удовлетворяет уравнению (1). Тогда имеем 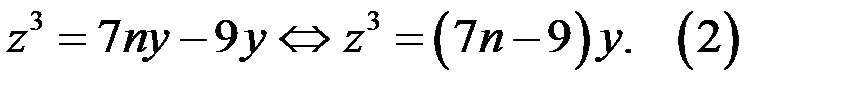
Так как число 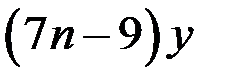 равно кубу целого числа, то из уравнения (2) следует: если, например,
равно кубу целого числа, то из уравнения (2) следует: если, например, 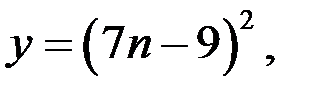 то
то 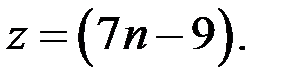 И так как
И так как 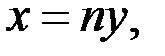 то
то 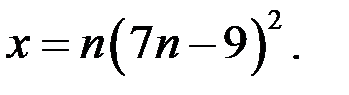
Так как тройка чисел 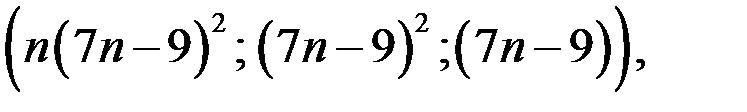 где
где 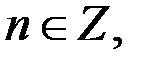 является решением уравнению (2), то она решение и уравнения (1).
является решением уравнению (2), то она решение и уравнения (1).
Ответ. Решений уравнения в целых числах бесконечно.
65. Решите уравнение 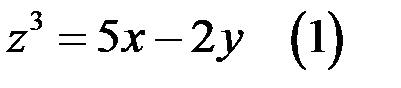 в целых числах.
в целых числах.
Решение.1. Имеем 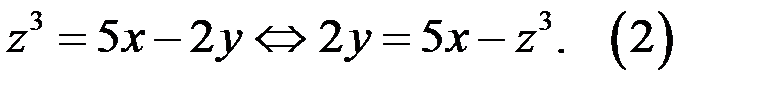
Так как левая часть уравнение (2) чётное число, то уравнение может иметь решение, если и правая часть чётное число. Возможны два случая.
1. Если 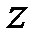 и
и 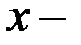 чётные числа, то существуют числа
чётные числа, то существуют числа 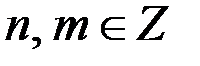 такие, что
такие, что 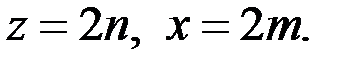 Тогда уравнение (2) принимает вид
Тогда уравнение (2) принимает вид
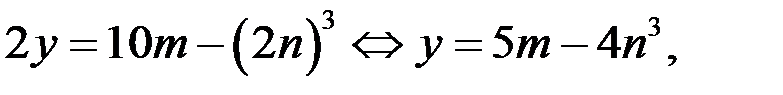 где
где 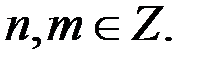
Таким образом, решением исходного уравнения является тройка 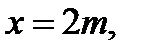
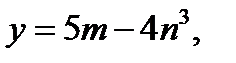
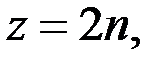 где
где 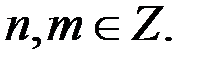
2. Если 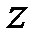 и
и 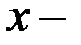 нечётные числа, то существуют числа
нечётные числа, то существуют числа 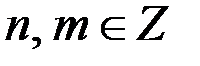 такие, что
такие, что 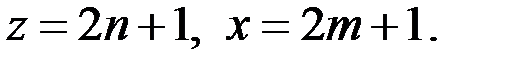 Тогда уравнение (2) принимает вид
Тогда уравнение (2) принимает вид
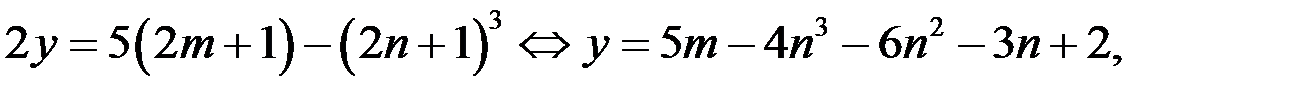 где
где 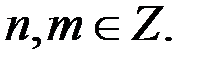
Таким образом, решением исходного уравнения является тройка 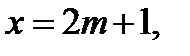
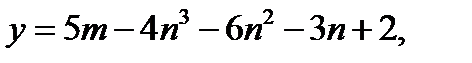
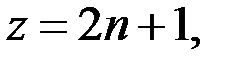 где
где 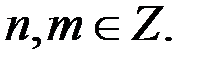
Ответ. 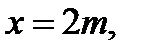
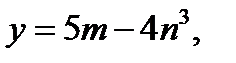
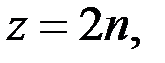 где
где 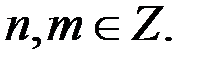
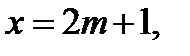
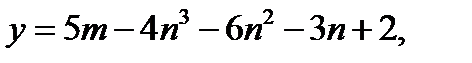
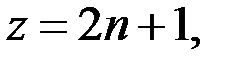 где
где 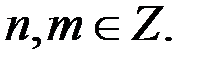
66. Докажите, что уравнение 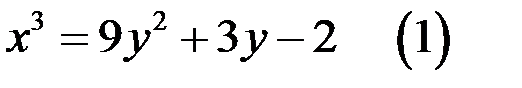 не имеет решений в целых числах.
не имеет решений в целых числах.
Решение. 1. Преобразуем уравнение (1):
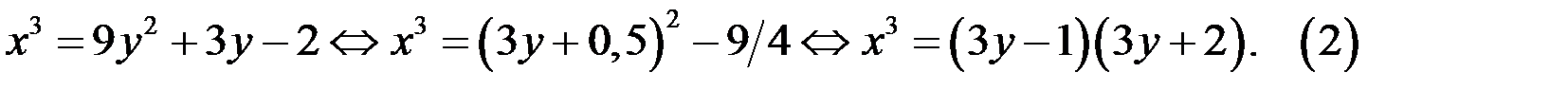
2. Докажем, что числа 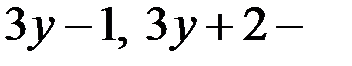 взаимно простые.
взаимно простые.
Будем доказывать от противного.
Пусть числа 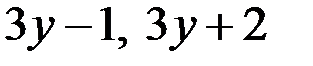 не являются взаимно простыми. Тогда существуют числа
не являются взаимно простыми. Тогда существуют числа 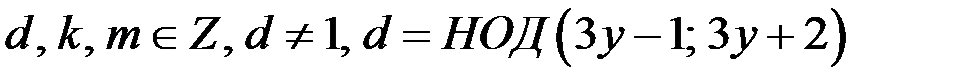 такие, что
такие, что 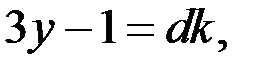
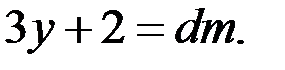 Тогда
Тогда
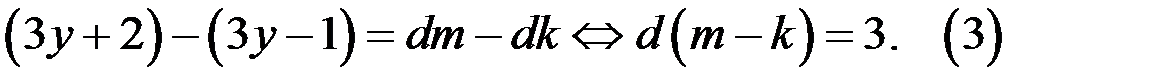
а) Из уравнения (3) следует, что 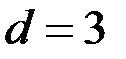 и
и 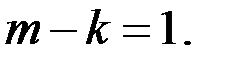 Если
Если 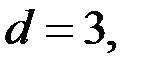 то
то 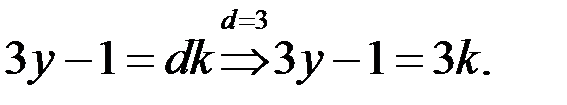 Последнее уравнение не имеет решений, так как правая часть этого равенства делится на 3, а левая–не делится на 3. Итак,
Последнее уравнение не имеет решений, так как правая часть этого равенства делится на 3, а левая–не делится на 3. Итак, 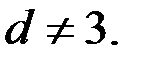
б) Из уравнения (3) следует, что 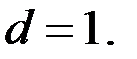 По предположение числа
По предположение числа 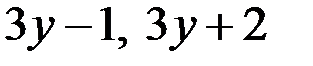 не являются взаимно простыми. Тогда
не являются взаимно простыми. Тогда 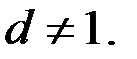 Предположение, что числа
Предположение, что числа 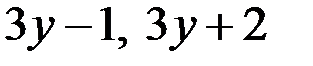 не являются взаимно простыми, привело к противоречию.
не являются взаимно простыми, привело к противоречию.
Из а) и б) следует: числа 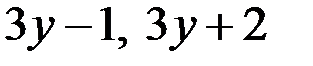 являются взаимно простыми.
являются взаимно простыми.
3. Если произведение взаимно простых чисел равно кубу целого числа, то каждое из этих чисел является кубом целого числа. Тогда существуют числа 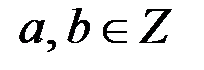 такие, что
такие, что
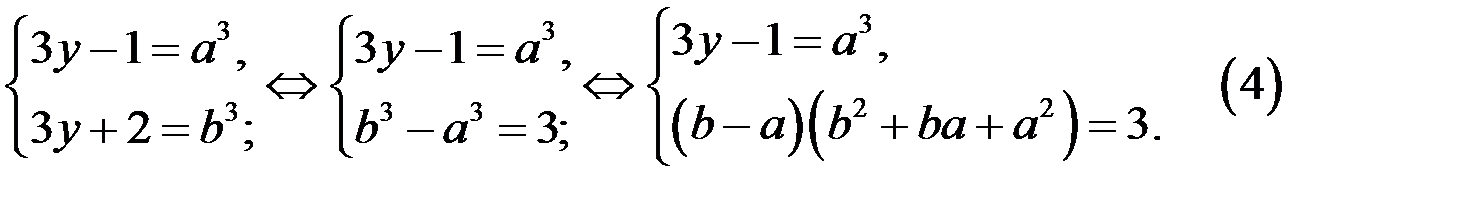
Так как 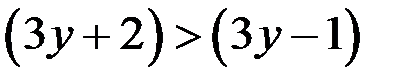 , то
, то 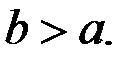 Тогда второе уравнение системы (4) равносильно системе
Тогда второе уравнение системы (4) равносильно системе
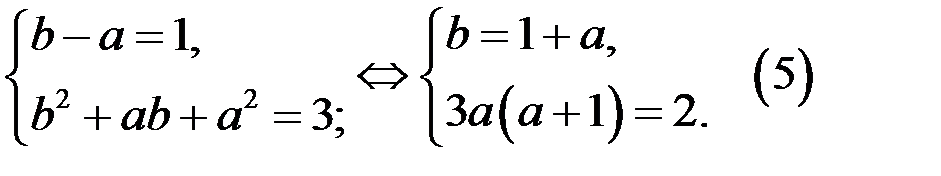
Так как левая часть уравнения 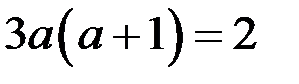 кратна 3, а правая – не кратна 3, то система (5), а значит и уравнение (1), не имеет решений.
кратна 3, а правая – не кратна 3, то система (5), а значит и уравнение (1), не имеет решений.
Ответ. Уравнение не имеет решений в целых числах.
67. Решите уравнение 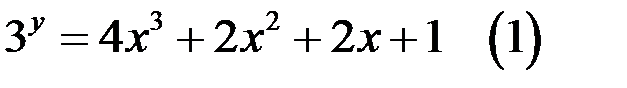 в целых числах.
в целых числах.
Решение. 1. Очевидно,
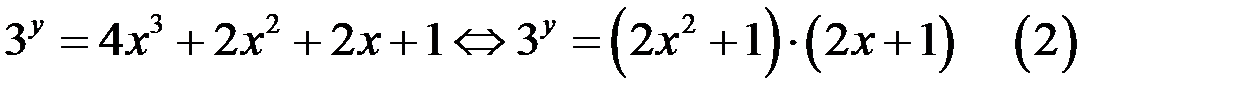
Отметим, так как 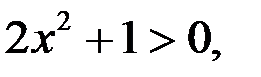 то из уравнения (2) (левая часть уравнения (2) является положительной) следует, что
то из уравнения (2) (левая часть уравнения (2) является положительной) следует, что 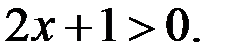
Так как правая часть уравнения (2) является целым числом, то и левая часть – целое число. Тогда 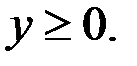 Так как левая часть уравнения (2) является неотрицательной степенью числа 3, то каждая из скобок левой части является неотрицательной степенью числа 3. Тогда из уравнения (2) следует: существуют неотрицательные числа
Так как левая часть уравнения (2) является неотрицательной степенью числа 3, то каждая из скобок левой части является неотрицательной степенью числа 3. Тогда из уравнения (2) следует: существуют неотрицательные числа 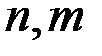 такие, что
такие, что
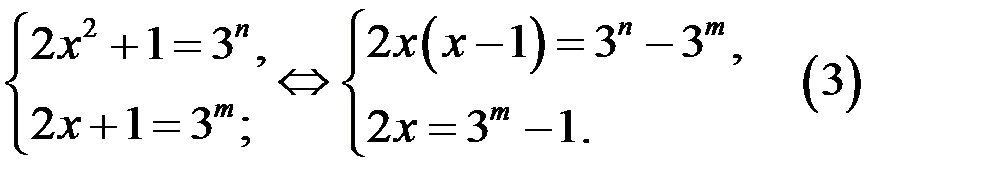
2. Рассмотрим систему (3).
а) Если 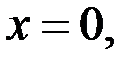 то
то
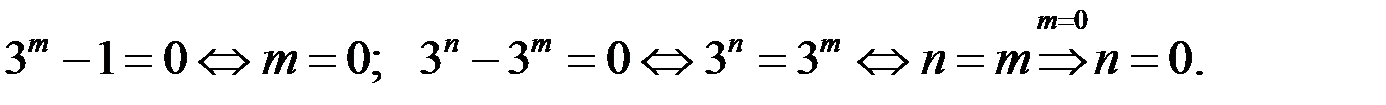
Если 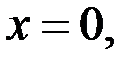 то из уравнения (1) находим, что
то из уравнения (1) находим, что 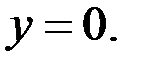 Пара чисел
Пара чисел 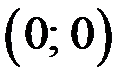 является решением уравнения (1). Итак, если
является решением уравнения (1). Итак, если 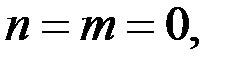 то уравнение (1) имеет решение в целых числах.
то уравнение (1) имеет решение в целых числах.
б) Если 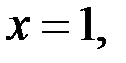 то
то
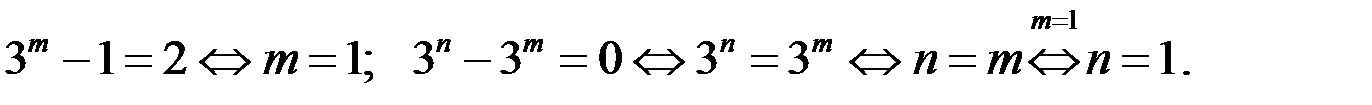
Если 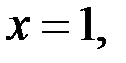 то из уравнения (1) находим, что
то из уравнения (1) находим, что 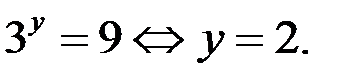 Пара чисел
Пара чисел 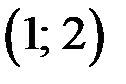 является решением уравнения (1). Итак, если
является решением уравнения (1). Итак, если 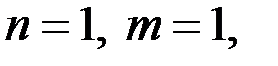 то уравнение (1) имеет решение в целых числах.
то уравнение (1) имеет решение в целых числах.
в) Пусть 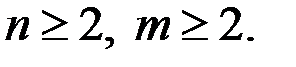 Преобразуем систему (3).
Преобразуем систему (3).
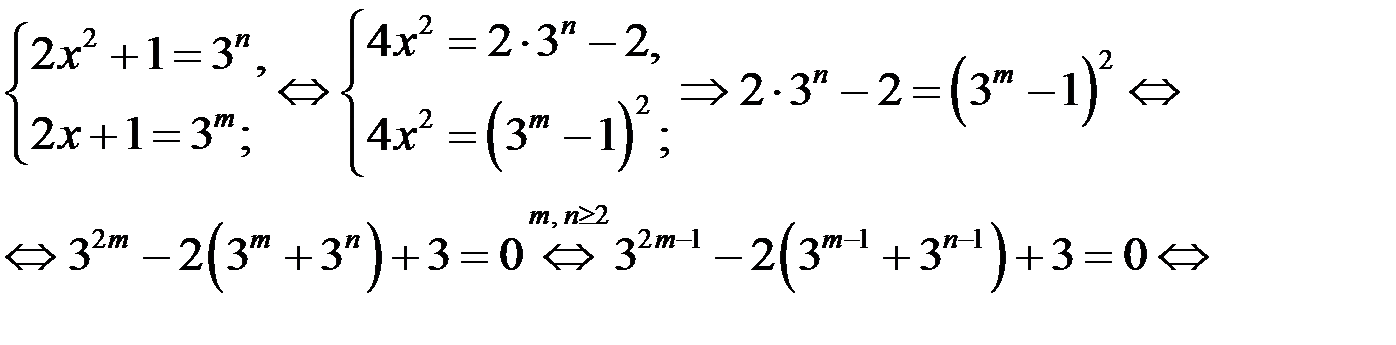
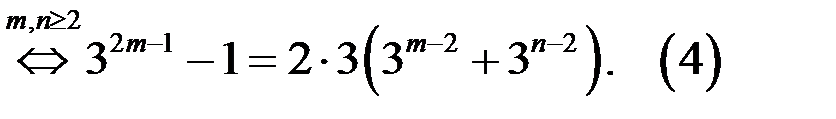
Левая часть уравнения (4) не делится на 3, а правая часть уравнения (4) делится на 3. Тогда уравнение (4), а значит и уравнение (1), не имеет решений в целых числах.
Ответ. 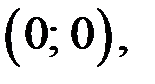
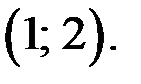
68. Решите уравнение 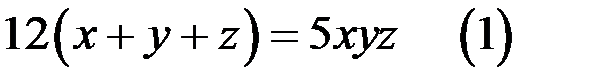 в натуральных числах.
в натуральных числах.
Решение. 1. Замечание. Так как 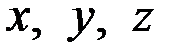 входят в уравнение симметрично, тогда, если
входят в уравнение симметрично, тогда, если 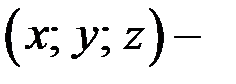 решение уравнения, то решениями этого уравнения являются также тройки чисел
решение уравнения, то решениями этого уравнения являются также тройки чисел 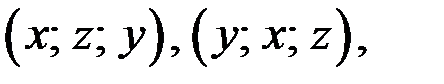
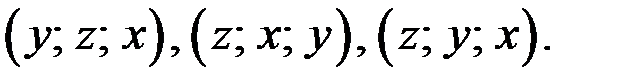
Так как 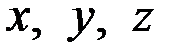 входят в уравнение симметрично, то будем считать, что
входят в уравнение симметрично, то будем считать, что 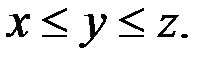 Тогда
Тогда
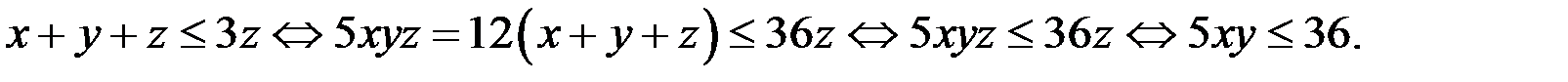
а) Оценим х.
Так как 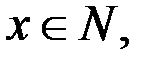 то из неравенства
то из неравенства 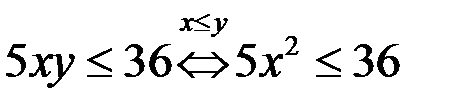 следует: что
следует: что 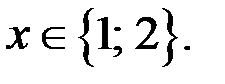
б) Оценим ху.
Имеем 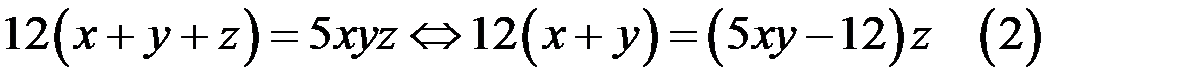
Так как 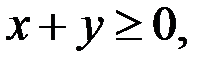 то из (2) следует, что
то из (2) следует, что 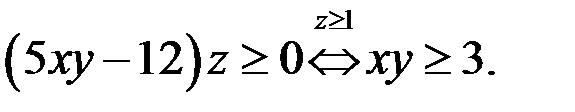
Кроме того 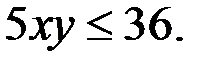 Итак, получили
Итак, получили 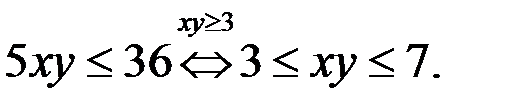
2. Найдём натуральные решения уравнения (1), если 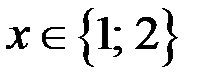 и
и 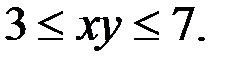
а). Если 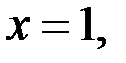 то
то 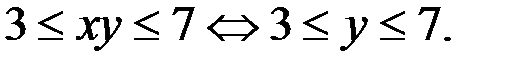 Итак,
Итак, 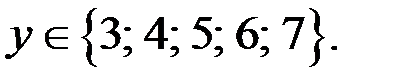
Из уравнения (3) следует, если 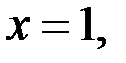 то
то 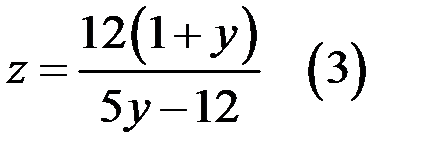
Легко проверить: так как 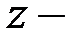 натуральное число, то только
натуральное число, то только 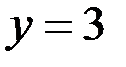 (при условии, что
(при условии, что 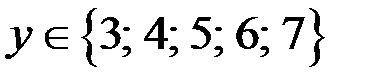 ) удовлетворяет уравнению (3). Из уравнения (3), если
) удовлетворяет уравнению (3). Из уравнения (3), если 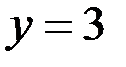 , то находим:
, то находим: 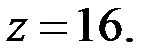 Так как
Так как 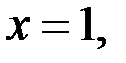
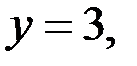
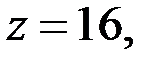 то тройка чисел
то тройка чисел 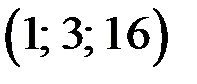 является решением исходного уравнения (1).
является решением исходного уравнения (1).
б). Если 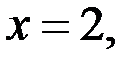 то
то 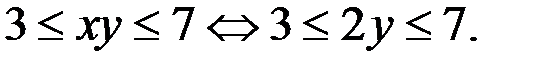 Итак,
Итак, 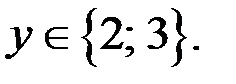
Из уравнения (2) следует, если 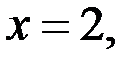 то
то 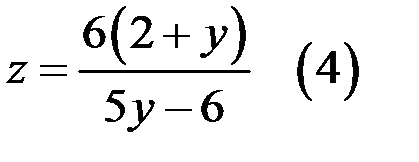
Легко проверить: так как 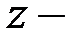 натуральное число, то только
натуральное число, то только 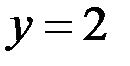 (при условии, что
(при условии, что 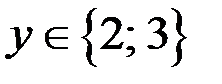 ) удовлетворяет уравнению (4). Из уравнения (4), если
) удовлетворяет уравнению (4). Из уравнения (4), если 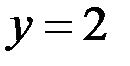 , то находим, что
, то находим, что 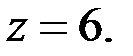 Так как
Так как 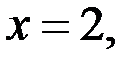
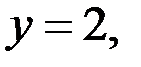
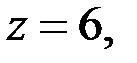 то тройка чисел
то тройка чисел 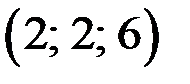 является решением уравнения (1).
является решением уравнения (1).
3. Если 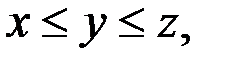 то решениями уравнения (1) являются тройки чисел
то решениями уравнения (1) являются тройки чисел 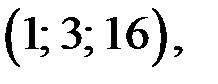
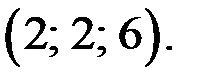 Тогда из замечания следует, что, то решениями (1) уравнения являются тройки чисел
Тогда из замечания следует, что, то решениями (1) уравнения являются тройки чисел 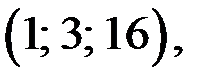
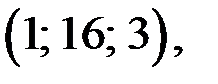
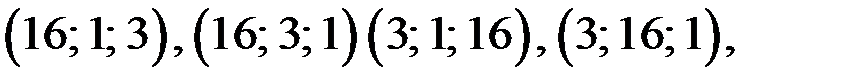
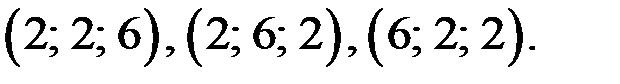
Ответ. 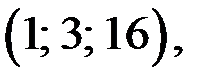
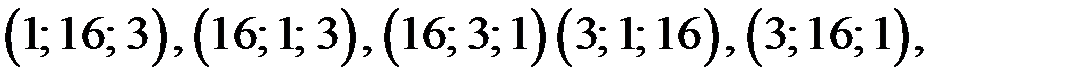
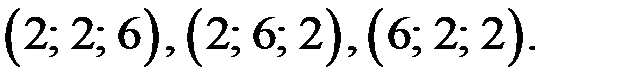
69.Найдите все натуральные решения уравнения 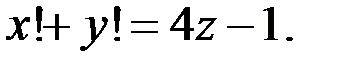
Решение. 1. Из уравнения 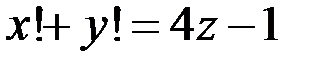 следует: так как
следует: так как 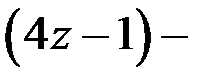 не чётное число, то и
не чётное число, то и 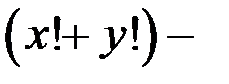 не чётное число. Это означает, что только одно из чисел
не чётное число. Это означает, что только одно из чисел 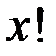 или
или 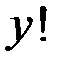 является не чётным числом. Тогда только
является не чётным числом. Тогда только 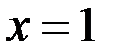 или
или 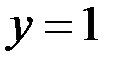 (
( 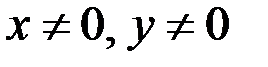 ).
).
Так как 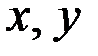 входят в уравнение симметрично, то, если тройка чисел
входят в уравнение симметрично, то, если тройка чисел 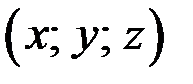 решение уравнения, то решениями этого уравнения является также тройка чисел
решение уравнения, то решениями этого уравнения является также тройка чисел 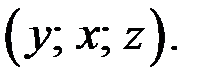
2. Пусть 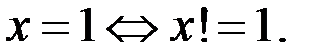 Тогда исходное уравнение принимает вид
Тогда исходное уравнение принимает вид 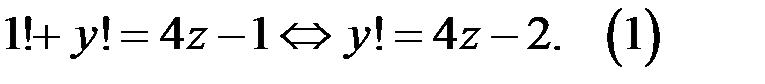 В уравнении (1) правая часть не делится на 4, тогда и левая часть не делится на 4. Это возможно только в случае, если
В уравнении (1) правая часть не делится на 4, тогда и левая часть не делится на 4. Это возможно только в случае, если 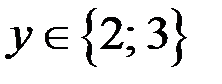 (если
(если 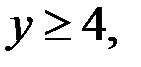 то
то 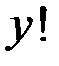 делится на 4).
делится на 4).
а) Если 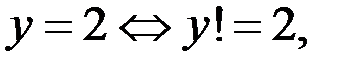 то уравнение (1) принимает вид
то уравнение (1) принимает вид 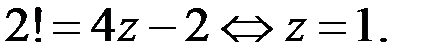 Таким образом, решением исходного уравнения является тройка чисел
Таким образом, решением исходного уравнения является тройка чисел 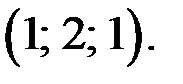
б) Если 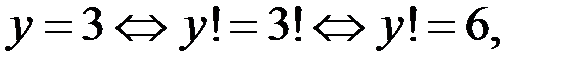 то уравнение (1) принимает вид
то уравнение (1) принимает вид 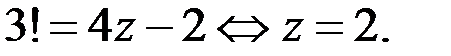 Таким образом, решением исходного уравнения является тройка чисел
Таким образом, решением исходного уравнения является тройка чисел 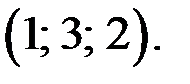
Так как 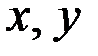 входят в уравнение симметрично, то решениями этого уравнения являются также тройки чисел
входят в уравнение симметрично, то решениями этого уравнения являются также тройки чисел 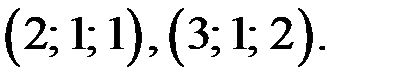
Ответ. 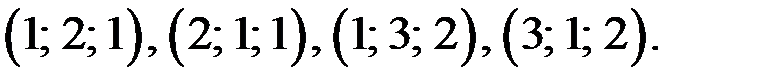
70.Найдите все целые решения уравнения
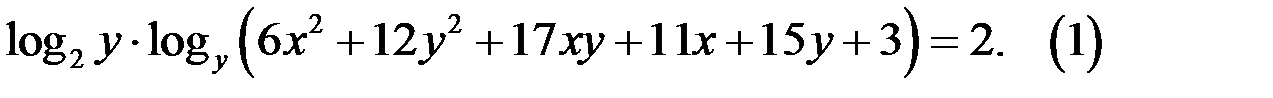
Решение. 1. Так как 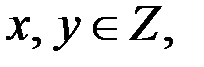 то уравнение (1) равносильно уравнению
то уравнение (1) равносильно уравнению
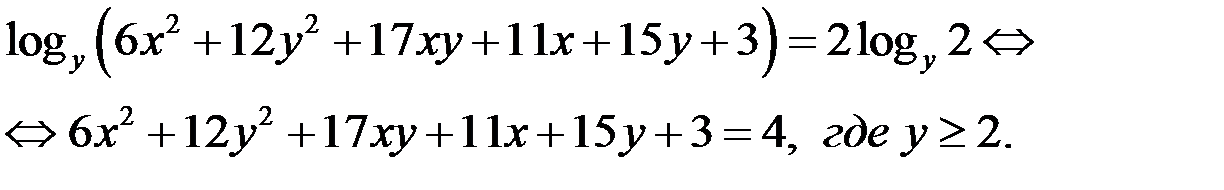
Разложим многочлен 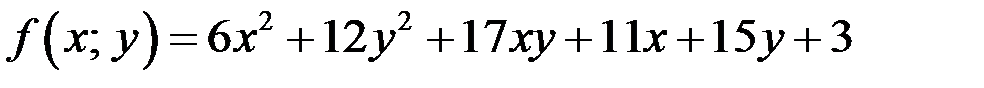 на множители. Для этого перепишем
на множители. Для этого перепишем 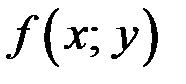 как квадратный трёхчлен относительно х. Имеем
как квадратный трёхчлен относительно х. Имеем
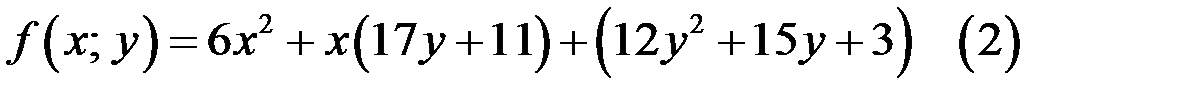
а) Найдём дискриминант 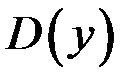 квадратного трёхчлена (2):
квадратного трёхчлена (2):
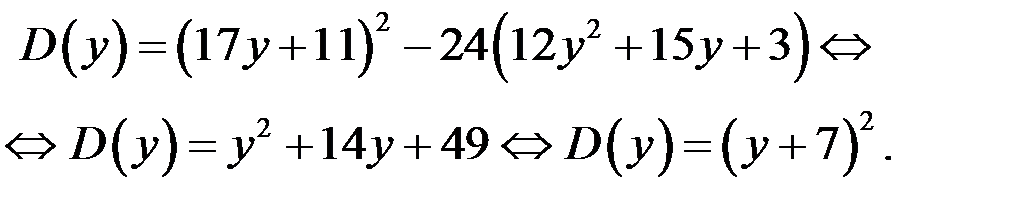
Итак, 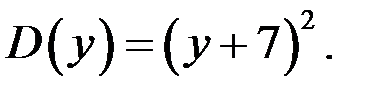
б) Найдём 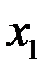 и
и 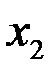 корни квадратного трёхчлена (2):
корни квадратного трёхчлена (2):
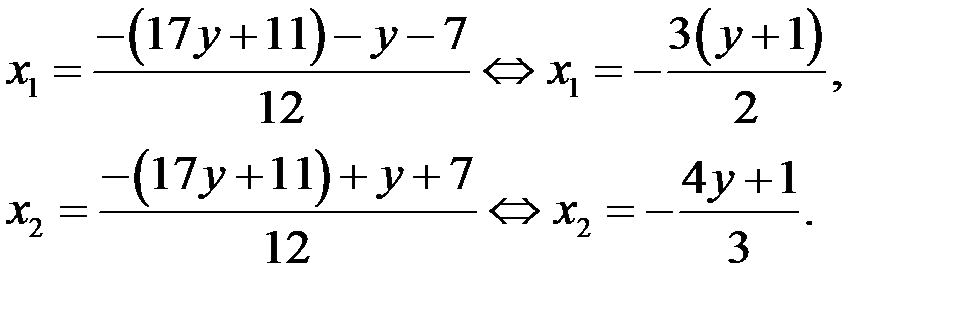
в) Найдём разложение квадратного трёхчлена (2):
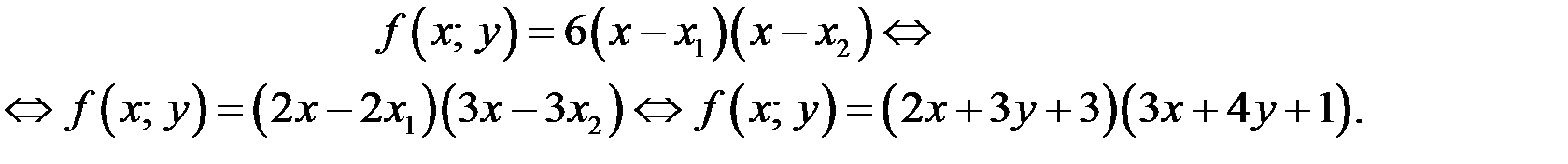 Таким образом, при любых
Таким образом, при любых 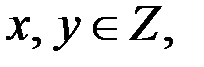 уравнение (1) равносильно уравнению
уравнение (1) равносильно уравнению 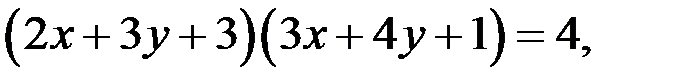 где
где 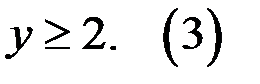
2. Найдём решение уравнение (3)
Так как 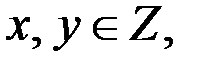 то
то 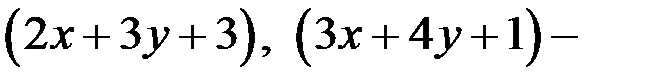 целые числа. Тогда представляем число 4 в виде
целые числа. Тогда представляем число 4 в виде
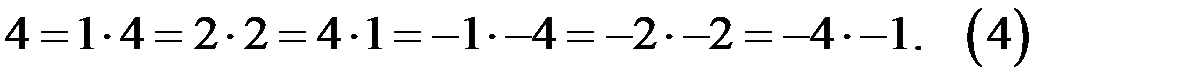
Для каждой пары 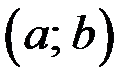 :
:
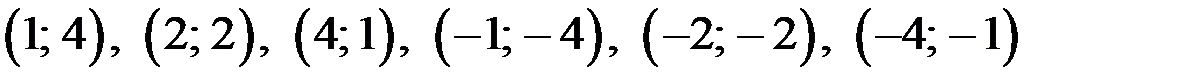
решаем в целых числах систему уравнений, где 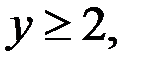
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|