
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Тригонометрические тождества. Зависимость между тригонометрическими функциями
Тригонометрические тождества
Рассмотрим произвольный прямоугольный треугольник, полученный в результате движения радиус-вектора на некоторый угол.

К прямоугольному треугольнику применима теорема Пифагора, в соответствии с которой квадрат гипотенузы будет равен сумме квадратов остальных сторон треугольника. 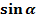 =у,
=у, 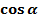 =х
=х
Так же нам известно, что гипотенуза треугольника является радиусом окружности, длина которого равна единицы, то теорему Пифагора можем получить в следующем виде:
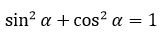
Остальные тригонометрические тождества мы можем получить, зная определение тан- генса и котангенса.
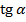 =
= 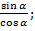
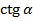 =
= 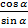
Перемножим первое и второе уравнение. В результате данного математического действия получим, что произведение тангенса на котангенс равно единице:
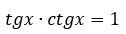
Разделив первое основное тождество почленно все на cos2α или на sin2α. В результате этого получим:
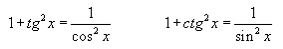
Зависимость между тригонометрическими функциями
Основное тригонометрическое тождество. Для любого угла α верно утверждение:
sin2 α + cos2 α = 1.
Эта формула связывает синус и косинус одного угла. Теперь, зная синус, мы легко найдем косинус — и наоборот. Достаточно извлечь квадратный корень:
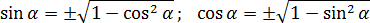
Обратите внимание на знак «±» перед корнями. Дело в том, знак функции зависит от четверти, в которой задан угол.
Задача. Найдите cos α, если известно следующее:
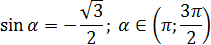
Итак, нам известен синус, а надо найти косинус. Обе эти функции есть в основном тригонометрическом тождестве. Подставляем:
sin2 α + cos2 α = 1 ⇒ 3/4 + cos2 α = 1 ⇒ cos2 α = 1/4 ⇒ cos α = ±1/2 = ±0,5.
Осталось разобраться со знаком перед дробью. Что выбрать: плюс или минус? По условию, угол α принадлежит промежутку (π 3π/2). Переведем углы из радианной меры в градусную — получим: α ∈ (180°; 270°).
Очевидно, это III координатная четверть, где все косинусы отрицательны. Поэтому cos α = −0,5.
Задача. Найдите tg α, если известно следующее:
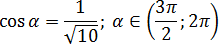
Тангенс и косинус связаны уравнением, следующим из основного тригонометрического тождества:
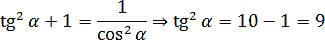
Получаем: tg α = ±3. Знак тангенса определяем по углу α. Известно, что α ∈ (3π/2; 2π). Переведем углы из радианной меры в градусную — получим α ∈ (270°; 360°).
Очевидно, это IV координатная четверть, где все тангенсы отрицательны. Поэтому tg α = −3.
Задача. Найдите cos α, если известно следующее:
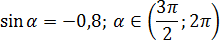
Снова известен синус и неизвестен косинус. Запишем основное тригонометрическое тождество:
sin2 α + cos2 α = 1 ⇒ 0,64 + cos2 α = 1 ⇒ cos2 α = 0,36 ⇒ cos α = ±0,6.
Знак определяем по углу. Имеем: α ∈ (3π/2; 2π). Переведем углы из градусной меры в радианную: α ∈ (270°; 360°) — это IV координатная четверть, косинусы там положительны. Следовательно, cos α = 0,6.
Задача. Найдите sin α, если известно следующее:
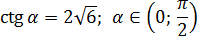
Запишем формулу, которая следует из основного тригонометрического тождества и напрямую связывает синус и котангенс:
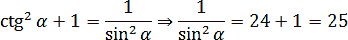
Отсюда получаем, что sin2 α = 1/25, т.е. sin α = ±1/5 = ±0,2. Известно, что угол α ∈ (0; π/2). В градусной мере это записывается так: α ∈ (0°; 90°) — I координатная четверть.
Итак, угол находится в I координатной четверти — все тригонометрические функции там положительны, поэтому sin α = 0,2.
Синус, косинус, тангенс, котангенс углов 
Точки A и C получены поворотом точки (1;0) на углы α и −α соответственно.
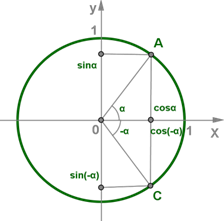
Единичная окружность
Абсциссы этих точек совпадают, а ординаты различаются только знаками, т. е. sin(−α)=−sinα и cos(−α)=cosα.
Следовательно, функция y=sinx является нечётной функцией, а y=cosx — чётной функцией.
Так как функция y=tgx=sinx/cosx, то будет верно равенствоtg(−x)=−tgx, т. е. функция y=tgx — нечётная функция, у= 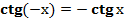
Например: 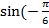 )=-
)=- 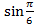 =
= 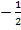
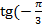 ) = -
) = - 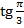 = -
= - 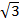
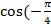 )=
)= 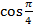 =
= 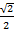
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|