
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Значения тригонометрических функций.
Значения тригонометрических функций.
| p | |||||||
| sin a | 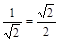
| 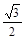
| –1 | ||||
| cos a | 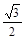
| 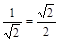
| –1 | ||||
| tg a | 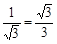
| 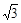
| — | — | |||
| ctg a | — | 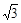
| 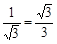
| — |
Вычислить: а) 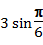 +2
+2 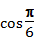 -
- 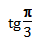 =3
=3 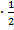 +2
+2 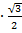 -
- 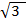 =1,5 +
=1,5 + 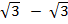 = 1,5
= 1,5
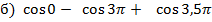 =1 -
=1 - 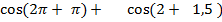 =1-
=1- 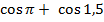 = 1 –(-1) +0= 2
= 1 –(-1) +0= 2
Знаки тригонометрических функций
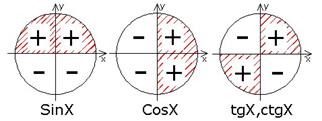
Примеры: Определите знаки тригонометрических функций и выражений (значения самих функций считать не надо):
1. sin (3π/4);
2. cos (7π/6);
3. tg (5π/3);
4. sin (3π/4) · cos (5π/6);
5. cos (2π/3) · tg (π/4);
6. sin (5π/6) · cos (7π/4);
7. tg (3π/4) · cos (5π/3);
8. ctg (4π/3) · tg (π/6).
План действий такой: сначала переводим все углы из радианной меры в градусную (π → 180°), а затем смотрим в какой координатной четверти лежит полученное число. Зная четверти, мы легко найдем знаки — по только что описанным правилам. Имеем:
- sin (3π/4) = sin (3 · 180°/4) = sin 135°. Поскольку 135° ∈ [90°; 180°], это угол из II координатной четверти. Но синус во II четверти положителен, поэтому sin (3π/4) > 0;
- cos (7π/6) = cos (7 · 180°/6) = cos 210°. Т.к. 210° ∈ [180°; 270°], это угол из III координатной четверти, в которой все косинусы отрицательны. Следовательно, cos (7π/6) < 0;
- tg (5π/3) = tg (5 · 180°/3) = tg 300°. Поскольку 300° ∈ [270°; 360°], мы находимся в IV четверти, где тангенс принимает отрицательные значения. Поэтому tg (5π/3) < 0;
- sin (3π/4) · cos (5π/6) = sin (3 · 180°/4) · cos (5 · 180°/6) = sin 135° · cos 150°. Разберемся с синусом: т.к. 135° ∈ [90°; 180°], это II четверть, в которой синусы положительны, т.е. sin (3π/4) > 0. Теперь работаем с косинусом: 150° ∈ [90°; 180°] — снова II четверть, косинусы там отрицательны. Поэтому cos (5π/6) < 0. Наконец, следуя правилу «плюс на минус дает знак минус», получаем: sin (3π/4) · cos (5π/6) < 0;
- cos (2π/3) · tg (π/4) = cos (2 · 180°/3) · tg (180°/4) = cos 120° · tg 45°. Смотрим на косинус: 120° ∈ [90°; 180°] — это II координатная четверть, поэтому cos (2π/3) < 0. Смотрим на тангенс: 45° ∈ [0°; 90°] — это I четверть (самый обычный угол в тригонометрии). Тангенс там положителен, поэтому tg (π/4) > 0. Опять получили произведение, в котором множители разных знаков. Поскольку «минус на плюс дает минус», имеем: cos (2π/3) · tg (π/4) < 0;
- sin (5π/6) · cos (7π/4) = sin (5 · 180°/6) · cos (7 · 180°/4) = sin 150° · cos 315°. Работаем с синусом: поскольку 150° ∈ [90°; 180°], речь идет о II координатной четверти, где синусы положительны. Следовательно, sin (5π/6) > 0. Аналогично, 315° ∈ [270°; 360°] — это IV координатная четверть, косинусы там положительны. Поэтому cos (7π/4) > 0. Получили произведение двух положительных чисел — такое выражение всегда положительно. Заключаем: sin (5π/6) · cos (7π/4) > 0;
- tg (3π/4) · cos (5π/3) = tg (3 · 180°/4) · cos (5 · 180°/3) = tg 135° · cos 300°. Но угол 135° ∈ [90°; 180°] — это II четверть, т.е. tg (3π/4) < 0. Аналогично, угол 300° ∈ [270°; 360°] — это IV четверть, т.е. cos (5π/3) > 0. Поскольку «минус на плюс дает знак минус», имеем: tg (3π/4) · cos (5π/3) < 0;
- ctg (4π/3) · tg (π/6) = ctg (4 · 180°/3) · tg (180°/6) = ctg 240° · tg 30°. Смотрим на аргумент котангенса: 240° ∈ [180°; 270°] — это III координатная четверть, поэтому ctg (4π/3) > 0. Аналогично, для тангенса имеем: 30° ∈ [0; 90°] — это I координатная четверть, т.е. самый простой угол. Поэтому tg (π/6) > 0. Снова получили два положительных выражения — их произведение тоже будет положительным. Поэтому ctg (4π/3) · tg (π/6) > 0.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|