Определения синуса, косинуса, тангенса и котангенса угла.

Определения синуса, косинуса, тангенса и котангенса угла.

Совместим тригонометрическую окружность (пока в том виде, в котором она у нас есть) и прямоугольный треугольник.

Что нам нужно, чтобы наш треугольник «целиком влез» в окружность?

Его гипотенуза должна быть не более единицы. Пусть же она у нас в точности будет равна единице. Совместим мы их вот так: треугольник ОАВ с центром в начале координат и гипотенузой равной единице, т.к. гипотенуза треугольника равна радиусу, т. е. 1.

Тогда по определению синуса: =АВ, и косинус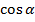а: = =ОА

Обозначим координаты точки В(х, у), тогда АВ=у, а ОА= х

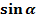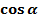=у, =х

Таким образом: В( В( ; )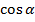

Синусом угла называется ордината точки, полученной поворотом точки (1;0) вокруг начала координат на угол (обозначается )

Косинусом угла называется абсцисса точки, полученной поворотом точки (1;0) вокруг начала координат на угол (обозначается )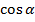

Запись В( ) показывает положение точки В на координатной окружности, а запись В(cos ;sin ) – положение той же точки на координатной плоскости.

Функция тангенс — это частное от деления функции синус на функцию косинус.

Функция котангенс — это частное от деления функции косинус на функцию синус.

Поскольку деление на нуль невозможно, функции tg и ctg определены не для всех значений аргумента. Тангенс определен лишь для значений аргумента, при которых cos ¹ 0, котангенс определен при sin t ¹ 0:

Тригонометрические функции — это общее название функций синус, косинус, тангенс и котангенс.

⇐ Предыдущая 1 234 5 Следующая ⇒