МОДЕЛИ ПРЕДЕЛЬНОГО СОСТОЯНИЯ. Модели предельного состояния в локальной области

6. МОДЕЛИ ПРЕДЕЛЬНОГО СОСТОЯНИЯ

6.1. Модели предельного состояния в локальной области

До сих пор мы рассматривали по существу законы деформирования твер-дого тела. Они являются основой инженерных расчетов, направленных на создание прочных и экономичных конструкций. При установлении условий безопасной прочности необходимо знать прежде всего условия предельного (опасного) состояния материала конструкции.

Модели схематизируют сложный процесс образования предельного состояния, зависящий от действующих напряжений и свойств материала (пластичности или хрупкости), характера нагружения и целого ряда других факторов. Они могут быть представлены в детерминированной (вполне обусловленной) или статистической (вероятностной) формах.

Принимаемые нами ограничения состоят в следующем: материал считается изотропным, нагружение предполагается простым, статическим, температура образца и окружающей среды – комнатной, не учитывается эффект длитель-ного действия нагрузки.

Предельное состояние связано с качественным изменением свойств матери-ала. Для хрупкого материала этому состоянию соответствует начало разруше-ния (появление трещин), для пластичного – появление остаточных деформа-ций. Соответственно этому предельным напряжением σ_b для хрупкого материа-ла является временное сопротивление σ_u(τ_u) для пластичного – предел текучести σ_y(τ_y).

В связи с этим требуется решить вопрос о том, на какой площадке и при каких напряжениях возникает предельное состояние в точке. В случае одноос-ного напряженного состояния или чистого сдвига этот вопрос решается опыт-ным путем. На диаграмме растяжения (сжатия, сдвига) устанавливается харак-терная точка, соответствующая предельному состоянию данного материала.

При плоском и пространственном напряженных состояниях деформирова-ние материала происходит при наличии соответственно двух или трех главных напряжений, для которых число возможных соотношений неисчерпаемо. Неисчерпаемо и число опытов, необходимых для выявления предельных значений напряжений. Проведение таких испытаний требует сложных машин и приборов, огромных затрат времени.

Указанные обстоятельства приводят к необходимости создания такой методики расчета, которая позволяла бы оценивать прочность материала при любом варианте напряженного состояния, используя результаты опытов при одноосном напряженном состоянии. При этом вводится предположение, что два каких-либо напряженных состояния считаются эквивалентными, если при пропорциональном увеличении главных напряжений в одно и то же число раз они одновременно становятся предельными. В качестве эталона (эквивалента)

принимается одноосное напряженное состояние как наиболее эксперименталь-но изученное. Предполагается, что предельное напряженное состояние лежит на границе применимости закона Гука.

Существенным элементом модели предельного состояния является принятый критерий разрушения материала или возникновения в нем состояния текучести, который считается одинаковым при всех возможных напряженных состояниях. Предполагается, что им является некоторый фактор φ, имеющий механическую природу и количественную оценку. Таким фактором может явиться, например, напряжение, деформация, удельная потенциальная энергия деформации. Значение φ, которое соответствует наступлению предельного состояния материала, будем называть предельным (опасным) и обозначать φ_b. Оно может быть определено по результатам опыта с образцом в условиях одноосного напряженного состояния или чистого сдвига.

Таким образом, условие предельного состояния материала в локальной области имеет следующее выражение:

φ = φ_b.

Его можно записать в главных напряжениях:

φ(σ₁ , σ₂, σ₃) = φ(σ_b).

При существенном влиянии скорости деформации на напряженно-деформированное состояние упомянутое условие должно содержать в качестве аргумента время.

Оценки степени удачности предложенного критерия и суждение о допустимости применения его на практике производят по результатам экспериментов с образцами, испытываемыми в условиях пространственного или плоского напряженного состояния.

В условиях предельного состояния пластичных материалов используют критерии появления пластических деформаций, рассмотренные в п. 5.6.

При пространственном напряженном состоянии возможен случай равномерного (гидростатического) растяжения (сжатия):

σ_x = σ_y = σ_z = σ.

В таком случае, исходя из критериев наибольших касательных напряжений и удельной энергии изменения формы, можно предположить, что материал должен выдерживать весьма большие (теоретически – бесконечно большие) нагрузки, так как при этом τ= 0. И если этот вывод хорошо согласуется с опытами на всестороннее равномерное сжатие, то в случае такого же рода растяжения он не соответствует физическому смыслу прочности. В связи с этим модели предельного состояния должны быть дополнены ограничениями по наибольшим растягивающим напряжениям.

Для хрупких материалов используется критерий наибольших нормальных напряжений, выдвинутый в XVII в. итальянским ученым Г.Галилеем: предельное состояние материала наступает, когда какое-либо из главных напряжений достигает величины предельного напряжения при одноосном напряженном состоянии.

Обозначив σ_bt(σ_bc) предельное напряжение на растяжение
(сжатие), запишем три случая предельного состояния:

а) если σ₁ ≥ σ₂ ≥ σ₃ ≥ 0, то σ₁ = σ_b_t;

б) если σ₁ > 0, σ₃ < 0, то σ₁ = σ_b_t, σ₃ = σ_bc;

в) если 0 ≥ σ₁ ≥ σ₂ ≥ σ₃, то σ₃ = σ_bc.

На рис.6.1 изображен квадрат, который можно рассматривать как предельный контур в случае плоского напряженного состояния в плоскости σ₁σ₃. Точки внут-ри контура образуют область, безопас-ную в отношении возникновения предельного состояния.

В то же время опыты с хрупкими ма-териалами показывают, что при сжатии предельное состояние наступает на площад- ках с наибольшими касательными напряже- Рис.6.1

ниями. Как известно, в этом случае применимо соотношение τ_b = σ_bc/2. Поэтому предельный контур во втором и четвертом квадрантах должен приниматься с учетом штриховых линий σ₃ = = σ₁ ± σ_bc.

Рассмотренные три категории предельного состояния называются классическими. К ним примыкает и критерий наибольших линейных деформаций, предложенный Э.Мариоттом и окончательно оформленный А.Сен-Венаном в середине XIX в. Этот критерий имеет лишь историческое значение, так как в силу малой согласованности с опытными данными он практически не используется.

Выявленные недостатки классических критериев потребовали от ученых поиска путей их корректировки. В 1900 г. немецкий ученый

О.Мор предложил условие предельного состояния в виде

σ₁ – mσ₃ = σ_bt,

где m = σ_bt /σ_bc. Это условие отражено штрихпунктирной линией на рис. 6.1.

При m = 1 критерий Мора совпадает с критерием наибольших касательных напряжений. Опыты, проведенные для оценки достоверности критерия Мора, дали наилучшие результаты при σ₁ > 0 и σ₃ < 0. В силу неучета влияния напряжения σ₂на возникновение предельного состояния материала в окрестности точки тела погрешности (до 17%) оказываются неминуемыми.

Ту же идею преследовал П.П. Баландин, обобщая энергетический критерий:

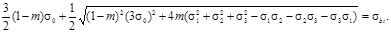
В определенном диапазоне напряженных состояний этот критерий дает удовлетворительные результаты.

Н.Н. Давиденков выдвинул идею о наличии у каждого материала двух хара-

ктеристик сопротивления – отрыву и срезу. Для хрупкого поведения их соотно-шение меньше единицы, для пластичного поведения – больше единицы. Под влиянием этой идеи Я.Б.Фридман внес на рассмотрение модель, отражающую по возможности основные факторы, влияющие на возникновение хрупкого разрушения или начала текучести, а также на разрушение вследствие среза, наступающего в конце пластической стадии работы материала. Работа над этой моделью представляется перспективной областью исследования.

При наличии концентраторов или большой изменяемости поля напряжений в критериях предельного состояния должны найти отражение не только уровни напряжений, но и их градиенты.

⇐ Предыдущая 19 20 21 22 232425 26 27 28 Следующая ⇒