
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Утверждение 7.. Утверждение 8.. Утверждение 9.. Утверждение 10.
Утверждение 7.
Пусть область определения 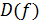 функция функция  замкнута, а сама функция – непрерывна. Тогда, она хотя бы один раз принимает все промежуточные значения между своими наибольшим и наименьшим значениями. замкнута, а сама функция – непрерывна. Тогда, она хотя бы один раз принимает все промежуточные значения между своими наибольшим и наименьшим значениями.
|
Утверждение 8.
Пусть область определения 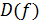 функция функция  замкнута. Тогда, если функция замкнута. Тогда, если функция  непрерывна, то она ограничена. непрерывна, то она ограничена.
|
СВОЙСТВА ФУНКЦИЙ, НЕПРЕРЫВНЫХ В ТОЧКЕ
Утверждение 9.
Пусть 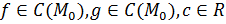 . Тогда: . Тогда:
 А если выполнено дополнительное условие
А если выполнено дополнительное условие 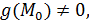 то то 
|
Утверждение 10.
Сложная функция, составленная из конечного числа непрерывных в точке  функций, непрерывна в этой точке. функций, непрерывна в этой точке.
|
Замечание: Пусть функция 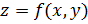 определена в окрестности точки
определена в окрестности точки  и непрерывна в этой точке.Рассмотрим функции
и непрерывна в этой точке.Рассмотрим функции 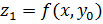 и
и 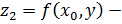 ограничения функции
ограничения функции 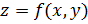 на прямые, параллельные осям координат. Получим функции одной переменной, которые, очевидно, непрерывны.
на прямые, параллельные осям координат. Получим функции одной переменной, которые, очевидно, непрерывны.
Возникает вопрос, если функция 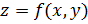 определена в окрестности точки
определена в окрестности точки  и ее ограничения на прямые, параллельные осям координат
и ее ограничения на прямые, параллельные осям координат 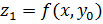 и
и 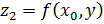 непрерывны как функции одной переменной, достаточно ли этого, чтобы сама функция
непрерывны как функции одной переменной, достаточно ли этого, чтобы сама функция 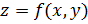 была непрерывна как функция 2 переменных? Следующий пример показывает, что данного условия недостаточно. То есть, существуют функции, непрерывные по каждому аргументу в отдельности при фиксированном втором, но не являющиеся непрерывными по совокупности переменных (это обусловлено тем, что для проверки непрерывности по совокупности переменных должно иметь место равенство:
была непрерывна как функция 2 переменных? Следующий пример показывает, что данного условия недостаточно. То есть, существуют функции, непрерывные по каждому аргументу в отдельности при фиксированном втором, но не являющиеся непрерывными по совокупности переменных (это обусловлено тем, что для проверки непрерывности по совокупности переменных должно иметь место равенство: 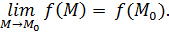 Здесь
Здесь 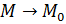 по всем возможным кривым, лежащим в области определения функции и соединяющим точки
по всем возможным кривым, лежащим в области определения функции и соединяющим точки 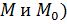 .
.
Пример 11.
Пусть 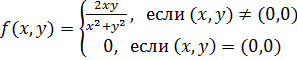 .
.
Исследовать функцию на непрерывность в точке 
Решение: Пусть  .
.
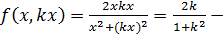 принимает все значения из отрезка
принимает все значения из отрезка 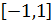 при различных
при различных 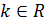 . Поэтому, пределы данной функции по различным направлениям при
. Поэтому, пределы данной функции по различным направлениям при 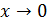 различны. Следовательно, функция не является непрерывной в начале координат.
различны. Следовательно, функция не является непрерывной в начале координат.
С другой стороны, если положить 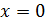 , то получим
, то получим 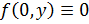 , а если положить
, а если положить 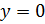 , то получим функцию
, то получим функцию 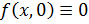 . Более того, непрерывны и функции
. Более того, непрерывны и функции 
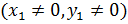 как функции одной переменной. Например
как функции одной переменной. Например 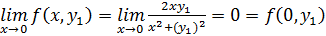 .
.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|