
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Утверждение 1.. Утверждение 2.
Утверждение 1.
Пусть функция  определена в определена в 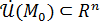 точки точки  . Если существует . Если существует 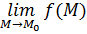 , то этот предел единственный. , то этот предел единственный.
|
Доказательство: Предположим противное.
Пусть существуют как минимум два предела: 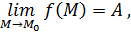
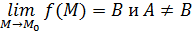 . Тогда по определению, во-первых,
. Тогда по определению, во-первых, 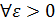
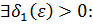
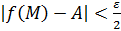 как только
как только 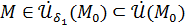 . А во-вторых, для выбранного выше
. А во-вторых, для выбранного выше 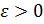

 как только
как только
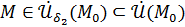 .
.
Пусть 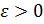 любое, но фиксировано. Ему соответствуют
любое, но фиксировано. Ему соответствуют 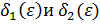 . Рассмотрим
. Рассмотрим 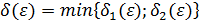 .
.
Так как 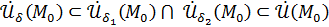 , то для всех
, то для всех 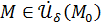 выполнены оба неравенства:
выполнены оба неравенства: 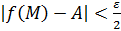 и
и  и
и
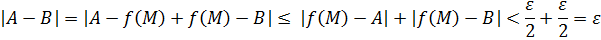
Поскольку 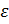 можно считать выбранным сколь угодно малым, получаем, что
можно считать выбранным сколь угодно малым, получаем, что 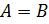 , что противоречит предположению.
, что противоречит предположению.
Таким образом, предположение о возможности существования двух различных конечных пределов функции в одной и той же точке неверно.
Следовательно, если конечный предел функции в точке существует, то он единственный.
Что и требовалось доказать.
Определение 24.
Пусть функция 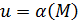 определена в определена в 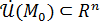 точки точки  . Функция называется бесконечно малой при . Функция называется бесконечно малой при 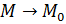 , если существует , если существует 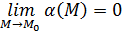
|
Утверждение 2.
Пусть функция  определена в определена в 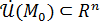 точки точки  . Если существует . Если существует 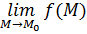 , тогда , тогда   и и 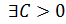 : : 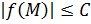 для всех для всех 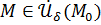 . .
|
Доказательство: Пусть выполнены условия утверждения.
Введем обозначение: 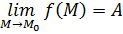 .
.
По определению предела это означает, что 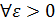
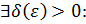
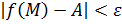 как только
как только 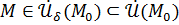 .
.
То есть, для 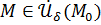 выполнено двойное неравенство:
выполнено двойное неравенство:
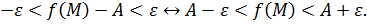
Пусть 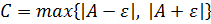 . Тогда
. Тогда 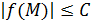 при
при 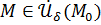 .
.
Что и требовалось доказать.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|