
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИЙ МНОГИХ ПЕРЕМЕННЫХ
ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИЙ МНОГИХ ПЕРЕМЕННЫХ
Лекция 1.
Пространство 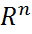 : определение, его множества. Функции нескольких переменных: определение, область определения, область значений, линии поверхности уровня, предел в точке. Непрерывность, точки разрыва. : определение, его множества. Функции нескольких переменных: определение, область определения, область значений, линии поверхности уровня, предел в точке. Непрерывность, точки разрыва.
|
ВВОДНЫЕ ОПРЕДЕЛЕНИЯ
Определение 1.
Вещественным линейным пространством  называется семейство упорядоченных групп называется семейство упорядоченных групп 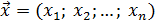 из из 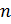 действительных чисел действительных чисел 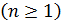 с введенными на этом множестве операциями сложения и умножения на вещественные числа: с введенными на этом множестве операциями сложения и умножения на вещественные числа:
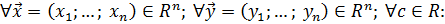 1)
1) 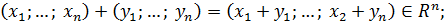 2)
2) 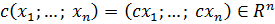
|
Замечание: Можно легко проверить, что для 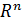 , определенного выше, выполнены все аксиомы линейного пространства и что это пространство
, определенного выше, выполнены все аксиомы линейного пространства и что это пространство 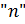 -мерно. Здесь полезно заглянуть в учебник по линейной алгебре и вспомнить аксиомы, определение
-мерно. Здесь полезно заглянуть в учебник по линейной алгебре и вспомнить аксиомы, определение 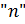 -мерного пространства и понятие базиса.
-мерного пространства и понятие базиса.
Замечание: С геометрической точки зрения 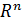 отождествляют с множеством точек
отождествляют с множеством точек 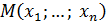 . Вещественные числа
. Вещественные числа 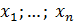 называются координатами точки
называются координатами точки 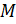 ,
,
Определение 2.
Множеством в  называется любая часть этого пространства. называется любая часть этого пространства.
|
Определение 3.
Метрическим пространством 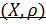 называется множество называется множество 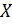 с введенной на нем метрикой (расстоянием) с введенной на нем метрикой (расстоянием) 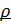 . А именно: для каждой пары точек . А именно: для каждой пары точек 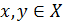 ставится в соответствие вещественное число ставится в соответствие вещественное число 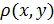 , причем выполнены следующие аксиомы. , причем выполнены следующие аксиомы. 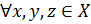 :
1) :
1) 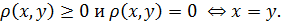 2)
2) 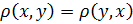 3)
3) 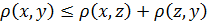
|
Замечание:с геометрической точки зрения 1) означает, что расстояние между любыми двумя точками неотрицательно и равно нулю лишь в том случае, когда точки совпадают; 2) означает, что расстояние одинаково в обе стороны, а 3), что расстояние между двумя точками не превосходит суммы расстояний от этих точек, до третьей точки (напрямую идти не длиннее, чем если заходить куда-нибудь по дороге).
Замечание:В пространстве 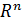 определено естественное расстояние
определено естественное расстояние 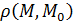 между любыми двумя точками
между любыми двумя точками 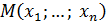 и
и 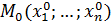 по формуле:
по формуле: 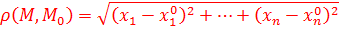 .
.
Определение 4.
Открытым шаром в 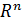 с центром в точке с центром в точке 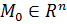 радиуса радиуса 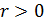 называется множество точек называется множество точек 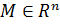 , удовлетворяющих условию: , удовлетворяющих условию: 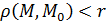 . .
|
Определение 5.
Замкнутым шаром в 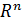 с центром в точке с центром в точке 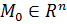 радиуса радиуса 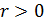 называется множество точек называется множество точек 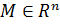 , удовлетворяющих условию: , удовлетворяющих условию: 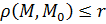 . .
|
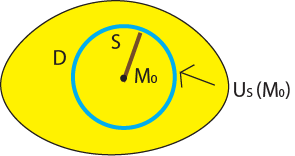
Определение 6.
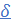 -окрестностью точки -окрестностью точки 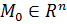 называется открытый шар радиуса называется открытый шар радиуса 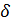 с центром в этой точке. с центром в этой точке.
|
.
Обозначение: 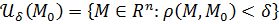 . .
|
Определение 7.
Проколотая 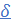 -окрестность точки -окрестность точки 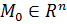 получается из получается из 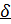 -окрестности точки -окрестности точки  после выкалывания самой точки после выкалывания самой точки  . .
|
.
Обозначение: 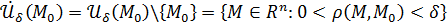
|
Определение 8.
Пусть множество 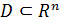 . Точка . Точка 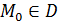 называется внутренней точкой множества называется внутренней точкой множества 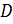 , если существует , если существует 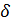 -окрестность -окрестность 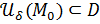 . .
|
Определение 9.
Пусть множество 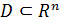 . Множество . Множество 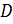 называется открытым, если все его точки внутренние. называется открытым, если все его точки внутренние.
|
Определение 10.
Пусть точка 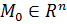 . Любое открытое множество . Любое открытое множество 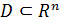 , такое, что , такое, что 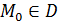 , называется окрестностью точки , называется окрестностью точки  . .
|
Обозначение: 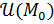 . .
|
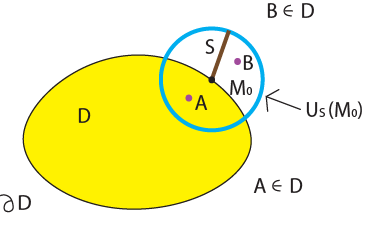
Определение 11.
Пусть множество 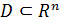 . Точка . Точка 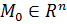 называется граничной точкой множества называется граничной точкой множества 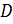 , если в любой ее окрестности , если в любой ее окрестности 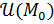 есть как точки, принадлежащие множеству есть как точки, принадлежащие множеству 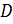 , так и точки, не принадлежащие множеству , так и точки, не принадлежащие множеству 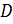 . Множество всех граничных точек . Множество всех граничных точек 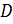 называется границей множества называется границей множества 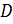 . .
|
.
Обозначение: 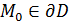 . .
|
Определение 12.
Пусть множество 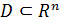 . Множество . Множество 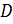 называется замкнутым, если оно содержит все свои граничные точки. называется замкнутым, если оно содержит все свои граничные точки.
|
Определение 13.
Пусть множество 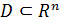 . Множество . Множество 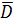 , полученное присоединением к множеству , полученное присоединением к множеству 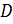 всех его граничных точек, называется замыканием множества всех его граничных точек, называется замыканием множества 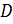 . .
|
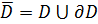 . .
|
Определение 14.
Пусть множество 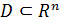 . Множество . Множество 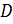 называется ограниченным, если называется ограниченным, если 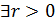 , такое что , такое что 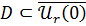 . .
|
Определение 15.
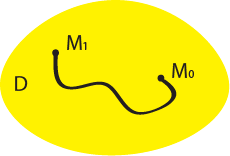
Пусть множество 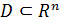 . Множество . Множество 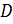 называется связным, если любые две его точки можно соединить непрерывной кривой, все точки которой принадлежат называется связным, если любые две его точки можно соединить непрерывной кривой, все точки которой принадлежат 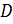 . .
|
Замечание:Пусть 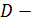 открытое множество в
открытое множество в 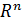 ,
, 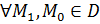 . Тогда, по определению, существует кривая
. Тогда, по определению, существует кривая 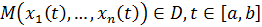 такая, что:
такая, что: 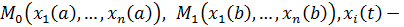 непрерывны как функции одной переменной
непрерывны как функции одной переменной 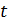 на отрезке
на отрезке 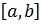 для каждого
для каждого 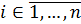 .
.
Определение 16.
Областью в 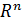 называется любое открытое связное множество называется любое открытое связное множество 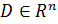 . Если . Если 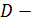 область в область в 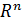 , то , то 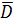 называется замкнутой областью. называется замкнутой областью.
|
Определение 17.
Область в 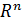 называется односвязной, если ее граница состоит из одного куска. Двусвязной, если ровно из 2 отдельных кусков, трехсвязной, если ровно из 3 и так далее. называется односвязной, если ее граница состоит из одного куска. Двусвязной, если ровно из 2 отдельных кусков, трехсвязной, если ровно из 3 и так далее.
|



ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
Определение 18.
Пусть 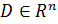 . Если любой точке . Если любой точке 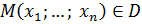 поставлено в соответствие единственное число поставлено в соответствие единственное число 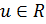 , то говорят, что на множестве , то говорят, что на множестве 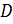 задана функция задана функция 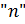 переменных: переменных: 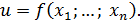
|
Определение 19.
Множество на котором функция 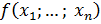 определена, называется областью определения данной функции и обозначается определена, называется областью определения данной функции и обозначается 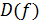 .
Множество .
Множество 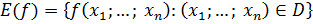 называется областью значений функции. называется областью значений функции.
|
Функции многих переменных могут быть заданы аналитически, графически или таблицей.
Самый общий метод задания функции многих переменных – аналитический. Таблицей и графиком удобно задавать функции 2 переменных.
Пример 1.
Площадь прямоугольника со сторонами 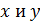 выражается формулой:
выражается формулой: 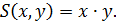
То есть, 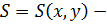 функция 2 переменных.
функция 2 переменных.
Для нее: 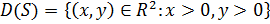 ;
; 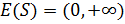 .
.
Пример 2.
Объем идеального газа выражается через функцию упругости 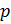 и температуру
и температуру 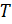 по формуле:
по формуле:
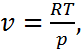
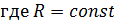 (уравнение Менделеева-Клайперона).
(уравнение Менделеева-Клайперона).
Пример 3.
Объем прямоугольного параллелепипеда со сторонами 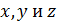 выражается формулой:
выражается формулой:
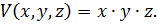
То есть, 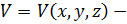 функция 3 переменных.
функция 3 переменных.
Для нее: 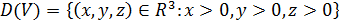 ;
; 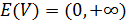 .
.
Пример 4.
Формула 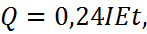
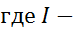 сила тока,
сила тока, 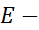 напряжение,
напряжение, 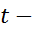 время, задает количество тепла
время, задает количество тепла 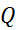 , выделенного электрическим током за время
, выделенного электрическим током за время 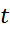 .
.
Определение 20.
Графиком функции 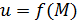 , где , где 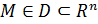 , называется множество точек , называется множество точек 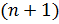 -мерного пространства, координаты которых связаны соотношением: ( -мерного пространства, координаты которых связаны соотношением: ( 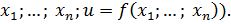
|
Замечание:с геометрической точки зрения функцию 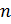 переменных можно отождествить с некоторой поверхностью в пространстве
переменных можно отождествить с некоторой поверхностью в пространстве 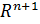 .
.
При этом, графически удобно изображать функцию 2 переменных.
Пример 5.
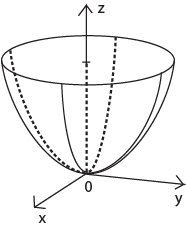
Рассмотрим функцию 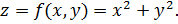
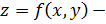 функция 2 переменных.
функция 2 переменных.
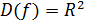 ;
; 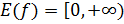 . Графиком функции является параболоид вращения в пространстве
. Графиком функции является параболоид вращения в пространстве 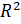 .
.
Пример 6.
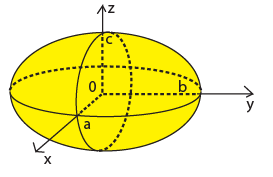
Рассмотрим функцию
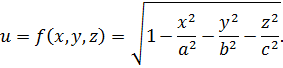
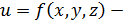 функция 3 переменных.
функция 3 переменных.
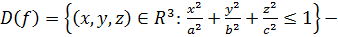 эллипсоид.
эллипсоид. 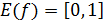 .
.
Определение 21.
Линией уровня функции 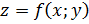 называется множество точек в называется множество точек в 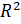 , в каждой из которых функция , в каждой из которых функция 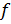 принимает одно и то же значение: принимает одно и то же значение: 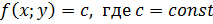 . .
|
Определение 21.
Совокупность линий уровня, соответствующих различным значениям 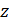 , указанным на этих линиях, называется сетью кривых функции , указанным на этих линиях, называется сетью кривых функции 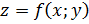
|
Замечание: сеть кривых, при условии, что она проведена для мало отличающихся друг от друга значений 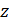 , наглядно характеризует поведение функции
, наглядно характеризует поведение функции 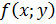 при любом изменении ее аргумента
при любом изменении ее аргумента 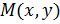 .
.
Пример 7.
Рассмотрим функцию 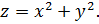 Построим для нее линии уровня:
Построим для нее линии уровня:
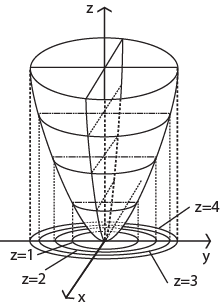
В уравнении 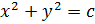 придадим
придадим 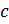 значения
значения 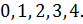
При 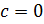 получим точку
получим точку 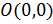 .
.
При 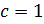 получим окружность с центром в точке
получим окружность с центром в точке 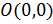 радиуса
радиуса 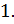
При 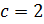 получим окружность с центром в точке
получим окружность с центром в точке 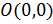 радиуса
радиуса 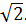
При 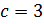 получим окружность с центром в точке
получим окружность с центром в точке 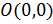 радиуса
радиуса 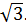
При 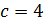 получим окружность с центром в точке
получим окружность с центром в точке 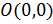 радиуса
радиуса 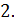
В общем случае, придадим 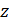 значения
значения 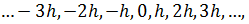 где
где 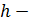 положительное число. Такая сеть функций называется равномерной. Чем быстрее изменяется функция, тем гуще сеть.
положительное число. Такая сеть функций называется равномерной. Чем быстрее изменяется функция, тем гуще сеть.
Замечание: Линии уровня применяют, например, в топографии. «Горизонталями» называют на карте линии уровня функции высоты точки над уровнем моря. В метеорологии пользуются сетями «изотерм» (линии одинаковой температуры) и «изобар» (линии одинакового давления).
Определение 22.
Поверхностью уровня функции 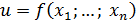 называется множество точек в называется множество точек в 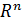 , в каждой из которых функция , в каждой из которых функция 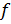 принимает одно и то же значение: принимает одно и то же значение: 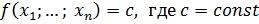 . .
|
ПРЕДЕЛ ФУНКЦИИ В ТОЧКЕ
Напомним, что проколотая окрестность точки 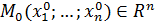 это:
это:
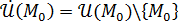 , где
, где 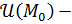 любое открытое множество, содержащее точку
любое открытое множество, содержащее точку  .
.
Проколотая 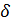 -окрестность точки
-окрестность точки  это:
это:
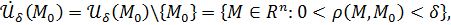 где
где 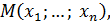 а
а
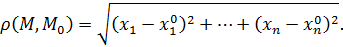
Определение 23.(конечного предела в точке)
Пусть функция  определена в некоторой проколотой окрестности определена в некоторой проколотой окрестности 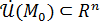 точки точки  . Число . Число 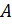 называется пределом функции называется пределом функции 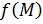 в точке в точке  , если для любого сколь угодно малого , если для любого сколь угодно малого 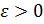 найдется такое число найдется такое число 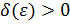 , что для всех точек , что для всех точек 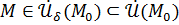 справедливо равенство: справедливо равенство: 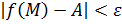 . .
|
Обозначение:
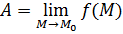 , , 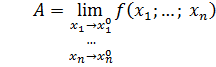 Или:
Или: 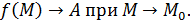
|
Замечание: В приведенном выше определении 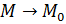 по любой кривой, лежащей в
по любой кривой, лежащей в 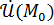 и соединяющей точки
и соединяющей точки 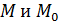 .
.
Или коротко:
Определение 23.1
Пусть функция  определена в определена в 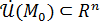 точки точки  . .
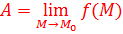 , если , если 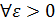 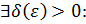 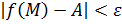 как только как только 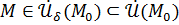 . .
|
Ниже перечислены основные свойства пределов функции в точке, аналогичные соответствующим свойствам предела для функции одной переменной. При изучении функции одной переменной, сразу после определения предела через эпсилон-дельта, было дано определение бесконечно-малой функции. Далее, были сформулированы и доказаны свойства бесконечно-малых и, уже опираясь на эти свойства, проведено доказательство свойств предела. Поскольку для функции многих переменных все эти рассуждения можно провести аналогично, ниже будет дан вывод всех вышеуказанных свойств в другом порядке. А именно, будет доказано утверждение 3 о свойствах предела с использованием только определения предела через эпсилон-дельта, а затем из них выведены свойства бесконечно-малых. Доказательства в таком порядке сложнее, но полезнее для лучшего понимания как понятия предела через эпсилон-дельта, так и собственно свойств предела функции в точке.
СВОЙСТВА КОНЕЧНЫХ ПРЕДЕЛОВ В ТОЧКЕ
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|