
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Утверждение 4.. Утверждение 5.
Утверждение 4.
Пусть функция  определена в определена в 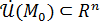 точки точки  и существует и существует 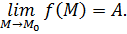 Тогда в некоторой Тогда в некоторой 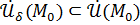 функция может быть представлена как: функция может быть представлена как: 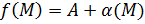 , где , где 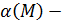 бесконечно-малая при бесконечно-малая при 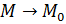 . .
|
Доказательство:
Пусть выполнены условия утверждения.
Тогда 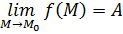 . Положим
. Положим 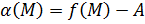 .
.
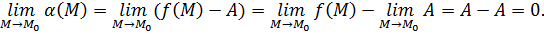
Это означает, что 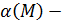 бесконечно-малая при
бесконечно-малая при 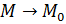 . Кроме того,
. Кроме того, 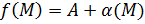 .
.
Что и требовалось доказать.
Утверждение 5.
Пусть 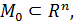 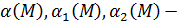 определены в определены в 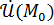 и являются бесконечно малыми функциями при и являются бесконечно малыми функциями при 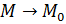 , , 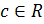 , , 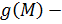 ограниченная в ограниченная в 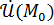 функция. Тогда: функция. Тогда:
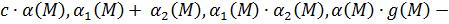 бесконечно-малые функции при бесконечно-малые функции при 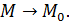
|
Доказательство: Пусть выполнены все условия теоремы.
1) Докажем, что 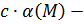 бесконечно-малая функция при
бесконечно-малая функция при 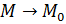 . Поскольку
. Поскольку 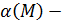 бесконечно малая при
бесконечно малая при 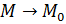 , то, по определению бесконечно-малой функции, существует
, то, по определению бесконечно-малой функции, существует 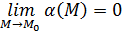
Тогда:  . А это и означает, что
. А это и означает, что 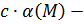 бесконечно-малая функция при
бесконечно-малая функция при 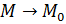 .
.
2) Докажем, что 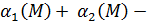 бесконечно-малая функция при
бесконечно-малая функция при 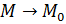 . Поскольку
. Поскольку 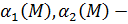 бесконечно малые при
бесконечно малые при 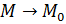 , то, по определению бесконечно-малой функции, существуют
, то, по определению бесконечно-малой функции, существуют  и
и 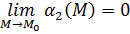
Тогда: 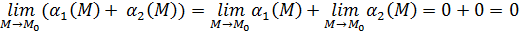 . А это и означает, что
. А это и означает, что 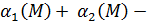 бесконечно-малая функция при
бесконечно-малая функция при 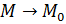 .
.
3) Докажем, что 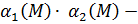 бесконечно-малая функция при
бесконечно-малая функция при 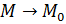 . Поскольку
. Поскольку 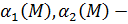 бесконечно малые при
бесконечно малые при 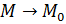 , то, по определению бесконечно-малой функции, существуют
, то, по определению бесконечно-малой функции, существуют  и
и 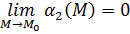
Тогда: 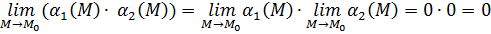 .
.
А это и означает, что 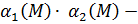 бесконечно-малая функция при
бесконечно-малая функция при 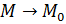 .
.
4) Докажем, что 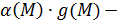 бесконечно-малая функция при
бесконечно-малая функция при 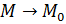 .
.
Функция 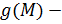 ограничена в
ограничена в 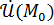 . Это означает, что
. Это означает, что 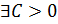 :
:  для всех
для всех 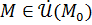 .
.
Тогда: 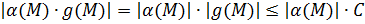 для
для 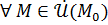 .
.
Поскольку 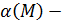 бесконечно малая при
бесконечно малая при 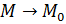 , то, по определению бесконечно-малой функции, существует
, то, по определению бесконечно-малой функции, существует 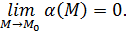 По определению предела это означает, что
По определению предела это означает, что 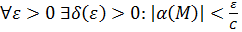 для всех достаточно близких к
для всех достаточно близких к  точек
точек 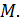
То есть, 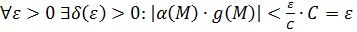 для всех достаточно близких к
для всех достаточно близких к  точек
точек 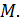
Следовательно, существует 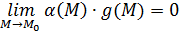 и
и 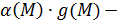 бесконечно-малая функция при
бесконечно-малая функция при 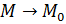 .
.
Что и требовалось доказать.
Пример 8.
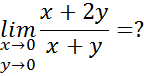
Решение:
Пусть 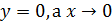 (то есть,
(то есть, 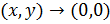 по оси
по оси 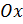 ). Тогда:
). Тогда:
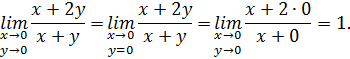
Пусть 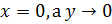 (то есть,
(то есть, 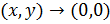 по оси
по оси 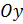 ). Тогда:
). Тогда:

Получаем разные пределы по двум разным направлениям. Значит, функция не имеет предела в точке 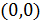 .
.
Ответ: предела не существует.
Пример 9.
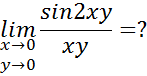
Решение:
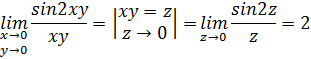
Ответ: 2.
Если точка находится на границе области определения, то используют следующее определение предела функции в точке:
Определение 23.2
Пусть функция  определена на множестве определена на множестве 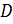 ,
где ,
где 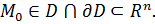
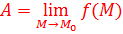 , если , если 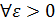 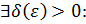 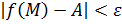 как только как только 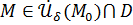 . .
|
НЕПРЕРЫВНОСТЬ ФУНКЦИИ В ТОЧКЕ
Определение 25.
Пусть функция  определена в окрестности определена в окрестности 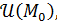 точки точки 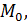 где где 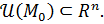 Функция Функция  называется непрерывной в точке называется непрерывной в точке  , если существует , если существует 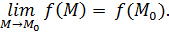 Или:
Или: 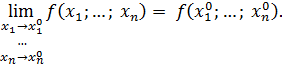
|
Обозначение: 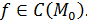
|
Определение 25.1
Пусть функция  определена на множестве определена на множестве 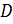 ,
где ,
где 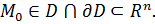 Функция Функция  называется непрерывной в точке называется непрерывной в точке  , если существует , если существует 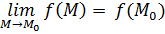 ( в смысле определения 23.2) ( в смысле определения 23.2)
|
Замечание: Если 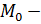 изолированная точка области определения функции
изолированная точка области определения функции  , то
, то 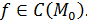 Следует из определения 25.1, так как изолированная точка принадлежит границе области определения.
Следует из определения 25.1, так как изолированная точка принадлежит границе области определения.
Замечание: Для непрерывности функции  , в точке
, в точке  необходимо выполнение 3 условий:
необходимо выполнение 3 условий:
1) 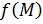 должна быть определена в какой-нибудь окрестности точки
должна быть определена в какой-нибудь окрестности точки  или же
или же  должна быть граничной точкой области определения и функция должна быть в ней определена.
должна быть граничной точкой области определения и функция должна быть в ней определена.
2) 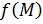 должна иметь предел, когда точка
должна иметь предел, когда точка 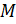 произвольно стремится к точке
произвольно стремится к точке 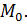
3) Этот предел должен совпадать со значением функции в точке  .
.
Определение 26.
Пусть  определена в окрестности определена в окрестности 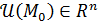 точки точки 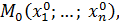 где где 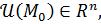 а а 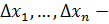 достаточно маленькие, чтобы достаточно маленькие, чтобы 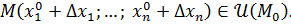 Полным приращением функции
Полным приращением функции  в точке в точке  называется: называется:
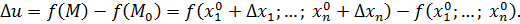
|
Замечание: Если 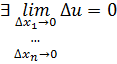 , то
, то 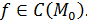
Определение 27.
Пусть функция  определена на множестве определена на множестве 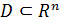 . Функция . Функция  называется непрерывной на множестве называется непрерывной на множестве 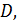 если она непрерывна в каждой точке этого множества. если она непрерывна в каждой точке этого множества.
|
Замечание: Геометрически, непрерывность функции означает, что график непрерывной функции представляет собой сплошную поверхность без разрывов. В частности, для функции 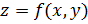 двух переменных это значит, что апликаты ее графика, соответствующие двум точкам плоскости
двух переменных это значит, что апликаты ее графика, соответствующие двум точкам плоскости 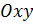 , как угодно мало отличаются друг от друга, если расстояние между этими точками достаточно мало.
, как угодно мало отличаются друг от друга, если расстояние между этими точками достаточно мало.
Определение 28.
Пусть функция  определена на множестве определена на множестве 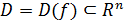 . Точка . Точка 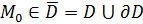 называется точкой разрыва функции называется точкой разрыва функции  , если:
1) Либо , если:
1) Либо 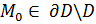 2) Либо
2) Либо 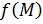 определена в некоторой окрестности определена в некоторой окрестности 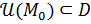 , но не является непрерывной в этой точке (соответствующий предел , но не является непрерывной в этой точке (соответствующий предел 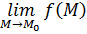 либо не существует, либо существует, но либо не существует, либо существует, но 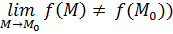 . .
|
Пример 10.
Найти точки непрерывности и точки разрыва функции 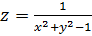 .
.
Решение: 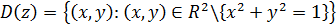 . Во всех этих точках функция непрерывна.
. Во всех этих точках функция непрерывна.
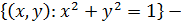 множество точек разрыва функции
множество точек разрыва функции 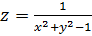 .
.
НЕКОТОРЫЕ СВОЙСТВА НЕПРЕРЫВНЫХ ФУНКЦИЙ
Замечание: Для непрерывных функций многих переменных верны теоремы, аналогичные теоремам для функций одной переменной. Ниже они приводятся без доказательства.
СВОЙСТВА ФУНКЦИЙ, НЕПРЕРЫВНЫХ НА ЗАМКНУТОМ МНОЖЕСТВЕ.
Утверждение 6.
Пусть область определения 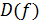 функция функция  замкнута. Тогда, если функция замкнута. Тогда, если функция  непрерывна, то она достигает своего наибольшего и наименьшего значений непрерывна, то она достигает своего наибольшего и наименьшего значений
|
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|