
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Утверждение 3.
Утверждение 3.
Пусть функции  и и 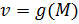 определены в определены в 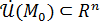 точки точки  , , 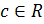 . Если существуют пределы . Если существуют пределы 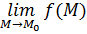 и и 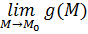 , то существуют пределы: , то существуют пределы: 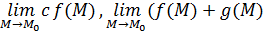 , , 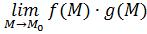 .
Если же, кроме того, если .
Если же, кроме того, если 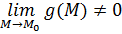 , то существует предел , то существует предел 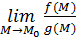 . При этом имеют место равенства: . При этом имеют место равенства:
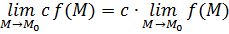
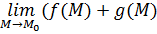 = = 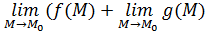
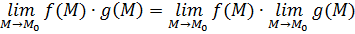
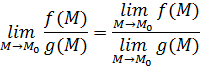
|
Доказательство: Пусть выполнены все условия теоремы.
Введем обозначения: 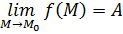 ,
, 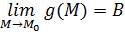 .
.
1) Докажем существование соответствующего предела и равенства
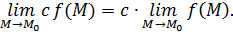
Поскольку 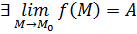 , то это означает по определению, что
, то это означает по определению, что
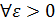
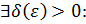
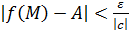 как только
как только 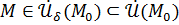 . Тогда
. Тогда 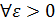
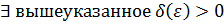 такое, что выполнено неравенство:
такое, что выполнено неравенство: 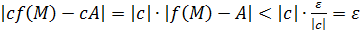 для
для 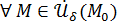 .
.
А это и означает, по определению предела, и то, что вышеуказанный предел существует, и то, что имеет место соответствующее равенство.
2) Докажем существование соответствующего предела и равенства
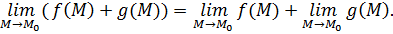
Поскольку 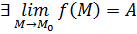 , то это означает по определению, что
, то это означает по определению, что
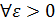
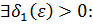
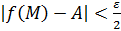 как только
как только 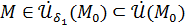 .
.
В то же время, по условию, 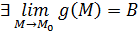 . это означает по определению, что для выбранного выше
. это означает по определению, что для выбранного выше 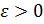
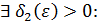
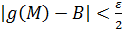 как только
как только 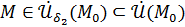 .
.
Рассмотрим 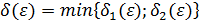 .
.
Так как 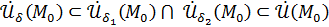 , то для всех
, то для всех 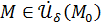 выполнены оба неравенства:
выполнены оба неравенства: 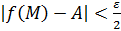 и
и 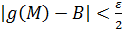 .
.
Тогда 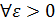 существует вышеуказанное
существует вышеуказанное 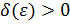 такое, что выполняется неравенство:
такое, что выполняется неравенство:
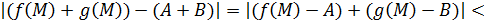
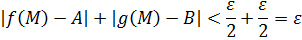
для 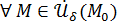 .
.
А это и означает, по определению предела, и то, что вышеуказанный предел существует, и то, что имеет место соответствующее равенство.
3) Докажем существование соответствующего предела и равенства
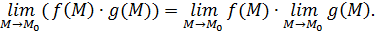
Пусть вначале 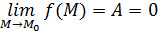 . По условию,
. По условию, 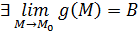 . это означает, в силу утверждения 2, что:
. это означает, в силу утверждения 2, что:
 и
и 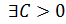 :
:  для всех
для всех 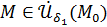 .
.
Если 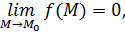 тогда по определению предела:
тогда по определению предела:
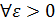
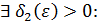
 как только
как только 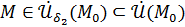 .
.
Для 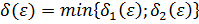 получаем, что так как
получаем, что так как 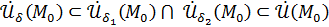 , то для всех
, то для всех 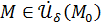 выполнены оба неравенства:
выполнены оба неравенства: 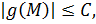
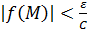 .
.
Тогда получаем:
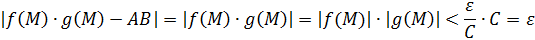
Получаем, что 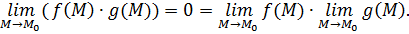
Таким образом, в этом частном случае утверждение доказано.
Пусть теперь 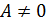 .
.
По условию, 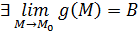 . это означает по определению, что для
. это означает по определению, что для 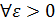
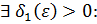
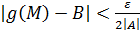 как только
как только 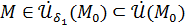 .
.
В то же время, в силу утверждения 2:
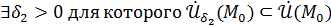 и
и 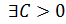 :
:  для всех
для всех 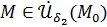 .
.
Поскольку 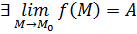 , то это означает по определению, что для выбранного выше
, то это означает по определению, что для выбранного выше 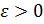
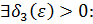
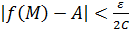 как только
как только
 .
.
Рассмотрим  .
.
Так как 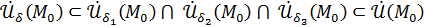 , то для всех
, то для всех 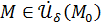 выполнены три неравенства:
выполнены три неравенства: 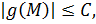
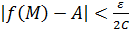 и
и 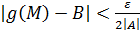 .
.
Тогда 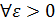 существует вышеуказанное
существует вышеуказанное 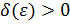 такое, что выполняется неравенство:
такое, что выполняется неравенство:
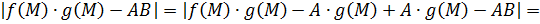
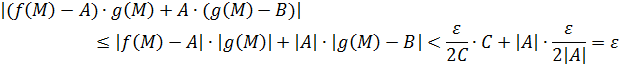
для 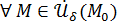 .
.
А это и означает, по определению предела, и то, что вышеуказанный предел существует, и то, что имеет место соответствующее равенство.
4) Докажем существование соответствующего предела и равенства

при условии, что 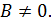
Покажем вначале, что так как 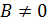 , то
, то 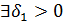 для которого
для которого  и
и 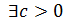 :
: 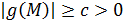 для всех
для всех 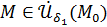 .
.
В самом деле, по определению предела для 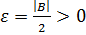
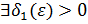 :
:
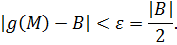
Тогда:
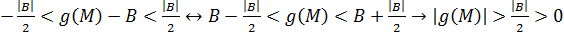
в 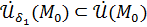 .
.
Пусть 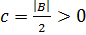 . Из вышесказанного ясно, что
. Из вышесказанного ясно, что 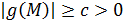 для всех
для всех 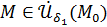 .
.
Далее, рассмотрим частный случай, когда 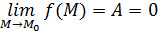 . По определению предела:
. По определению предела:
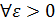
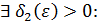
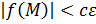 как только
как только 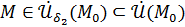 .
.
Для 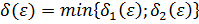 получаем, что так как
получаем, что так как 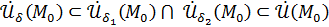 , то для всех
, то для всех 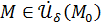 выполнены оба неравенства:
выполнены оба неравенства: 
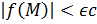 .
.
Тогда получаем:
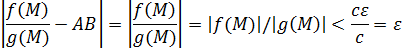
Получаем, что 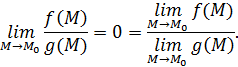
Таким образом, в этом частном случае утверждение доказано.
Пусть теперь 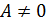 .
.
Поскольку 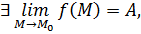 то
то 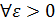
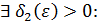
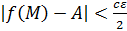 как только
как только 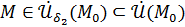 .
.
Так как 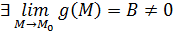 . Это означает, что для выбранного выше
. Это означает, что для выбранного выше 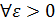
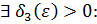
 как только
как только  .
.
Рассмотрим  .
.
Так как 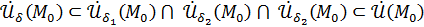 , то для всех
, то для всех 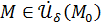 выполнены оба неравенства:
выполнены оба неравенства: 
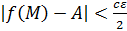 и
и  .
.
Тогда 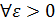 существует вышеуказанное
существует вышеуказанное 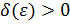 такое, что выполняется неравенство:
такое, что выполняется неравенство:
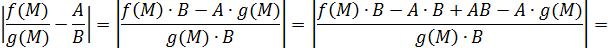
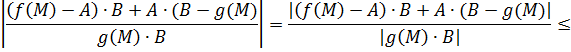
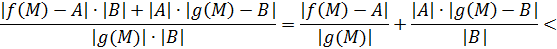
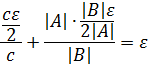
А это и означает, по определению предела, и то, что вышеуказанный предел существует, и то, что имеет место соответствующее равенство.
Утверждение полностью доказано.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|