
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Внешнее ориентирование модели.
4.4. Внешнее ориентирование модели.

Рис. 4.5. Внешнее ориентирование модели
Будем считать, что система Xф, Yф, Zф (рис.4.5)– фотограмметрическая. Например, ось Xф совпадает с базисом фотографирования. Координаты точки А известны в фотограмметрической системе. Необходимо определить ее координаты в геодезической системе XГ, YГ, ZГ.
Элементами внешнего ориентирования модели здесь являются:
- три угла Эйлера: θ, η, ξ.
- прямоугольные координаты X0, Y0, Z0 начала координат фотограмметрической системы.
- масштабный фактор t.
Если они известны, то перевычисление в геодезическую систему координат осуществляется по следующим формулам
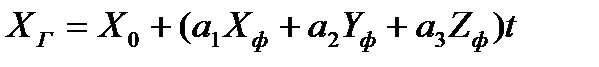
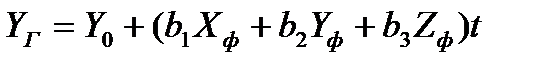 (4.13)
(4.13)
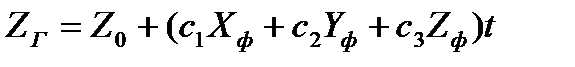 ,
,
где направляющие косинусы 
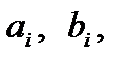
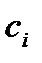 вычисляются по формуле (3.11), в которой вместо углов α, ω, κ принимаются θ, η, ξ.
вычисляются по формуле (3.11), в которой вместо углов α, ω, κ принимаются θ, η, ξ.
Поскольку обычно элементы внешнего ориентирования модели неизвестны, то для их определения запишем выражение устанавливающее связь между координатами точки фотограмметрической и геодезической систем координат.
Одна точка позволяет составить 3 уравнения вида (4.13). Для вычисления семи элементов внешнего ориентирования необходимо составить не менее семи таких уравнений. Это означает, что для решения задачи необходимо иметь 3 идентичные точки и более , координаты которых известны в обоих системах координат.
Обычно идентичных точек больше и число уравнений больше числа неизвестных. Для их решения по методу наименьших квадратов осуществляется линеаризация, т.е приведенные уравнения разлагаются в ряд Тейлора и записывается в линейном виде. Для этого задаются приближенными значениями линейных элементов преобразования из одной системы в другую X0′, Y0′, Z0′. Приближенные значения угловых элементов принимаются равными нулю. Приближенное значение масштабного фактора принимается равным единице. (t0=1).
Тогда в разложении в ряд Тейлора уравнения (4.13) можно переписать так
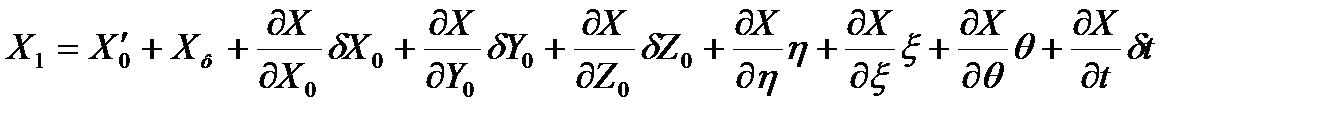
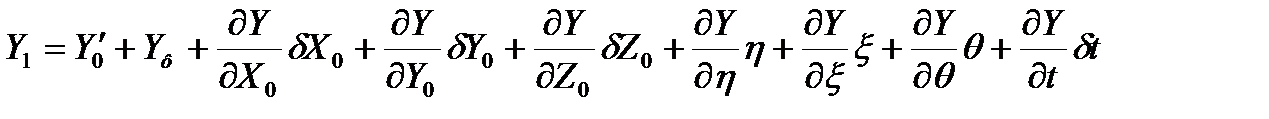 (4.14)
(4.14)
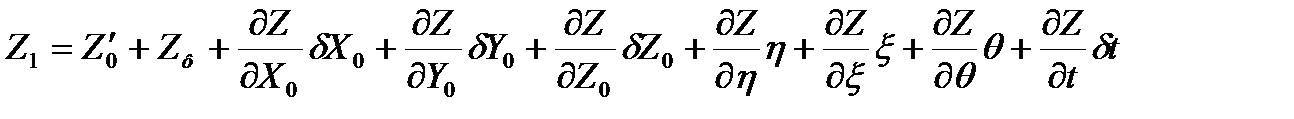
На основе такого выражения записываются уравнения поправок. При этом учитывая, что углы η, θ, ξ близкие к нулю, то настоящее уравнение можно упростить.
В первом уравнение отсутствуют: Y0, Z0.
Во втором: Х0, Z0.
В третьем: Х0, Y0.
Тогда уравнение поправок будут иметь вид:
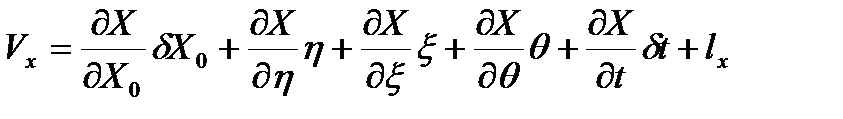
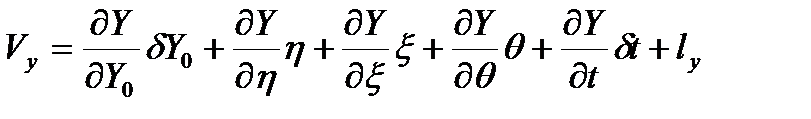 (4.15)
(4.15)
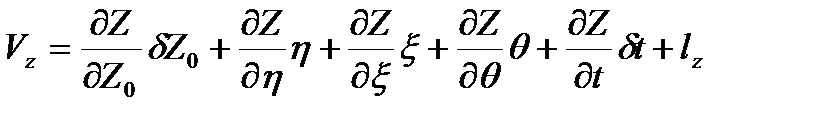
Где:


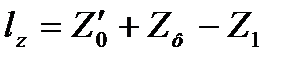
Система (4.15) решается по методу наименьших квадратов:

Находятся 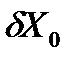 ,
,  ,
, 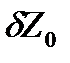 , η, ξ, θ, δt.
, η, ξ, θ, δt.
и
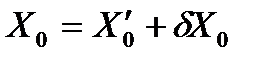

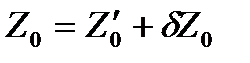
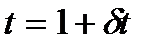
Задача решается методом приближений до тех пор, пока поправки в в определяемые элементы ориентирования не станут меньше заданной величины.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|