Фотограмметрические методы сгущения геодезической опоры.

5. Фотограмметрические методы сгущения геодезической опоры.

5.1. Теоретические основы построения аналитической аэрофототриангуляции способом связок

Для решения задачи сгущения геодезической опоры фотограмметрическим методом в способе связок составляются уравнения связи определяемых параметров и измеренных величин – параметрические уравнения поправок - на основе уравнений коллинеарности (3.18),(3.19). Их линейный вид после разложения в ряд Тейлора следующий

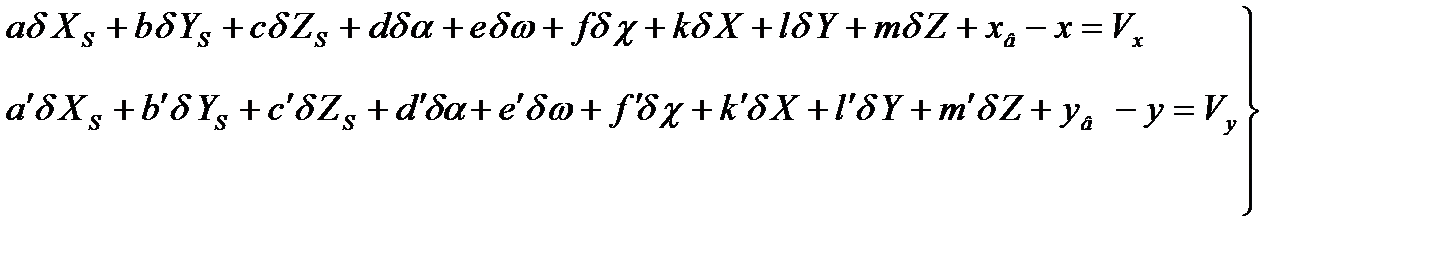(5.1)

где dX _S, dY_S , dZ_S , da, dw, dc , dX , dY, dZ – поправки к приближенным значениям неизвестных параметров:

- координатам центров проекций -X ⁰_{S ,}Y⁰ _{S ,} Z⁰_S,

- угловым элементам внешнего ориентирования a⁰ ,w⁰ ,c⁰ ,

- координатам определяемых точек Xº,Yº,Zº.

а, b,... m ^/ – частные производные от функций (3.18),(3.19). по соответствующим неизвестным;

V_x и V_Y – поправки к измеренным на снимке координатам x и y;

x _ви y_в – вычисленные по формулам(3.18),(3.19) координаты точки аэрофотоснимка при приближенных значениях неизвестных параметров:

Значения частных производных а, b,... m ^/ в (5.1) имеют следующий стандартный вид

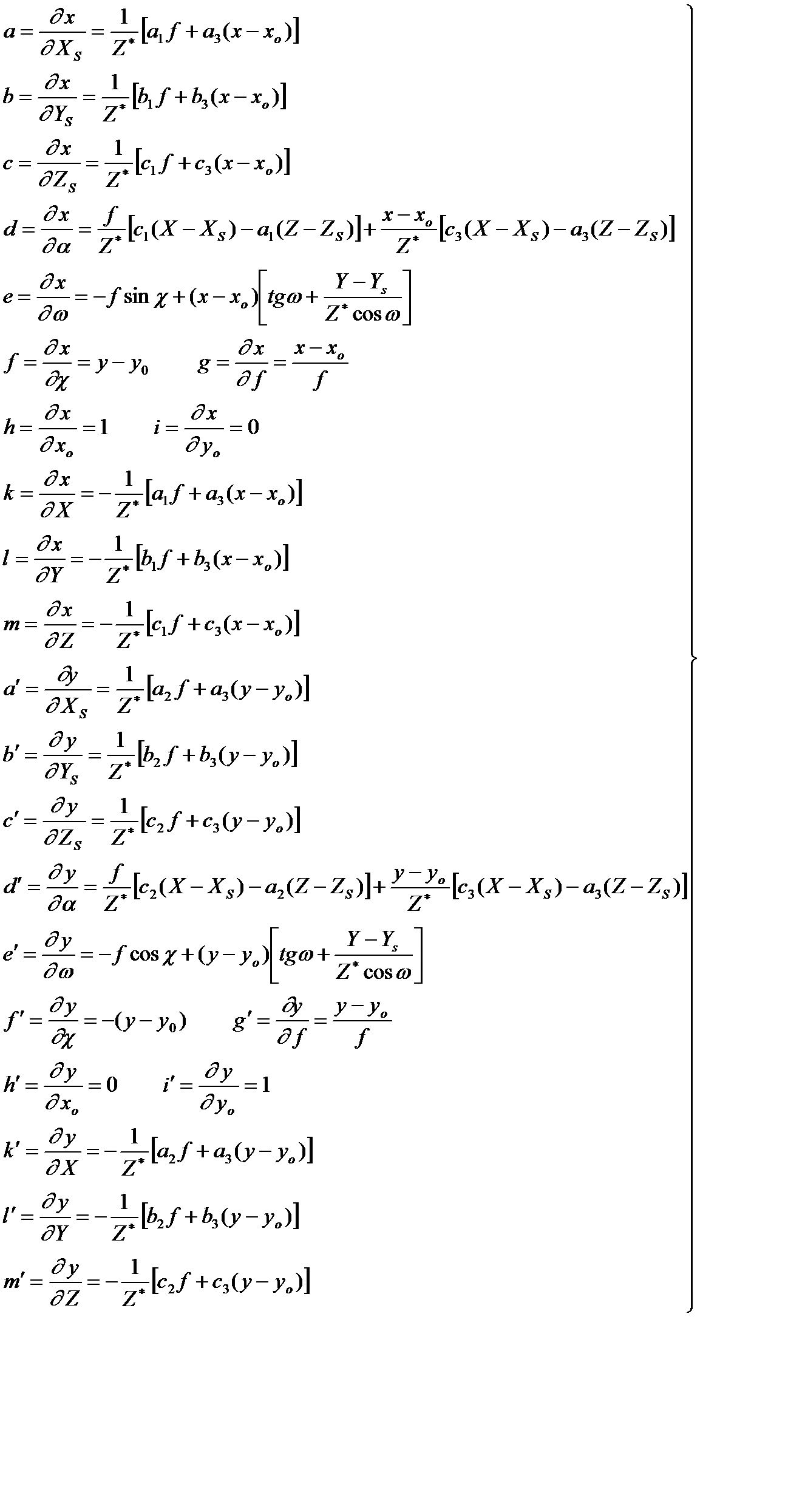(5.2)

где a_{1 ...} a_{3 ,}b_{1 ...} b_{3 ,}c_{1 ...} c₃ – значения направляющих косинусов, определяемых в соответствии с (3.10) по формулам 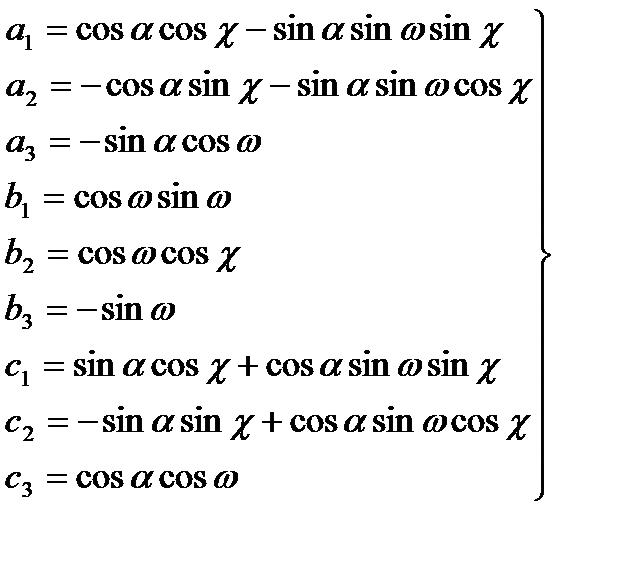( 5.3)

(5.3)

Величина 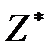определяется по формуле:

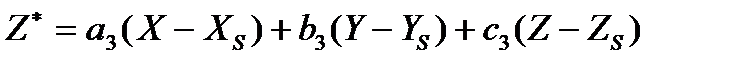. (5.4)

Отметим, что в (5.1) коэффициенты g,,h,i,g',h´,i' относятся к поправкам в элементы внутреннего ориентирования (xо,yо – координаты главной точки снимка,f – фокусное расстояние) правого и левого снимков. Однако на практике эти элементы известны и в уравнения поправок не включаются.

Уравнения (5.1) составляются для всего объекта – маршрута или блока снимков. Если

ввести матричные обозначения:

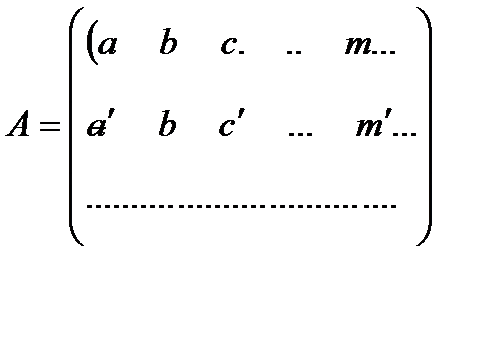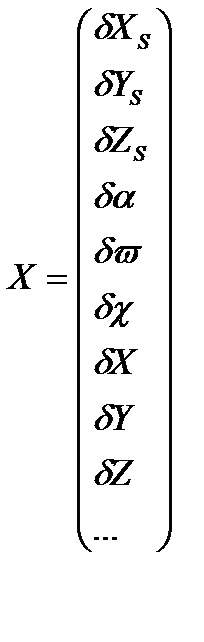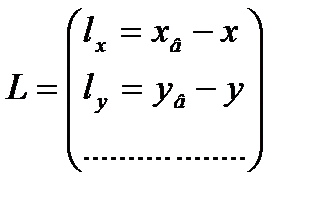
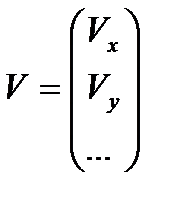то для всего объекта система уравнений (5.1) примет вид

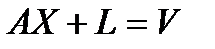(5.5)

Поскольку уравнений (5.1) всегда больше числа неизвестных параметров, то переопределенная система уравнений (5.5) решается методом максимального правдоподобия в предположении распределения ошибок измерений по нормальному закону. Такое решение в теории математической обработки геодезических измерений называется уравниванием. При этом должен достигаться минимум следующего функционала

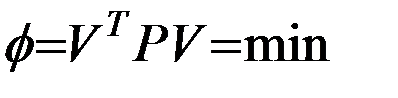где Р –весовая матрица измерений.

Минимизация такого функционала называется уравниванием по методу наименьших квадратов

Для получения решения производная 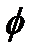по 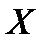приравнивается к нулю

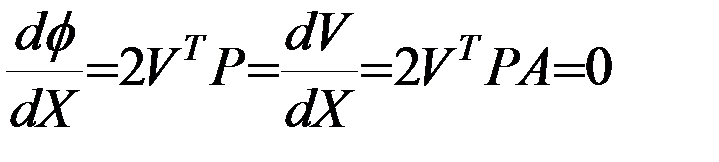или

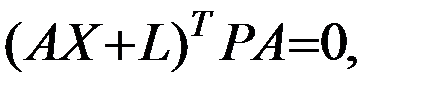
что соответствует уравнению

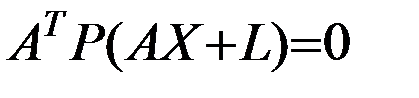После раскрытия скобок получим систему нормальных уравнений

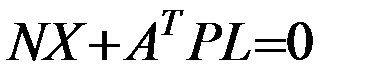, (5.6)

где

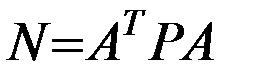. (5.7)

Из ее решения находится вектор параметров

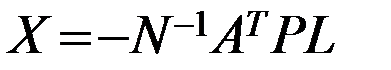(5.8)

Такое решение допустимо, если приближенные значения неизвестных параметров

достаточно точно известны. В случае, когда приближенные значения угловых ЭВО

известны с точностью до одного градуса, а координаты определяемых точек с точностью нескольких метров, решение находится методом приближений .

Следующее приближение выполняется так:

-на основе предыдущего приближения находится исправленный вектор приближенных

значений неизвестных параметров

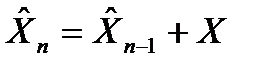, (5.9)

где 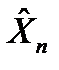, 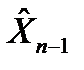- значения вектора неизвестных параметров в приближениях n и n-1

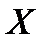- решение (5.8) в приближении n.

- с учетом новых значений вектора неизвестных параметров составляется система (5.5) и решение повторяется по алгоритму (5.6)-(5.8).

- если поправки Х в приближенные значения параметров не превосходят наперед заданной величины – приближения завершаются.

Точность вектора Х характеризуется его следующей корреляционной матрицей

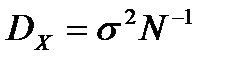, ( 5.10)

де σ – стандарт измерения, вес которого принят равным единице. Такими измерениями являются измерения координат точек на снимке. Оценкой величины σ после уравнивания является средняя квадратическая ошибка измерения, вес которого равен единице

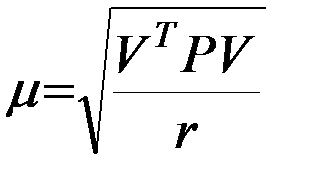(5.11)

где 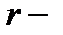число избыточных измерений в уравниваемом объекте, определяемое по

формуле

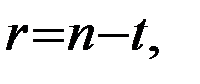(5.12)

где 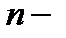число уравнений поправок, 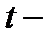число неизвестных параметров.

Диагональные элементы матрицы (5.10) являются дисперсиями параметров, полученных из уравнивания.

Дополнительно отметим, что в аэрофототриангуляции оценка точности производится и по контрольным точкам в соответствии с Инструкцией по фотограмметрическим работам при создании цифровых топографических карт и планов.- ГКИНП(ГНТА)-02-036-02-М.,ЦНИИГАиК.-2002-100с(далее просто - Инструкцией по фотограмметрическим работам) .

5.2.Пример построения аналитической аэрофототриангуляции в среде Excel. Выполнение первого приближения

⇐ Предыдущая 40 41 42 43 444546 47 48 49 Следующая ⇒