- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Эллиптические параболоиды. Конусы
5. Эллиптические параболоиды
При вращении параболы вокруг ее оси получаем параболоид вращения . Чтобы найти его уравнение, выберем прямоугольную систему координат, направив ось 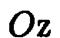 по оси вращения и совместив координатную плоскость
по оси вращения и совместив координатную плоскость 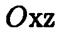 с
с
плоскостью параболы. Пусть при этом парабола описывается уравнением 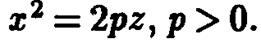 Тогда для получения уравнения поверхности вращения нужно заменить в этом уравнении
Тогда для получения уравнения поверхности вращения нужно заменить в этом уравнении  на
на 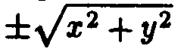 :
:
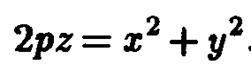
Преобразование сжатия параболоида вращения к координатной плоскости  с коэффициентом /
с коэффициентом /  дает поверхность более общего вида — эллиптический параболоид, уравнением которого будет
дает поверхность более общего вида — эллиптический параболоид, уравнением которого будет
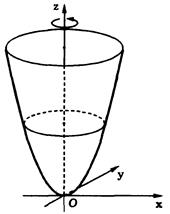
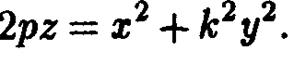 После переобозначения параметров получаем каноническое уравнение эллиптического параболоида
После переобозначения параметров получаем каноническое уравнение эллиптического параболоида
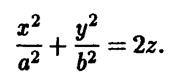
Видим, что эллиптический параболоид является поверхно
стью второго порядка. При 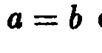 он превращается в параболоид вращения.
он превращается в параболоид вращения.
6. Конусы
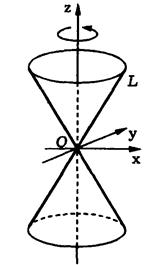
При вращении прямой 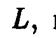 пересекающейся с осью вращения, образуется прямой круговой конус. Точка пересечения вращающейся прямой с осью вращения остается неподвижной, ее называют вершиной конуса.
пересекающейся с осью вращения, образуется прямой круговой конус. Точка пересечения вращающейся прямой с осью вращения остается неподвижной, ее называют вершиной конуса.
Как и ранее, уравнение будем выводить в прямоугольной системе координат, ось 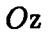 которой совпадает с осью вращения, а качало системы координат — с вершиной конуса. Ось
которой совпадает с осью вращения, а качало системы координат — с вершиной конуса. Ось 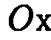 расположим так, чтобы прямая
расположим так, чтобы прямая 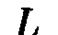 _ находилась в координатной плоскости
_ находилась в координатной плоскости 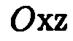 и описывалась уравнением
и описывалась уравнением 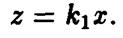 В этой системе координат
В этой системе координат
 уравнение поверхности вращения получается из уравнения прямой заменой
уравнение поверхности вращения получается из уравнения прямой заменой  на
на 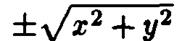 . В результате такой замены получаем
. В результате такой замены получаем 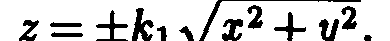
Возведя уравнение в квадрат, придем к соот
ношению 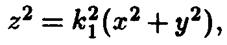 а разделив его на
а разделив его на 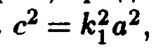 получим
получим
каноническое уравнение прямого кругового конуса
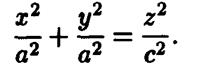
Преобразование сжатия прямого кругового конуса к координатной плоскости Охг с коэффициентом 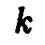 дает эллиптический конус. Его уравнение имеет вид
дает эллиптический конус. Его уравнение имеет вид
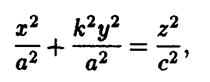
или, после переобозначения параметров,
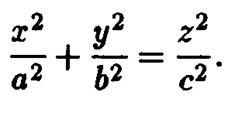
Уравнение называют каноническим уравнением эллиптического конуса. Эллиптический конус при 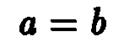 совпадает с прямым круговым конусом, и оба они являются поверхностями второго порядка
совпадает с прямым круговым конусом, и оба они являются поверхностями второго порядка
7. Метод сечений
Для выяснения формы поверхности в пространстве по ее уравнению
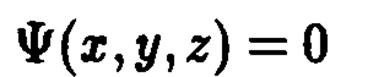
часто используют так называемый метод сечений. Он состоит в анализе пересечений поверхности с плоскостями, параллельными координатным плоскостям, например с плоскостями вида 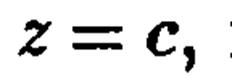 где параметр с пробегает все действительные значения. Для каждого значения с система уравнений
где параметр с пробегает все действительные значения. Для каждого значения с система уравнений
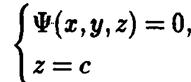
задает соответствующее пересечение. Критерием принадлежности точки 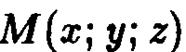 этому пересечению являются следующие условия: а)
этому пересечению являются следующие условия: а) 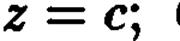 б) координаты
б) координаты 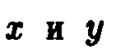 ее проекции на координатную плоскость
ее проекции на координатную плоскость 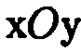 , т.е. координаты точки
, т.е. координаты точки 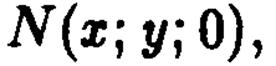 удовлетворяют уравнению
удовлетворяют уравнению
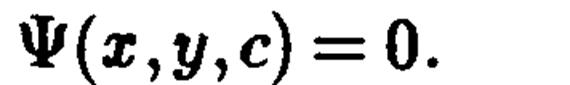
Зная эти пересечения, т.е. кривые , можно представить форму поверхности. Отметим, что указанный „рентген" поверхности можно проводить другими плоскостями, но они должны быть параллельными между собой.
Обычно при исследовании формы поверхности методом сечений используют две точки зрения на уравнение. Первая состоит в том, что его интерпретируют как уравнение проекции на координатную плоскость :  сечения. Согласно второй точке зрения предполагают, что в секущей плоскости имеется прямоугольная система координат с началом в точке
сечения. Согласно второй точке зрения предполагают, что в секущей плоскости имеется прямоугольная система координат с началом в точке  пересечения секущей плоскости с осью (
пересечения секущей плоскости с осью ( 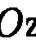 : и осями,
: и осями, 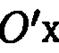 и
и 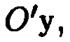 которые проектируются на соответствующие оси
которые проектируются на соответствующие оси 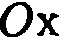 и
и
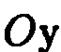 системы координат
системы координат 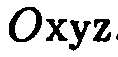 . Это позволяет говорить о
. Это позволяет говорить о
как об уравнении сечения в секущей плоскости.
Пример. В качестве примера рассмотрим уравнение эллиптического параболоида
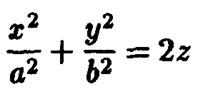
и исследуем его форму методом сечений.
Пересечение этой поверхности с плоскостью 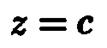 описывается уравнением
описывается уравнением
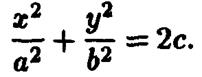
При 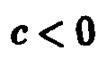 пересечение пусто, при i
пересечение пусто, при i 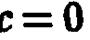 оно совпадает с началом системы координат
оно совпадает с началом системы координат 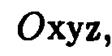 а при
а при 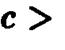 0 представляет собой эллипс
0 представляет собой эллипс
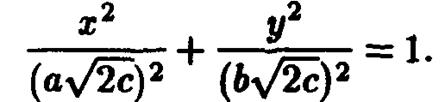
Оси этого эллипса с ростом параметра 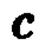 увеличиваются, и можно представить форму поверхности. Кстати, слово „эллиптический" в названии поверхности и указывает на то, что среди ее сечений имеются эллипсы.
увеличиваются, и можно представить форму поверхности. Кстати, слово „эллиптический" в названии поверхности и указывает на то, что среди ее сечений имеются эллипсы.
Пересечения этой же поверхности как с плоскостью 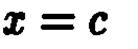 , так и с плоскостью
, так и с плоскостью 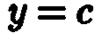 представляют собой параболы
представляют собой параболы
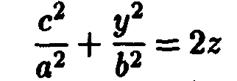
и 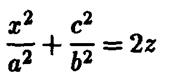
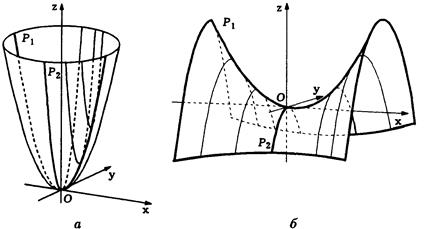
соответственно. Параболы в каждом из этих семейств сечений имеют равные параметры (они не зависят от значения с). Эти сечения позволяют дать еще одно геометрическое построение эллиптического параболоида. Рассмотрим параболу  находящуюся в плоскости
находящуюся в плоскости 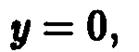 и аналогичную параболу
и аналогичную параболу 
|
|
в плоскости  " . Пусть вторая парабола
" . Пусть вторая парабола 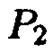
перемещается в пространстве так, что:
- вершина параболы 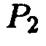 все время находится на параболе
все время находится на параболе 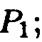
- ось параболы . 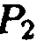 параллельна оси параболы
параллельна оси параболы 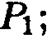
- плоскость параболы 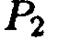 перпендикулярна плоскости параболы .
перпендикулярна плоскости параболы . 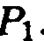 .
.
Тогда в результате такого перемещения и образуется эллиптический параболоид. При этом роли парабол  можно поменять,, т.е. перемещать параболу
можно поменять,, т.е. перемещать параболу 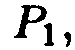 используя параболу
используя параболу 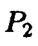 как направляющую.
как направляющую.
Уравнение
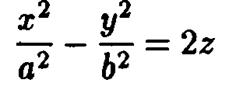
отличается от уравнения эллиптического параболоида лишь знаком одного слагаемого и тоже задает поверхность второго порядка. Ее называют гиперболическим параболоидом, а само уравнение— каноническим уравнением гиперболического параболоида.
Исследуем вид гиперболического параболоида методом сечений. Его пересечения с плоскостями 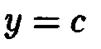 при любом значении с являются параболами:
при любом значении с являются параболами:
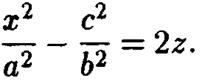
Пересечения с плоскостями 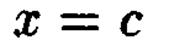 тоже при всех значениях с являются параболами:
тоже при всех значениях с являются параболами:
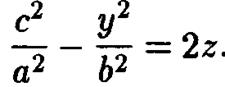
Обозначим через 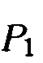 параболу, находящуюся в сечении
параболу, находящуюся в сечении 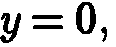 а через
а через 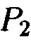 — аналогичную параболу в сечении
— аналогичную параболу в сечении 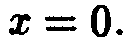 Перемещая, как и выше, параболу
Перемещая, как и выше, параболу 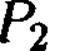 по параболе
по параболе 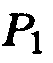 , получаем седлообразную поверхность гиперболического параболоида.
, получаем седлообразную поверхность гиперболического параболоида.
Пересечения гиперболического параболоида с плоскостями 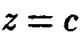 при
при 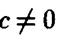 являются гиперболами
являются гиперболами
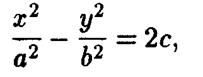
а при 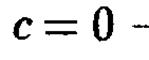 - парой пересекающихся прямых
- парой пересекающихся прямых
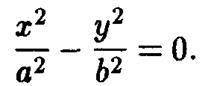
Выбор названия поверхности объясняется характером сечений: горизонтальные сечения гиперболического параболоида — это гиперболы, а два других семейства рассмотренных сечений — параболы.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|