Хелпикс

Главная

Контакты

Случайная статья



ПОВЕРХНОСТИ ВТОРОГО ПОРЯДКА. Цилиндрические поверхности.

Стр 1 из 5Следующая ⇒


§7. ПОВЕРХНОСТИ ВТОРОГО ПОРЯДКА

§1. Цилиндрические поверхности.

 

Определение. Цилиндрической называется поверхность, которую образует множество параллельных прямых (образующих), проходящих через каждую точку некоторой кривой (направляющей).

Пусть F – цилиндрическая поверхность. Выберем ДПСК так, чтобы ось  Oz была параллельна образующим. Будем считать, что направляющей служит кривая g, лежащая в плоскости  Oxy. Пусть  

                                             j(x, y) = 0 (1)

ее уравнение в плоскости Oxy (в пространстве она задается системой из двух уравнений: j(x, y) = 0 и z = 0). Пусть M(x, y, z) – произвольная точка поверхности F. Тогда ее проекция на плоскость  Oxy будет точка Mo(x, y, 0); и эта точка должна принадлежать кривой g. Поэтому ее координаты удовлетворяют (1). Но тогда этому уравнению будут удовлетворять и координаты точки M: ведь координаты x и  y у этих точек одинаковы, а z в уравнение не входит.

Итак, мы установили, что (1) и есть уравнение поверхности F, т.е. уравнение цилиндрической поверхности совпадает с уравнением ее направляющей кривой g в плоскости Oxy, если образующие параллельны оси Oz. Аналогично, если образующие параллельны Oy, то уравнение цилиндрической поверхности совпадает с уравнением направляющей кривой в плоскости Oxz.

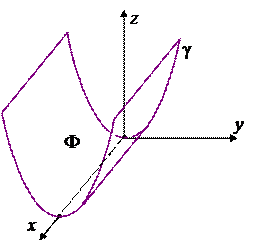И обратно, если в уравнении поверхности отсутствует, например, координата x, то сразу можем сделать вывод, что эта поверхность цилиндрическая, а ее образующие параллельны Ox.

Пример. Пусть поверхность задана уравнением y2 = 2z . Тогда это цилиндрическая поверхность, ее образующие параллельны Ox, а направляющей служит парабола

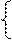                    y2 = 2z ,

                    x = 0 .

Такая поверхность называется параболический цилиндр.

Поскольку уравнение цилиндрической поверхности совпадает с уравнением направляющей кривой, то список цилиндрических поверхностей второго порядка совпадает со списком их направляющих кривых второго порядка.

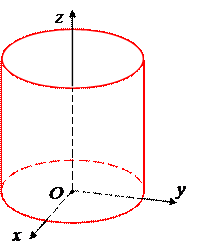
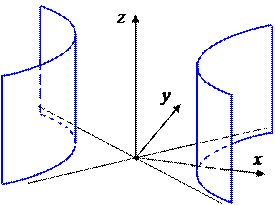
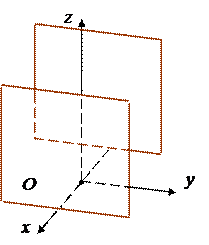
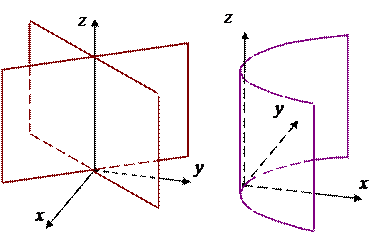
Упражнение. Самостоятельно определите, какая поверхность изображена на каждом из следующих рисунков.

 

 

1. Эллиптический цилиндр + = 1
2. Гиперболический цилиндр – = 1
3. Параболический цилиндр y2 = 2pх
4. Пара пересекающихся плоскостей a2x2 – b2 y2 = 0      
5. Пара параллельных плоскостей  x2 = a2

 

     

 

 

     
 

 

 


 

               

     

 


   

 


12345Следующая ⇒
  

© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.