
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Эллипсоиды
3. Эллипсоиды
Поверхность, которая получается при вращении эллипса вокруг одной из его осей симметрии, называют эллипсоидом вращения .Уравнение эллипсоида вращения выведем, расположив начало прямоугольной системы координат в центре эллипса и совместив ось аппликат 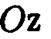 с осью вращения, а координатную плоскость
с осью вращения, а координатную плоскость 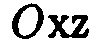 — с плоскостью эллипса . Тогда уравнение эллипса будет иметь вид
— с плоскостью эллипса . Тогда уравнение эллипса будет иметь вид
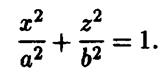
Если в этом уравнении заменить 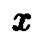 на
на 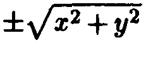 ,то
,то
получится уравнение
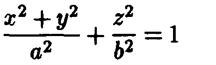
соответствующей поверхности вращения. Итак, эллипсоид вращения с осью вращения 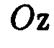 описывается уравнением
описывается уравнением
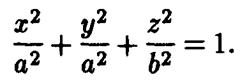
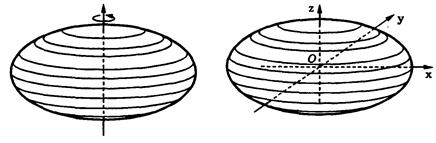
Применив к эллипсоиду вращения преобразование сжатия к координатной плоскости ' 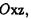 получим эллипсоид общего вида. Если
получим эллипсоид общего вида. Если 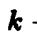 — коэффициент сжатия, то уравнение эллипсоида будет иметь вид
— коэффициент сжатия, то уравнение эллипсоида будет иметь вид 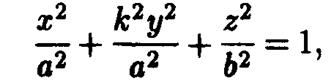
или, после переобозначения параметров,

Уравнение задает поверхность второго порядка. Его называют каноническим уравнением эллипсоида. Три параметра 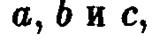 входящие в него — это полуоси эллипсоида . Если все три полуоси эллипсоида попарно различны, то эллипсоид называют трехосным.
входящие в него — это полуоси эллипсоида . Если все три полуоси эллипсоида попарно различны, то эллипсоид называют трехосным.
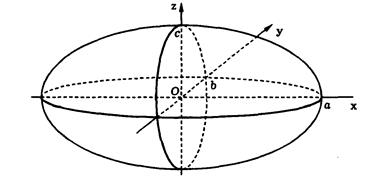
При совпадении каких-либо двух полуосей (как, например, в уравнении эллипсоид является поверхностью вращения (эллипсоидом вращения). Если равны все три полуоси ( 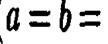
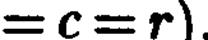 ,, то эллипсоид превращается в сферу радиуса
,, то эллипсоид превращается в сферу радиуса 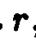 , которая описывается уравнением
, которая описывается уравнением
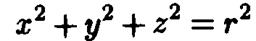
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|