Гиперболоиды

4. Гиперболоиды

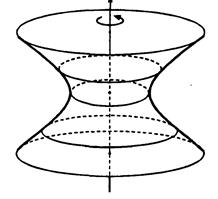
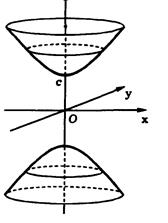
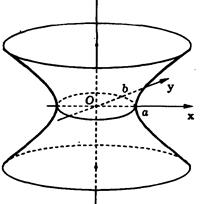
При вращении гиперболы вокруг одной из ее осей симметрии получается поверхность, называемая гиперболоидом вращения. Выбор оси вращения влияет на тип гиперболоида. Бели осью вращения является действительная ось симметрии гиперболы, то поверхность вращения будет состоять из двух частей (полостей). Это двуполостный гиперболоид вращения (. При вращении гиперболы вокруг ее мнимой оси симметрии поверхность будет состоять из одной полости. Такую поверхность называют однополостным гиперболоидом вращения.

Для вывода уравнений гиперболоидов вращения расположим прямоугольную систему координат так, чтобы ось вращения, являющаяся осью симметрии гиперболы, совпадала с осью аппликат 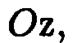а сама гипербола располагалась в координатной плоскости 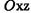с центром в начале системы координат.

Для случая двуполостного гиперболоида вращения уравнение гиперболы будет иметь вид

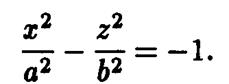
4                           *



Заменив в нем 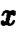на 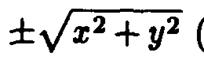,получим уравнение

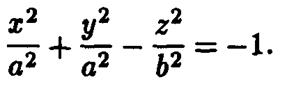
В случае однополостного гиперболоида вращения гипербола будет описываться уравнением

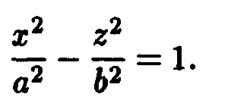
Опять меняем 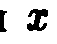на радикал : 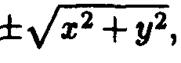получаем

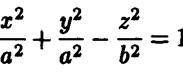I —

уравнение однополостного гиперболоида вращения.

Гиперболоиды вращения преобразованием сжатия к координатной плоскости Ош превращаются в двуполостный и однополостный гиперболоиды общего вида. При коэффициенте сжатия 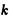их уравнениями будут соответственно

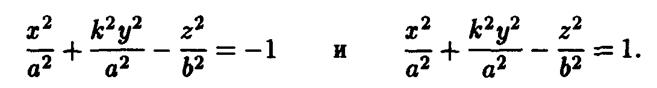
После переобозначений параметров эти уравнения преобразуются в каноническое уравнение двуполостного

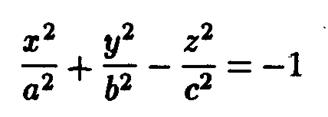  и однополостного гиперболоидов

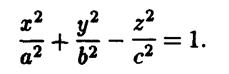  Как видно из уравнений оба гиперболоида являются поверхностями второго порядка.

             *

⇐ Предыдущая 1 2 345 Следующая ⇒